E1.4 Describe and perform translations, reflections, and rotations on a Cartesian plane, and predict the results of these transformations.
Skill: Describing and Performing Translations
Translations “slide” a shape by a given distance and direction (vector).
When shapes are transformed on a Cartesian plane, patterns emerge between the coordinates of the original and the corresponding coordinates of the image. These patterns are particularly evident when the translation vector (distance and direction) is compared to the coordinates of the original and the translated image;
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
To describe and perform an oblique (diagonal) translation, one must verify both the horizontal movement and the vertical movement. To do this, students use symbolic notation in parentheses. For example, a translation three units right and two units down is represented symbolically by (3R, 2D) or (3, 2) or (x +3, y - 2). It is best to get the students used to always describing the translation by first indicating the horizontal movement and then the vertical movement.
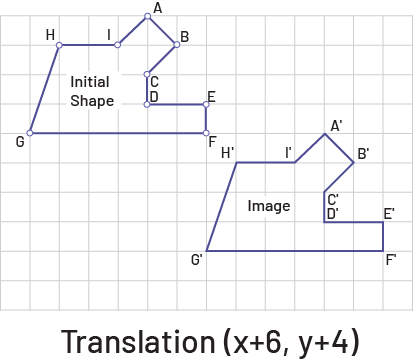
Students can describe and perform horizontal, vertical, or oblique translations defined with an arrow (translation vector). The translation vector can be placed on the shape or outside the shape. The direction of the arrow corresponds to the direction of the translation and its length corresponds to the size of the movement.

To describe and perform the translation, students must determine the magnitude of the horizontal and vertical displacements represented by the translation vector. For example, the translation vector below defines translation (-4, 2), which is a displacement of four units to the left and two units up.
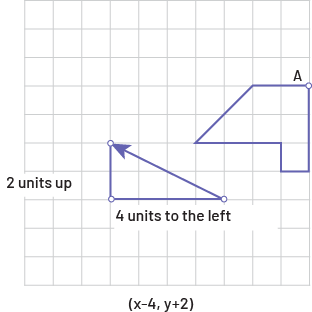
During a translation, all points of the original shape undergo the same displacement, in other words, all points of the original shape are moved in the same direction and are equidistant from the corresponding points of the image.
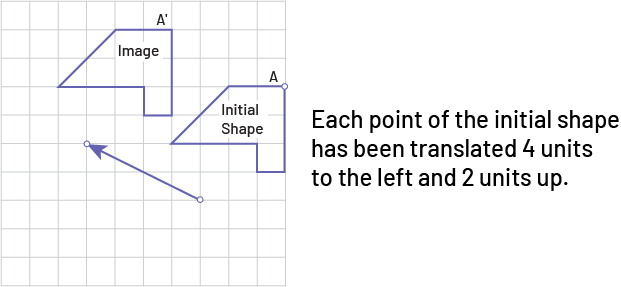 image A figure is on a grid plane. An arrow indicates the direction and length of the translation. In this case if the translation will be 2 units up and 4 units left.A second figure represents the translation. « Each point of the initial figure has undergone a translation of 4 units to the left and 2 units upwards » .
image A figure is on a grid plane. An arrow indicates the direction and length of the translation. In this case if the translation will be 2 units up and 4 units left.A second figure represents the translation. « Each point of the initial figure has undergone a translation of 4 units to the left and 2 units upwards » .
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 29-30.
Example
Draw the image of a translation of (x + 2, y - 3) of shape ABCD. Describe the effect of this translation on the coordinates of the image.
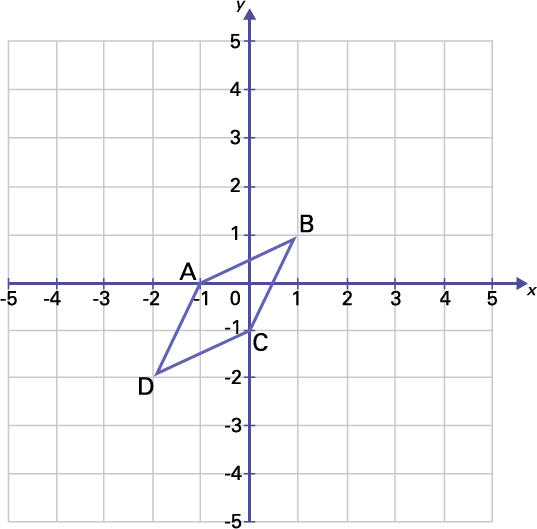 image On a Cartesian plane, the ordinate « y » is from 5 to minus 5, the abscissa « X » is from minus 5 to 5.The figure « A » « B » « C » « D » is placed on the Cartesian plane. Point « A » is at (opening parenthesis) zero, minus one (closing parenthesis), point « B » (opening parenthesis) one, one (closing parenthesis, point « C »is at (opening parenthesis) minus one, zero (closing parenthesis) And the point « D » (opening parenthesis) minus 2, minus 2 (closing parenthesis).
image On a Cartesian plane, the ordinate « y » is from 5 to minus 5, the abscissa « X » is from minus 5 to 5.The figure « A » « B » « C » « D » is placed on the Cartesian plane. Point « A » is at (opening parenthesis) zero, minus one (closing parenthesis), point « B » (opening parenthesis) one, one (closing parenthesis, point « C »is at (opening parenthesis) minus one, zero (closing parenthesis) And the point « D » (opening parenthesis) minus 2, minus 2 (closing parenthesis).
In the coordinates of the points, the value of x increases by 2 and the value of y decreases by 3.
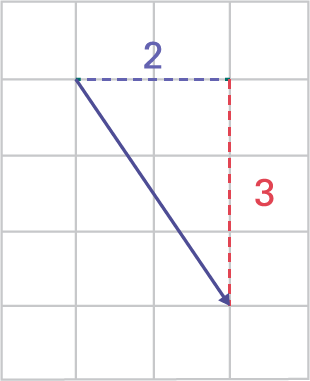
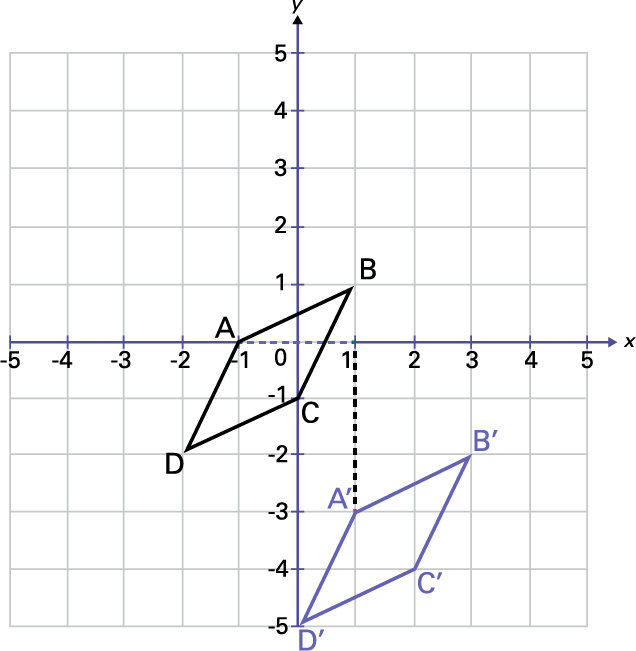 image On a Cartesian plane, the ordinate « y » is from 5 to minus 5, the abscissa « X » is from minus 5 to 5. The figure« A » « B » « C » « D » is placed on the Cartesian plane. Point « A » is at (opening parenthesis) zero, minus one (closing parenthesis), point « B » (opening parenthesis) one, one (closing parenthesis, point « C » is at (opening parenthesis) minus one, zero (closing parenthesis). And the point « D » (opening parenthesis) minus 2, negative 2 (closing parenthesis). The translation of the parallelogram is « A » prime (opening parenthesis) one, one (closing parenthesis), « B » prime (opening parenthesis) 3, minus 2 (closing parenthesis), « C » prime (opening parenthesis) 2, minus 4 (closing parenthesis), « D » prime (opening parenthesis) zero, negative 5 (closing parenthesis).
image On a Cartesian plane, the ordinate « y » is from 5 to minus 5, the abscissa « X » is from minus 5 to 5. The figure« A » « B » « C » « D » is placed on the Cartesian plane. Point « A » is at (opening parenthesis) zero, minus one (closing parenthesis), point « B » (opening parenthesis) one, one (closing parenthesis, point « C » is at (opening parenthesis) minus one, zero (closing parenthesis). And the point « D » (opening parenthesis) minus 2, negative 2 (closing parenthesis). The translation of the parallelogram is « A » prime (opening parenthesis) one, one (closing parenthesis), « B » prime (opening parenthesis) 3, minus 2 (closing parenthesis), « C » prime (opening parenthesis) 2, minus 4 (closing parenthesis), « D » prime (opening parenthesis) zero, negative 5 (closing parenthesis).
Original shape → image
(x, y) → (x + 2, y - 3)
A (-1, 0) → A' (1, -3)
B (1, 1) → B' (3, -2)
C (0, -1) → C' (2, -4)
D (-2, -2) → D' (0, -5)
I notice that the translation “slides” the original shape a given distance and is congruent to the original shape. I also notice that when there is a translation to the right, the x-value increases and when there is a translation downward, the y-value decreases.
Source: translated from En avant les maths 7e année, CM, Sens de l’espace, p. 8-9.
Skill: Describing and Performing Reflections
A reflection “flips” a shape across a reflection line to create a mirror image.
When shapes are transformed on a Cartesian plane, patterns emerge between the coordinates of the original and the corresponding coordinates of the image. These patterns are particularly evident when a shape is reflected across the x-axis or the y-axis.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
A reflection over a line is a transformation in which each point of the original shape has an image shape that is the same distance from the line of reflection as the original point but is on the opposite side of the line. The reflection causes a change in the original position and orientation of a shape, but the reflected image is congruent to the original. In other words, the reflected image is the same size and shape, but it will be “facing” a different direction, and will be in another position. It is important to note that the reflection line can be drawn in any direction relative to the original shape – horizontally, vertically, or diagonally at any angle.
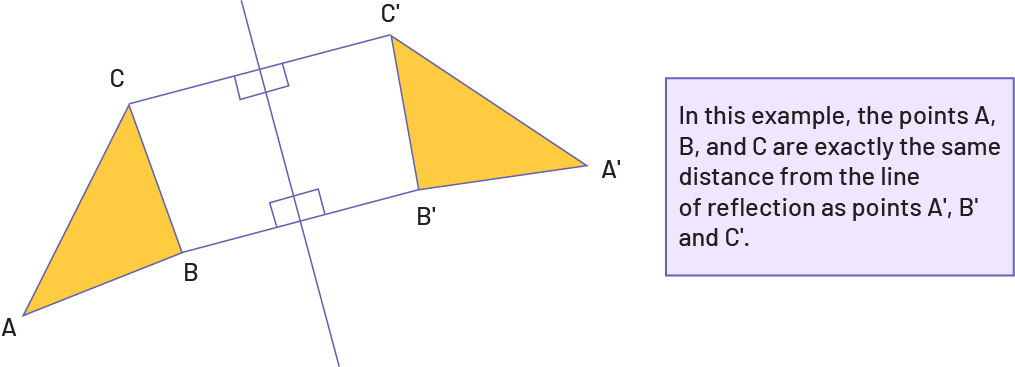 image A triangle « A » « B » « C » and its reflection, « A » prime, « B » prime, « C » primes. Think lines were placed between « C » and « C » prime, and between « B » and « B » prime.The axis of reflection is perpendicular to these two lines.In a box, we can read: In this example, the points « A », « B » , « C » are exactly at the same distance from the axis of reflection as the points « A » prime, « B » prime, et « C » primes.
image A triangle « A » « B » « C » and its reflection, « A » prime, « B » prime, « C » primes. Think lines were placed between « C » and « C » prime, and between « B » and « B » prime.The axis of reflection is perpendicular to these two lines.In a box, we can read: In this example, the points « A », « B » , « C » are exactly at the same distance from the axis of reflection as the points « A » prime, « B » prime, et « C » primes.
Source: Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 35.
Example
a) Make a reflection of the ABC triangle in the x-axis.
Describe the effect of this reflection on the coordinates of the image.
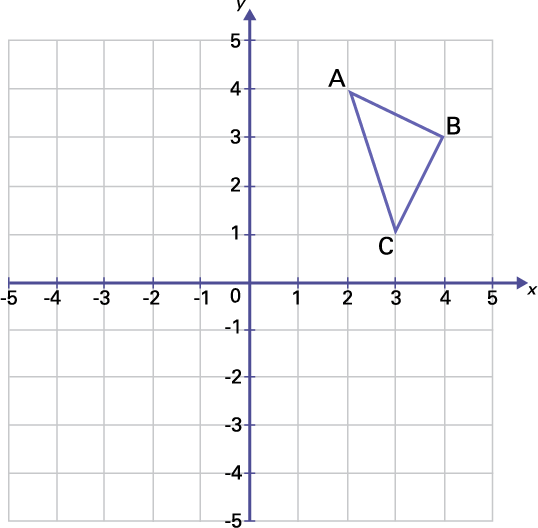 image A triangle « A » « B « C » is placed on a Cartesian plane at the following coordinates. « A » (open parenthesis) 2, 4 (close parenthesis), « B » (open parenthesis)4, 3 (close parenthesis), « C » (open parenthesis) 3, one (close parenthesis)
image A triangle « A » « B « C » is placed on a Cartesian plane at the following coordinates. « A » (open parenthesis) 2, 4 (close parenthesis), « B » (open parenthesis)4, 3 (close parenthesis), « C » (open parenthesis) 3, one (close parenthesis)
Reflection in the X-Axis
Note: When the student discovers and approaches the different transformations, it is important that they can see the relationships between the different transformations. Here are some questions to get the student to make connections.
- What do you notice about the image of the transformation?
- Are there other transformations that would allow you to obtain the same image?
- Which one do you think is the most effective? Why or why not?
In the coordinates of the points, the value of y becomes the opposite (changes sign), while the value of x remains the same.
Original shape → image
(x, y) →(x, -y)
A (2, 4) → A' (2, -4)
B (4, 3) → B' (4, -3)
C (3, 1) → C' (3, -1)
I notice that the reflection “flips” the original shape in the x-axis. I observe that even if the shape A'B'C' no longer has the same coordinates, the reflection has reproduced a figure congruent with the original shape.
b) Make a reflection of the ABC triangle in the y-axis. Describe the effect of this reflection on the coordinates of the image.
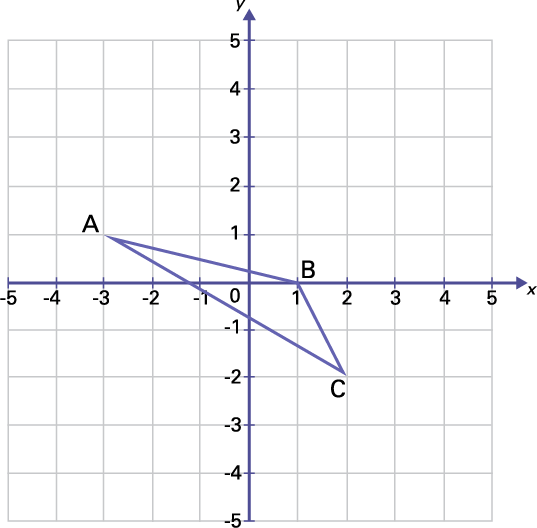 image A triangle « A » « B « C » is placed on a Cartesian plane at the following coordinates. « A » (opening parenthesis) minus 3, one (closing parenthesis), « B » (opening parenthesis) one, zero (closing parenthesis), « C » (opening parenthesis) 2, negative 2 (closing parenthesis)
image A triangle « A » « B « C » is placed on a Cartesian plane at the following coordinates. « A » (opening parenthesis) minus 3, one (closing parenthesis), « B » (opening parenthesis) one, zero (closing parenthesis), « C » (opening parenthesis) 2, negative 2 (closing parenthesis)
Reflection in the Y-Axis
In the coordinates of the points, the value of x becomes the opposite (changes sign), while the value of y remains the same.
Original shape → image
(x, y) →(-x, y)
A (-3, 1) → A' (3, 1)
B (1, 0) → B' (-1, 0)
C (2, -2) → C' (-2, -2)
I notice that the reflection “flips” the original shape in the y-axis. I observe that even if the shape A'B'C' no longer has the same coordinates, the reflection has reproduced a figure congruent with the original shape.
Source: translated from En avant les maths!, 7e année, CM, Sens de l’espace, p. 10-13.
Skill: Describing and Performing Rotations up to 360°
Rotations “turn” a shape around a centre of rotation by a given angle.
When shapes are transformed on a Cartesian plane, patterns emerge between the coordinates of the original and the corresponding coordinates of the image. These patterns are particularly evident when a shape is rotated by 90° or 180° around the origin (0, 0).
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
To describe and perform a rotation, one must understand and state:
1. the location of the center of rotation (for example, a point on the outline of the shape, inside the shape, or outside the shape);
2. angle or fraction of rotation;
3. the direction of rotation (namely, clockwise, counterclockwise).
Students need to understand what a quarter, half, and three-quarter turn clockwise or counterclockwise represents, and it is important to introduce them to a variety of kinesthetic activities that help them develop this understanding.
Using the clock (for example, a cardboard clock with two hands attached with a brad) is also an effective strategy to help students develop a sense of fractional turns. They first place the hands at 12. To represent a rotation of a quarter turn clockwise, they move the minute hand to 3. The hour hand represents the initial direction, while that of the minutes represents the direction after the rotation.
Students can make the connection between the fraction of a revolution of the large hand of a clock, the number of minutes and the number of degrees. For example, a rotation of a quarter turn of the large hand corresponds to 15 minutes or 90°.
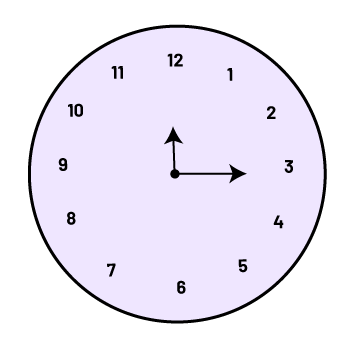
\(15 \ minutes = \frac{1}{4} \ turn = \frac{1}{4} \times 360^{\circ} = 90^{\circ}\)
Note: On a real clock, this correspondence is not quite exact since the hour hand moves slightly when the minute hand makes a rotation of a quarter turn.
It should be noted that there is still ¾ of a turn, or 45 minutes, to be made for the large hand located on the 3 to reach the 12.
\(45 \ minutes = \frac{3}{4} \ turn = \frac{3}{4} \times 360^{\circ} = 270^{\circ}\)
Once again, it is important to vary the initial direction of the hands. For example, teachers can set both hands of the clock to 2 and have students rotate clockwise half a turn. They can then understand that a half-turn rotation of the large hand corresponds to 180° or 30 minutes to determine that the minute hand should be placed at 8.
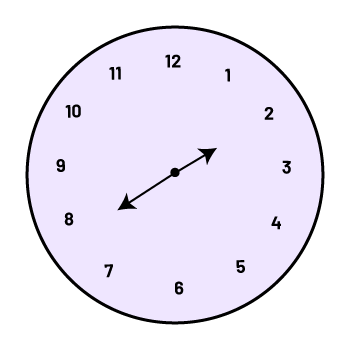
\(30 \ minutes = \frac{1}{2} \ turn = \frac{1}{2} \times 360^{\circ} = 180^{\circ}\)
Once students have developed their understanding of fractions of a rotation using concrete materials, they are able to represent them on circles drawn on paper.
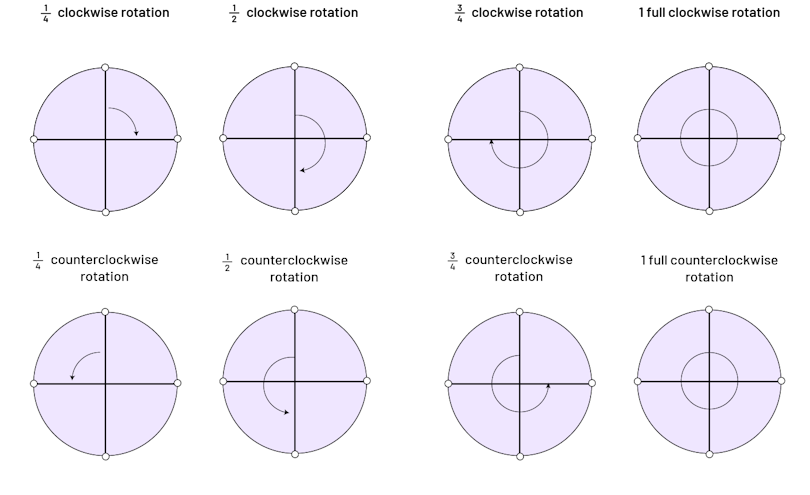 image A series of circles circle whose horizontal axis and vertical axis have been drawn, showing the rotation clockwise, a quarter of all, a half turn, three quarters of all and a whole.A series of circles circle whose horizontal axis and vertical axis have been drawn, showing counterclockwise rotation, clockwise, quarter turn, half turn, three quarter turn and one full turn.
image A series of circles circle whose horizontal axis and vertical axis have been drawn, showing the rotation clockwise, a quarter of all, a half turn, three quarters of all and a whole.A series of circles circle whose horizontal axis and vertical axis have been drawn, showing counterclockwise rotation, clockwise, quarter turn, half turn, three quarter turn and one full turn.
Students should experience rotating shapes using one of the vertices of a shape as the centre of rotation. The use of various tools (for example, tracing paper, polar coordinate paper, square, dynamic geometry software) to perform the rotation according to the specified fraction of a turn helps the students to better understand this transformation. The students also perform rotations whose centre is located on the outline of the shape, inside the shape and outside the shape.
Example
Rotation of a quarter turn clockwise, with the centre of rotation:
- on a vertex of the shape;

- on the outline of the shape or inside the shape;
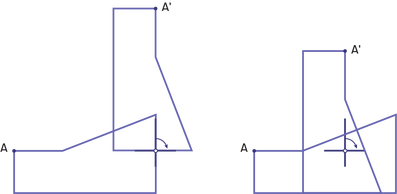
- outside the shape.
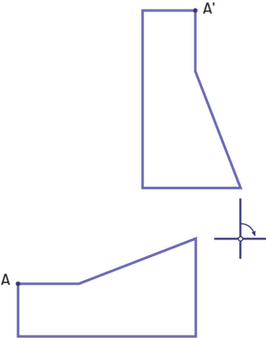
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 32-35.
Example
Rotation about the Origin in a Cartesian Plane at a Given Angle
Rotate triangle ABC 90° and 180° clockwise. Describe the effect of these rotations on the coordinates of the image.
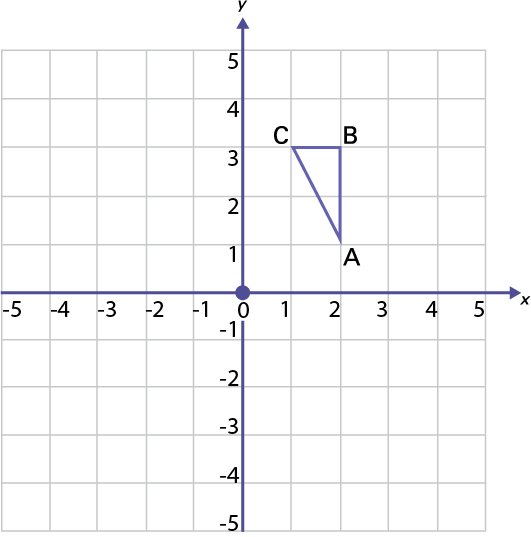 image A triangle « A » « B « C » is placed on a Cartesian plane at the following coordinates. « A » (opening parenthesis) 2, one (closing parenthesis), « B » (opening parenthesis) 2, 3 (closing parenthesis), « C » (opening parenthesis) one, 3 (closing parenthesis)
image A triangle « A » « B « C » is placed on a Cartesian plane at the following coordinates. « A » (opening parenthesis) 2, one (closing parenthesis), « B » (opening parenthesis) 2, 3 (closing parenthesis), « C » (opening parenthesis) one, 3 (closing parenthesis)
I now rotate triangle ABC by 90° (a quarter turn).
In the coordinates of the points, the value of y and the value of the x are interchanged and the value of y becomes the opposite (changes sign).
Original shape → image
(x, y) →(y, -x)
A (2, 1) → A' (1, -2)
B (2, 3) → B' (3, -2)
C (1, 3) → C' (3, -1)
I notice that the rotation “turns” the original shape counterclockwise around the point (0,0) 90 degrees. I also observe that even if the shape A'B'C' no longer has the same coordinates, the rotation has reproduced a figure congruent with the original shape.
I now rotate triangle ABC by 180° (half a turn). In the coordinates of the points, the value of x and the value of y are the opposite (change sign).
Original shape → image
(x, y) →(-x, -y)
A (2, 1) → A' (-2, -1)
B (2, 3) → B' (-2, -3)
C (1, 3) → C' (-1, -3)
I notice that when the rotation “turns” the original shape counterclockwise around the point (0,0) at 180 degrees the figure is upside down. I also observe that even if the shape A'B'C' no longer has the same coordinates, the rotation has reproduced a figure congruent with the original shape.
Source: translated from En avant les maths!, 7e année, CM, Sens de l’espace, p. 14-16.
Skill: Predicting the Results of Translations, Reflections and Rotations in a Cartesian Plane
In order to be able to predict the results of transformations, the student must understand the effect of the transformations on the coordinates of each of the points of the shape. Thus, its predictions will be based on a real understanding of the concept of transformations.
When translations, reflections and rotations are carried out on a shape, it keeps its dimensions (lengths and angles) and is only placed differently in space.
Unlike dilations, translations, reflections and rotations produce congruent images.
In the junior years, students predict the result of a transformation and describe what will happen to the object as the transformation is performed. As a result of guided investigations, students will eventually be able to look at the original orientation of an object and the result of a transformation and describe what transformation was performed without seeing the transformation occur.
In addition, at the start, the student tackles the different transformations individually. The more the student understands their properties, the more they should be able to see that there are connections between them. A flexible pedagogical approach with questioning that allows the student to reflect and establish links between the different types of transformations is preferred.
Here are some sample questions to guide the student in developing spatial reasoning:
- What do you notice about the image of the transformation?
- Are there other transformations that would allow you to obtain the same image?
- Which one do you think is the most effective? Why or why not?
- Compare the translation with the other transformations you have learned. What do you notice?
- What transformations could have the same image?
Source: adapted from A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 34.
Knowledge: Translation, Reflection, Rotation, Cartesian Plane (Prior Knowledge)
Translation. A transformation that moves every point on a shape the same distance, in the same direction, to form a congruent shape. A translation image is the result of a translation.
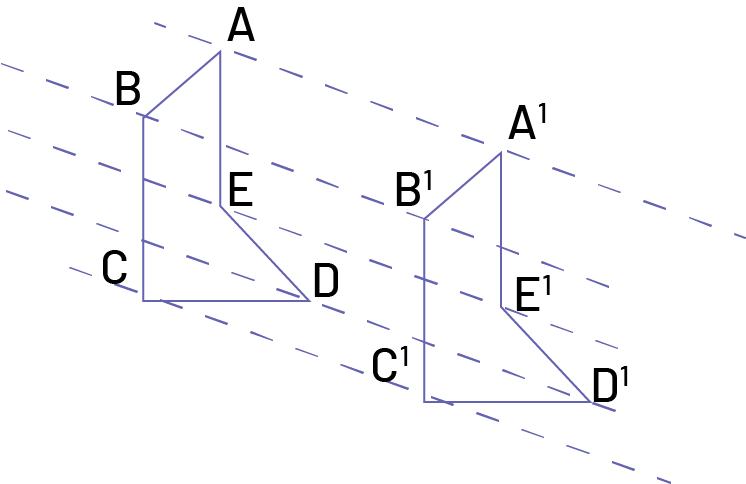
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
A translation is defined by its distance and direction. It may be represented symbolically by use of a translation vector (with or without an arrow). It represents a linear and horizontal, vertical or oblique movement in which the original shape and the image are congruent. The distance between each point on the initial shape and the corresponding point on the image is constant. The orientation of the image will be the same as the orientation of the initial shape.
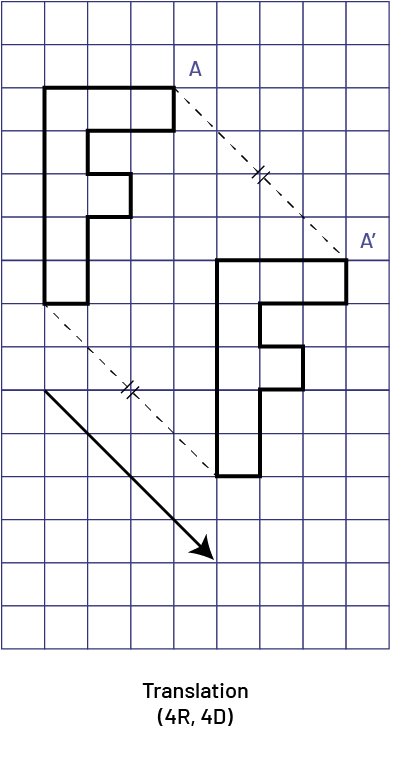 image A capital « F » shaped figure is translated 4 units down and 4 units right.A segment which starts from a vertex of the initial figure and is parallel to the same point on the translation figure.Translation (opening parenthesis) 4 « D », 4 « B » (closing parenthesis).
image A capital « F » shaped figure is translated 4 units down and 4 units right.A segment which starts from a vertex of the initial figure and is parallel to the same point on the translation figure.Translation (opening parenthesis) 4 « D », 4 « B » (closing parenthesis).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 36-37.
Vector. A quantity that has both direction and distance (magnitude). For example, a translation vector could be “right 4, down 3”, or described on the Cartesian plane as (x + 4,y – 3).
Reflection. A transformation that flips a shape over a line to form a congruent shape. A reflection image is the mirror image that results from a reflection.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
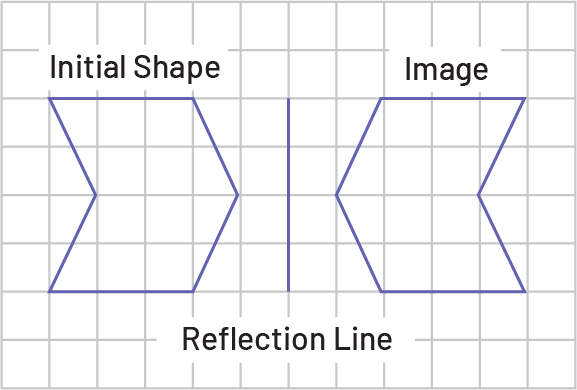
A reflection is a reflexive movement perpendicular to a reflection line. Each point on the original shape and the corresponding point on the image are at the same distance from the reflection line. The original shape and the image are congruent, but the orientation of the image is different from the orientation of the original shape.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Géométrie et sens de l'espace, Fascicule 2, p. 36.
Rotation. A transformation that turns a shape about a fixed point to form a congruent shape. A rotation image is the result of a rotation.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
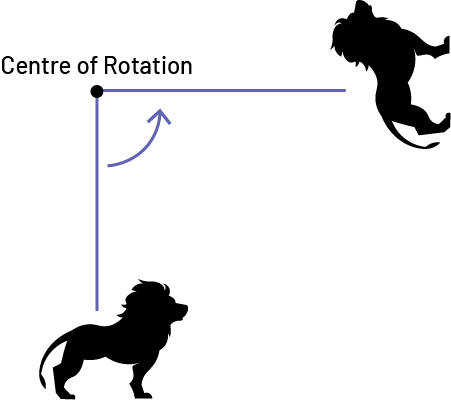
A rotation is a transformation that moves every point of a shape around a fixed point, often called the origin or point of rotation. A rotation creates an image that is congruent to, and also preserves the orientation of, the original shape.

The point of rotation can be found anywhere on the plane, either outside the shape or within it.

When the point of rotation is found at a vertex of the shape, the original shape and its image will share the point.
Source: A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 36.
Cartesian plane. A plane that is subdivided into four quadrants by a horizontal axis (x-axis) and a vertical axis (y-axis) intersecting at a point called the origin. A point (x, y) is used to describe the location on the Cartesian plane relative to the origin (0, 0).

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
