E2.1 Describe the differences and similarities between volume and capacity, and apply the relationship between millilitres (mL) and cubic centimetres (cm3) to solve problems.
Skill: Describing the Difference and Similarity between Volume and Capacity
Volume and capacity describe three-dimensional measurements. Volume is the measurement of space occupied by an object. If the object is placed in a container filled with water and the water it displaces is collected, the number of mL (or cm3) collected corresponds to the volume of the object. For geometric figures that are not very complex, it is possible to calculate this volume with mathematical formulas.
The capacity is the maximum amount that a container can hold. So, when we talk about volume and capacity of a container, we are talking respectively about the volume of the container and that of the contents. Both are therefore measured in mL or cm3.
For smaller or larger volumes, students will see different metric units in Grade 8.
Source: adapted from The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Skill: Solving Problems Using the Relationship between Millilitres (mL) and Cubic Centimetres (cm3)
In Grade 7, students must recognize that a volume of 1 cm3 has a capacity of 1 mL, that is 1 cubic centimetre = 1 millilitre. This relationship means that each millilitre of water in any container occupies a space of 1 cm3. Thus, if we pour 20 mL of water into a container, the water will occupy a space of 20 cm3.
Larger units of volume and capacity also have relationships. For example, a volume of 1 dm3 is equivalent to a capacity of 1000 mL or 1 L.
To help students understand this relationship, teachers can use two activities: one based on the concept of the capacity of a container, the other based on the concept of the volume of a three-dimensional object. These two activities are briefly described in the examples below. In each case, it is important to let students explore the relationship between these two metric units through experimentation, by coming up with a conjecture, and verifying it.
Example 1 (Capacity of a Container)
Provide students with a container whose capacity can be easily determined (for example, a plastic container in the shape of a rectangle-based prism) and a test tube graduated in millilitres. Ask students to determine the internal volume (capacity) of the container using centimetre cubes and express it in cm3. Then ask them to fill the container with water and pour it into the test tube to determine its capacity. In the mathematical discussion, point out that the measurement of the container's capacity in cm3 is very similar to the measurement of the volume of water in mL in the test tube. Point out that the small differences in these measurements may be due to the difficulty of filling the container to capacity and then pouring it into the tube without losing any.
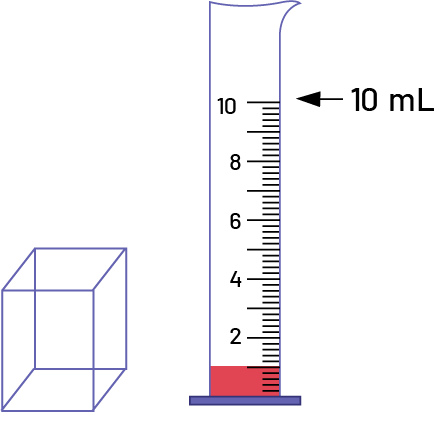
Example 2 (Volume of a Three-Dimensional Object)
Provide students with a three-dimensional object whose volume can be easily determined using centimetre cubes and a test tube graduated in millilitres. Have them first determine the volume of the object (in cm3), then pour some water into the test tube and record the volume of water (in mL). Then ask students to place the object in the test tube and determine the volume of water it displaces. In the mathematical exchange, point out that the measurement, in cm3, of the object's volume is equivalent to the measurement, in mL, of the volume of water displaced. Encourage students to conclude that each millilitre of water (1 mL) occupies a space corresponding to a cubic centimetre (1 cm3).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 67-68.
Mathematical Formulas for Calculating the Volume of Various Three-Dimensional Objects
Note: In the formula for measuring volume, \(V = A_{base} \times H\), the variable upper case H represents the height of the prism. The variable lowercase h, on the other hand, represents the height of the polygon that forms the base of the prism.
Example:
Cube or Right Square-Based Prism (Or Rectangle-Based)
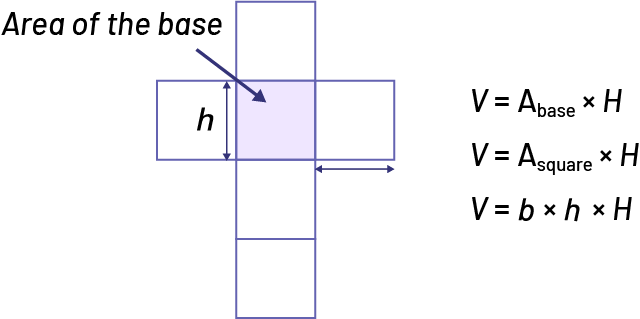image Development of a cube.The square in the middle is the area of the base. The size of one of its sides is the height « h ».« V » equals « A » index base, multiplied by « H ».« V » equals « A » squared, multiplied by « H ».« V » equals « B » multiplied by, « h » multiplied by, « H »
Right Triangle-Based Prism
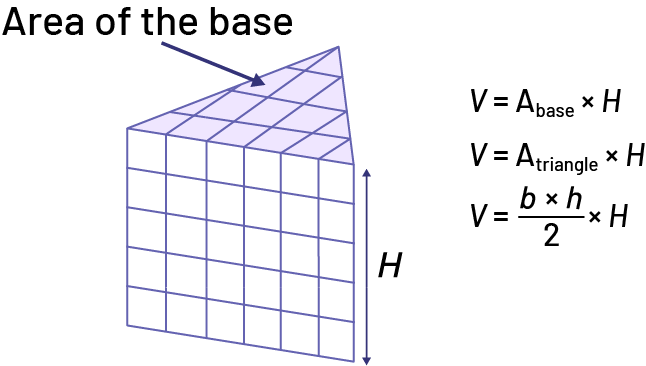image Right prism with triangular base. One of the triangles is the area of the base. One of the sides of the square is the height « H ».« V » equals « A » index base multiplied by, « H ».« V » equals « A » subscript triangle multiplied by, « H ».« V » equals « b » multiplied by « h » divided by 2, multiplied by, « H ».
Right Parallelogram-Based Prism or Oblique Rectangular-Based Prism
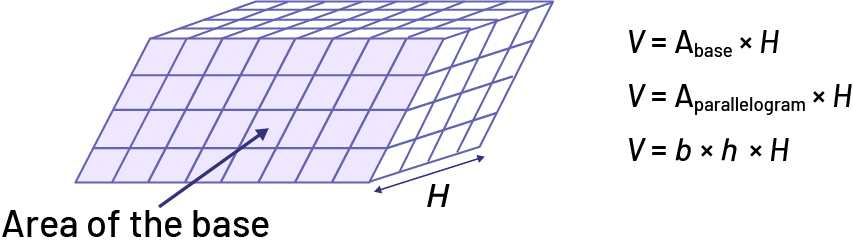image Right prism whose base is a parallelogram or oblique prism with a rectangular base.« V » equals « A » index base, multiplied by « H ».« V » equals « A » subscript parallelogram, multiplied by « H ».« V » equals « b » multiplied by, « h » multiplied by, « H»
Volume of a cylinder. Measurement of the space occupied by a cylinder.
Note: As with prisms, each layer of a cylinder is identical.
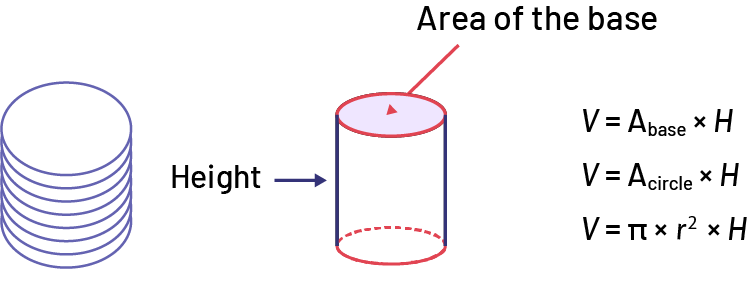image Volume of a cylinder.Cylindrical prism, the base in a circle is the area of the base. The height of the cylinder « H ».« V » equals « A » index disc, multiplied by « H ». « V » equals Pi multiplied by « r » squared multiplied by, « H ».
Source: translated from En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2-3.
Knowledge: Capacity
The capacity is the greatest amount that a container can hold; usually measured in litres or millilitres.
To find the measurement of the capacity of a container, we use the measurement of its interior volume. The capacity measurement is expressed in litres (for example, L, mL, cL, dL).
There are relationships between metric units of volume and capacity: 1 mL of liquid occupies 1 cm3 of space, and a 1 L container has an interior volume of 1000 cm3.
Source: adapted from The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
In the case of a container, it is important to distinguish between its exterior volume and its interior volume (capacity).
Examples
The trunk below has an exterior volume of 1500 cm3 and a capacity (interior volume) of 832 cm3.
The volume of the liquid in the bottle is 275 mL. The capacity of the bottle is 350 mL.
Source: translated from Fiche de la 4e à la 6e année, Attribut volume, p. 2.
Knowledge: Volume
The amount of space occupied by an object; measured in cubic units, such as cubic centimetres.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Volume refers to the size of a three-dimensional space occupied by an object (including any three-dimensional object, liquid or gas), while the capacity of a container refers to the maximum amount of a given substance that it is possible to put inside the container.
Example
I can compare the volume of two containers by checking which takes up more space (for example, by water displacement or by measuring the length, width, and height and calculating the volume).
I can determine the capacity of a thermos by pouring cups of water into it.
Source: adapted and translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 41-42.
Fundamental Concepts
Conservation of Volume
The student who understands this concept realizes that, in most situations, the volume of an object remains the same whether the object is moved, transformed or decomposed.
Example
One bottle contains 250 mL of fruit juice. Lise pours this juice into a glass whose capacity is greater than the capacity of the bottle. What will be the volume of the juice in the glass? (The volume of the juice in the glass remains the same at 250 mL, because moving the juice from one container to another does not change the volume.)
Additivity
The student who understands this concept realizes that the volume of an object is equal to the sum of the volume of each of its parts.
Example
A rectangle-based prism with a volume of 1500 cm3 is made up of a number of pieces of different sizes. Karla found a bag containing four pieces that have a volume of 234 cm3, 416 cm3, 98 cm3 and 585 cm3 respectively. Has she found all pieces to make the prism? (No, because the total volume of the pieces found is equal to 1333 cm3, while the complete prism has a volume of 1500 cm3.)
Structure Associated with the Units of a Right Rectangle-Based Prism
The student who understands this concept realizes that the units of volume are first placed, without space or overlap, to form identical arrays and that these arrays are then juxtaposed in a third dimension to create a right rectangle-based prism.
Example
Conrad wants to determine the volume of the prism illustrated below by considering the different arrays of cubes that could build the prism. How can he do this in three different ways?
He could consider that there are:
- three arrays that are composed of five columns and four rows. The volume of the prism is therefore equal to 3 × [5 × 4] = 60 cubes.
- four arrays that are composed of five columns and three rows. The volume of the prism is therefore equal to 4 × [5 × 3] = 60 cubes.
- five arrays that are composed of three columns and four rows. The volume of the prism is therefore equal to 5 × [3 × 4] = 60 cubes.
Source: translated from Fiche de la 4e à la 6e année, Attribut volume, p. 2.