E2.2 Solve problems involving perimeter, area, and volume that require converting from one metric unit of measurement to another.
Skill: Solving Problems Related to Perimeter, Area and Volume That Require Conversion from One Metric Unit of Measurement to Another
It is important to realize that perimeter, area and volume are respectively one-dimensional, two-dimensional and three-dimensional measurements. This influences the conversion technique slightly.
Examples
In One Dimension
When converting metres to centimetres, we multiply the number of metres by 100, because there are 100 cm in a metre.
For Example:
4 m = 4 (100 cm)
4 m = 400 cm
In Two Dimensions
When converting square metres to square centimetres, the number of square metres is multiplied by 1002 (or 10 000).
For Example:
4 m2 = 4(100)2
4 m2 = 4 × 10 000 cm2
4 m2 = 40 000 cm2
In Three Dimensions
When converting cubic metres to cubic centimetres, the number of cubic metres is multiplied by 1003 (or 1 000 000).
For Example:
4 m3 = 4(100 cm)3
4 m3 = 4 × 1 000 000 cm3
4 m3 = 4 000 000 cm3
The goal is not to memorize these relationships as formulas, but to have the tools to visually represent and understand the relationships, and to use them to calculate unit conversions.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Perimeter, Area, Volume
The perimeter is the length of the boundary of a shape, or the distance around a shape.
For example:
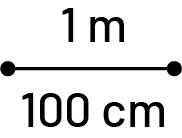
The area is the surface of an object or shape. Since all points are in the same plane, it is a two-dimensional measurement, usually in units of square centimetres and square metres.
For example:
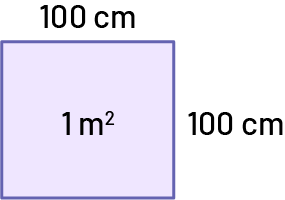
The volume is the amount of space occupied by an object; measured in cubic units, such as cubic centimetres.
For example:
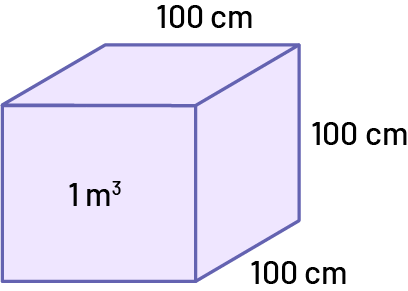
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
