La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

E2.6 Represent cylinders as nets and determine their surface area by adding the areas of their parts.

Skill: Representing Cylinders as Nets

When we represent a cylinder as a net, the lateral surface is in fact a rectangle that is "rolled" to form a circle and whose base is the circumference of this circle.

Area of a Cylinder

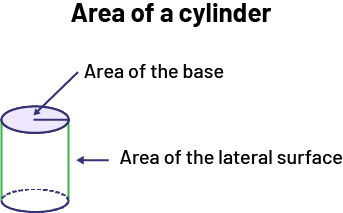
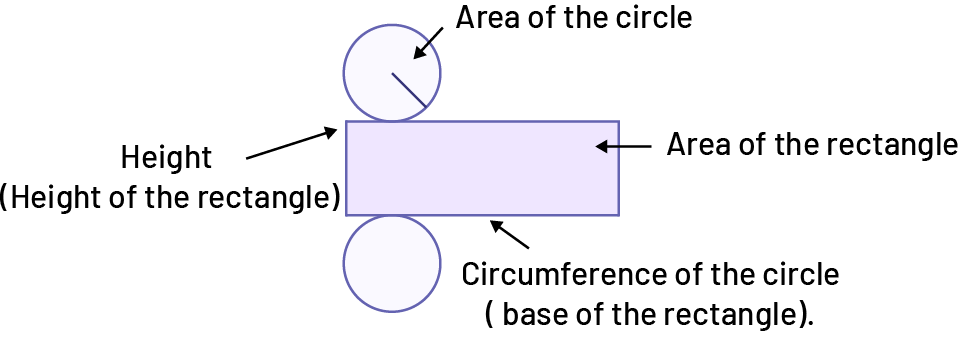
Area of a cylinder.The circular base of a cylinder represents the area of the base.The cylindrical surface of the side to represent is the area of the side surface.Development of a cylinder.The circles represent the area of the disc. The rectangle represents the area of the rectangle. The width side of the rectangle is the height. And the length of the rectangle represents the circumference of the disc.

Source: adapted and translated from En avant, les maths!, 7e année, CM, Sens de l’espace, p. 5.

Skill: Determining the Total Area of Cylinders by Adding the Areas of Their Parts

Area is additive: partial areas can be added together to find a whole area. Finding the surface area of a cylinder is an application of the property of additivity.

Nets help to visualize the two-dimensional shapes that make up a three-dimensional object such as a cylinder. Cylinders, for their bases, have two parallel, congruent faces (see E1.1 for a full list of the properties of cylinders) that are joined by a rectangle (to produce a right cylinder) or a non-rectangular parallelogram (to produce an oblique cylinder).

In real-life contexts, cylinders can have two closed bases (for example, closed tin cans), one closed and one open base (for example, cylindrical pencil holders), or two open bases (for example, pipes; paper towel rolls).

Note: Visualizing the net for a cylinder – imagining it in the “mind’s eye” – involves identifying the shapes that form its faces and recognizing how the dimensions of the cylinder relate to the dimensions of the different faces.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Area of a Cylinder

Area of a cylinder.The circular base of a cylinder represents the area of the base.The cylindrical surface of the side to represent is the area of the side surface.

\(\begin{align} A_{total} &= {\color{green}A_{lateral \ surface}} + 2 \times {\color{purple}A_{base}} \\ &= {\color{green}b \times h} + 2 \times {\color{purple}\pi r^{2}} \\ &= {\color{green}C \times H} + 2 \times {\color{purple}\pi r^{2}} \\ &= {\color{green}\pi d \times H} + 2 \times {\color{purple}\pi r^{2}} \\ &or \\ &= {\color{green}2 \pi r^{2} \times H} + 2 \times {\color{purple}\pi r^{2}} \end{align}\)

Source: translated from En avant, les maths!, 7e année, CM, Sens de l’espace, p. 5.