E2.7 Show that the volume of a prism or cylinder can be determined by multiplying the area of its base by its height, and apply this relationship to find the area of the base, volume, and height of prisms and cylinders when given two of the three measurements.
Skill: Showing That the Volume of a Prism or Cylinder Can Be Determined by Multiplying the Area of the Base by Its Height
Relationship between Area and Volume Attributes
In Grade 7 , teachers should have students discover the relationship between the volume of a right prism, its height and the area of its base. In order for students to establish and understand this relationship, they need to explore various learning situations with manipulatives.
Example
Teachers present students with small right prism boxes like the ones in the picture below and ask them to determine how they might determine the volume.

A student proposes to build a structure that occupies the same space as one of the boxes using 1 cm3 interlocking cubes. The student then counts the cubes used. Since there are 180 cubes, the student concludes that the volume of the box is equal to 180 cm3. The teacher then encourages students to use a strategy other than counting to determine the volume of the structure by asking questions such as:
- This structure looks like a multi-story building. How many floors does this structure have? (It has five floors.)
- What is the area of each floor? How do we know? (The area of each floor is 36 cm2 since it is 6 cm long and 6 cm wide. It is like an array of 6 rows of 1 cm and 6 columns of 1 cm.)
- If the structure had only one floor, what would its volume be? (Its volume would be 36 cm3 since it would be composed of 36 cubes and each cube has a volume of 1 cm3.)
- How then can the volume of the five-story structure be determined? (We have five stories of arrays, each with a volume of 36 cm3, so the volume of the structure is 180 cm3.)
- What relationship do these observations suggest to you? (The volume of a right prism is equal to the product of its base area and its height.)
- How could this relationship be written symbolically? (V = area of the base × h)
This relationship is very important since it allows students to determine the volume of other right prisms (for example, right triangle-based prism). They can also use it to determine the volume of cylinders.
Note that teachers can also provide activities that allow students to explore situations in which there is no relationship between certain attributes. For example, teachers can ask students if there is a relationship between the volume of an object and its mass. To illustrate this, students could be shown a variety of spherical objects (for example, table tennis ball, baseball, basketball, beach ball) and asked to place them, first in order of increasing volume, then in order of increasing mass. Students may conclude that there is no relationship between the volume of an object and its mass.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 79-81.
Volume is measured in cubic units, and the measure represents the number of cubes needed to completely fill an object. Similar to units of area, a cubic unit is an amount of volume, can come in any size, and may look different than a cube (for example, a cubic metre of sans could be in a pile). Units of volume can be decomposed, rearranged, partitioned, and redistributed to better fill a volume and minimize gaps and overlaps
Indirectly measuring the volume of shapes is often quicker and more accurate than measuring volume directly (namely, by laying out and stacking cubes).
All prisms and cylinders have two congruent bases that are parallel to each other (see E1.1). This means that, at any height in a prism or cylinder, a “slice” could be made, if the slice is parallel to the base – the cross-section that is created will have congruent faces. From top to bottom, the area of any slice, or layer, is consistent, and it is always equal to the area of the base. This geometric property of prisms and cylinders forms the basis for the formula for calculating their volume. Right prisms and right cylinders have bases that are perpendicular to their sides.
The row-and-column structure of an array, which helps structure the count of square units for area (see Grade 4, E2.5), also helps structure the count of cubic units and is used to indirectly measure volume.
- A unit is repeated to produce the given length (a row).
- A row is repeated to produce the given area of the base (a layer).
- A layer is repeated to produce the given height (the volume).
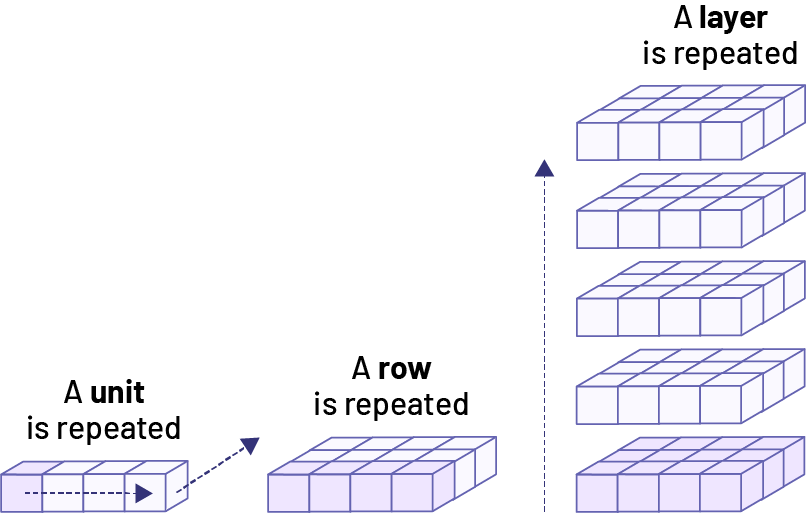
The area of the base determines how many cubes can be placed on the base, which forms a single unit – a layer of cubes. The height of the prism determines how many layers of cubes it takes to fill the volume. Therefore, the formula for finding the volume of a rectangular prism is area = base × height.
The same is true for any prism or cylinder: the area of the base determines how many cubes can be placed on its base, and the height determines how many layers of cubes it takes to fill the volume. This means that the formula for finding the volume of any cylinder or prism is area of the base × height.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
The relationship between the base and height of shapes or three-dimensional objects underlies all formulas for determining the area or volume of shapes and three-dimensional objects and are based on this organized way of counting the number of square units or cubic units.
image A rectangle.Area equals base multiplied by height.A parallelogram.Area equals base multiplied by height.Triangle.Area equals base multiplied by height, divided by 2.Trapeze.Mean equal area of the bases multiplied by height.« A » equals (opening parenthesis) « b » plus « B » (closing parenthesis) multiplied by « h », divided by 2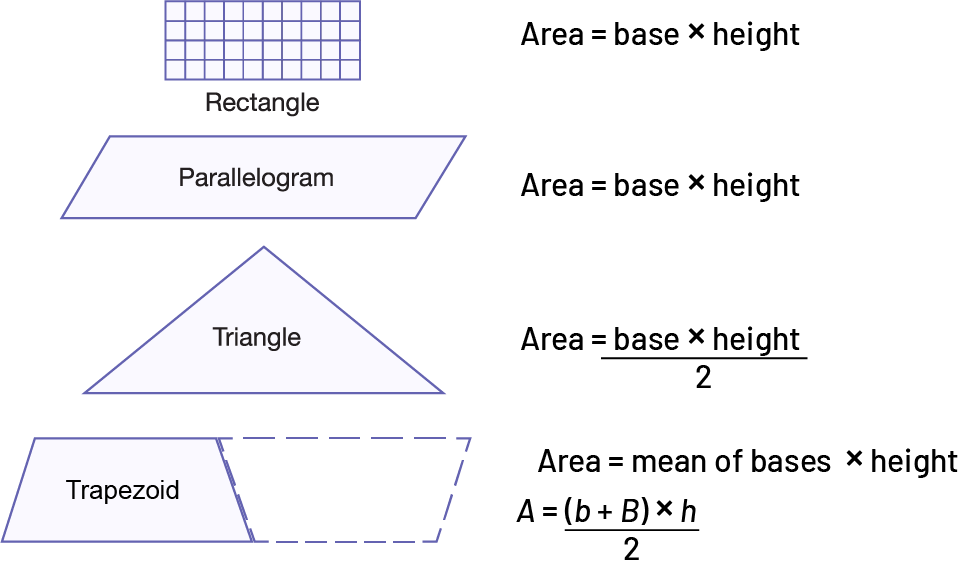


Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, Mesure et géométrie, Fascicule 3, p. 52-53.
Skill: Calculating the Base Area, Volume and Height of Prisms and Cylinders When Two of the Three Measurements Are Known
Apply a Formula
A measurement formula is an equation that represents a fundamental relationship between the measurement of different attributes of an object. It makes it possible to determine the measurement of an unknown attribute when the measurement of the other attributes is known (for example, determining the measurement of the volume of a right prism from when its height and area of base are known).
It is important that students are given many opportunities to explore the relationships among measurable attributes of an object before they construct and apply a formula. According to Van de Walle and Lovin (2008b, p. 284), “a conceptual approach to formula development helps students understand that these tools are useful and effective ways to measure various attributes of the objects around us. Once they construct formulas in a meaningful way, […] they will know how to infer formulas from what they already know.”
Once students understand the meaning of the formulas, they must learn to use them correctly. Teachers should present students with a variety of situations that require them to use a formula to determine the measurement of some attribute. Teachers should use this opportunity to make connections to the Algebra strand.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 99-100.
