E1.3 Perform dilations and describe the similarity between the image and the original shape.
Activity 1: Perfoming Dilations
a) Perform a dilation of scale factor 2 to the triangle below and describe the similarity between the image and the original shape.
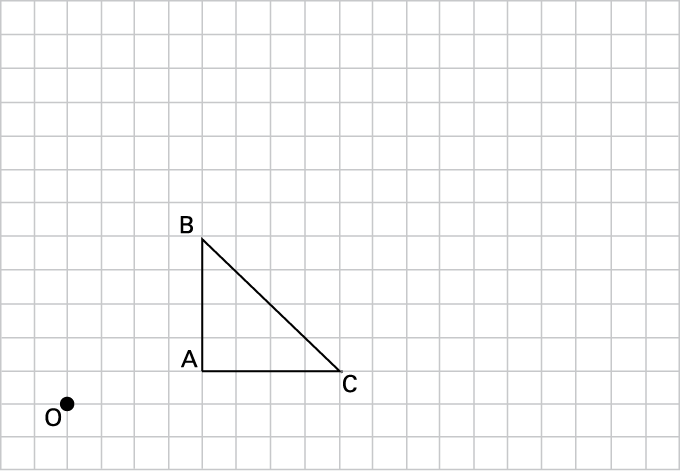
b) On a sheet of grid paper, draw a triangle whose sides measure 3 cm, 4 cm and 5 cm respectively. Locate a point O outside your triangle. Draw a line starting from point O to each of the vertices of triangle ABC as shown below.
Apply a dilation of scale factor \(\frac{1}{2}\) to your original shape. How are your triangles the same? How are they different? What conclusions can you draw?
Possible Answers
a) For each vertex ABC, I draw a line connecting each point to the dilation point. Using a ruler, I measure the distance between each vertex of the shape and the dilation point. I then multiply each of the distances by the scale factor 2. For example, I measure the length of line OA. Line OA is 4 cm long. I then draw a line OA' of 8 cm passing through point A, because the dilation ratio is 2. I repeat the same procedure to form lines OB' and OC'.
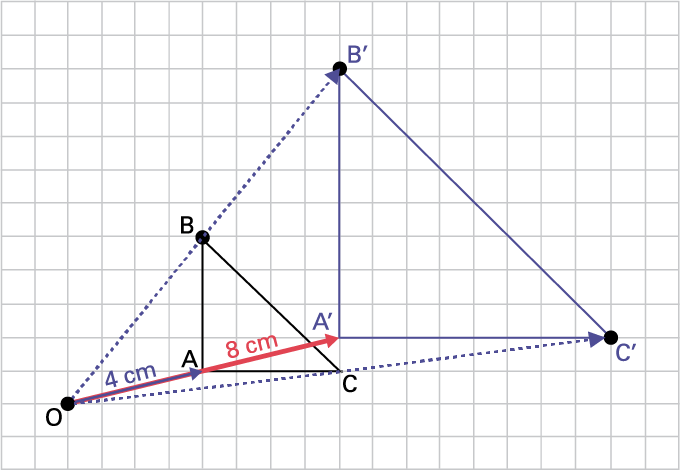image On a square grid, a triangle « A » « B » « C » is drawn. A little out of step is drawn the triangle "« A » prime, « B » prime, « C » prime.A point « O » is placed in such a way as to be able to line up the points « O » « A » « A » prime, on a line, but also « o » « b » « B » prime and, « O » « C » « C » prime.
This dilation represents a transformation that enlarges the original by the given scale factor. I notice that the sides of triangle A'B'C' are twice as long as those of triangle ABC. Moreover, the distance between the dilation point (point O) and the vertices of the image is twice as great as the distance between the dilation point and the vertices of the original shape. The figures have the same shape, but they are different sizes. The two figures are proportional. Their angles remain the same, and the length of their sides is enlarged according to the dilation factor.
b) For each vertex ABC, I draw a line that connects each point to the dilation point. Using a ruler, I measure the distance from each vertex in the shape to the dilation point. I then multiply each of the distances by the scale factor (\frac{1}{2}\). For example, I measure the length of the line between O and A. The line OA measures 5 cm. I then draw a point on the line at 2.5 cm to form the line OA'. I repeat the same procedure to form the lines OB' and OC'.
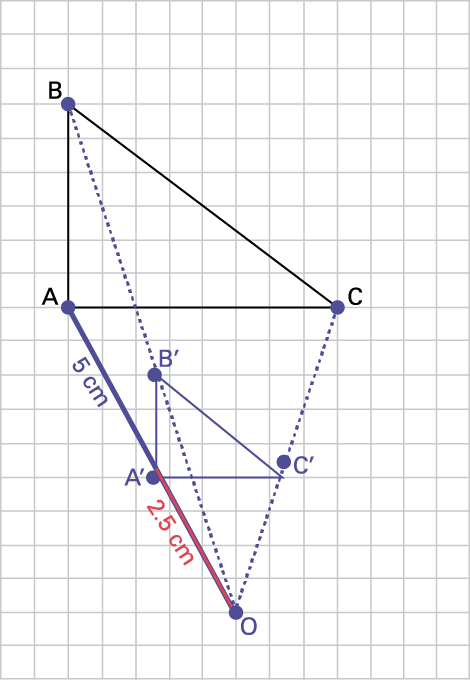image On a square grid, a triangle « A » « B » « C » is drawn. A little out of step is drawn the triangle "« A » prime, « B » prime, « C » prime.A point « O » is placed in such a way as to be able to line up the points « O » « A » « A » prime, on a line, but also « o » « b » « B » prime and, « O » « C » « C » prime.
This dilation represents a transformation that reduces the original shape by the given scale factor, \frac{1}{2}\. I notice that the sides of triangle A'B'C' are half of the lengths of the sides for triangle ABC. Also, the distance between the dilation point and the vertices of the image is half the distance between the dilation point and the vertices of the original shape. The figures have the same shape, but are different sizes. The two figures are proportional. Their angles remain the same, and the length of their sides is reduced according to the dialation factor.
Source: translated from En avant les maths!, 7e année, CM, Sens de l’espace, p. 5-7.
Activity 2: Describing Dilations
a) Find the scale factor used for the dilation of the triangle, taking into account the dilation point.
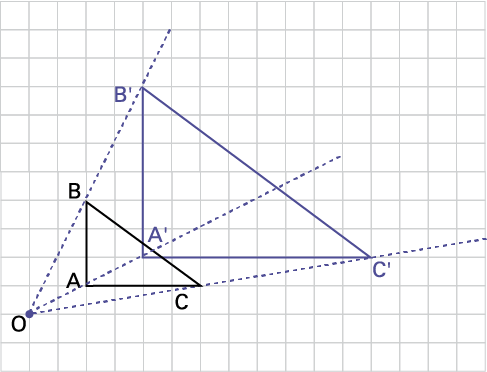image On a square grid, a triangle « A » « B » « C » is drawn. A little out of step is drawn the triangle "« A » prime, « B » prime, « C » prime.A point « O » is placed in such a way as to be able to line up the points « O » « A » « A » prime, on a line, but also « o » « b » « B » prime and, « O » « C » « C » prime.
b) Look at these two shapes. What do you notice?
image Figure « A « « B » « C « « D » is reproduced enlarged, it is doubled. They become« A » prime, « B » prime, « C » prime, « D » prime. This is called homothety.
Source: translated from En avant les maths!, 7e année, ML, Sens de l’espace, p. 17.