E2.1 Describe the differences and similarities between volume and capacity, and apply the relationship between millilitres (mL) and cubic centimetres (cm3) to solve problems.
Activity 1: Exploratory Activity on Objects That Can Be Used as Units for Volume
Goal
In this activity, students discover several objects that can be used as benchmarks for volume.
Materials
- cereal boxes
- shoe boxes
- gift boxes of various sizes
- interlocking cubes
- cylindrical containers such as circular chip boxes, paper towel rolls.
Instructions
Provide students with several common objects (for example, cereal boxes, shoe boxes, gift boxes of various sizes, interlocking cubes, cylindrical containers).
Ask students how they might measure the volume of these objects.
Have students estimate and then determine the volume of each object by re-constructing it, using the smaller objects.
Note: Encourage students to use various 3-D shapes as units of measurement for volume. They will realize that using cubes provides a better estimate of the space occupied by a three-dimensional object.
Examples
- To construct a three-dimensional object that occupies approximately the same space as a large box, 80 cereal boxes were used.
- To construct a three-dimensional object that occupies approximately the same space as a container of tennis balls, three rolls of paper towels were used.
- To construct a three-dimensional object that occupies the same space as a box of tissues, 264 interlocking cubes were used.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2: Exploratory Activity on Objects That Can Be Used to Build Structures of a Given Volume
Goal
In this activity, students construct three-dimensional objects with a given volume.
Materials
Interlocking cubes
Instructions
Ask students to construct a cubic decimetre using base ten materials.
Invite students to estimate the volume of large objects using their constructed cubic decimeter.
Examples of Large Objects
- A recycling bin (approximately 60 dm3)
- A school bag (about 24 dm3)
Students should be able to explain the process used to obtain their estimation. Questions to guide them include:
- How did you arrive at your estimation?
- What strategies did you use? Ask the students to construct three-dimensional objects with volumes expressed in dm3.
Ask students to construct three-dimensional objects with volumes expressed in dm3.
Examples of Objects
- A three-dimensional object having a volume of 10 dm3.
- A three-dimensional object having a volume of 7 dm3.
Ask students to exchange their objects with a peer and to check each other's construction to determine if the requested volume has been achieved.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 3: Capacity Measurement Activities with Standard Units - One Cubic Decimetre
Goal
In this activity students build a cubic decimetre to develop a sense of what a litre represents.
Materials
- grid paper (see Appendix 1)
- scissors, tape
- rigid cardboard
- one litre container (one per team)
- dry fill material (rice, sand, corn kernels, etc.)
Instructions
Ask students to cut out five cardboard squares with each side measuring 1 dm (use cm2 grids if necessary).
Ask them to glue the squares together to form a cubic decimetre. It is not necessary to have the top face.
Impress on them that the interior measurements of the cube must be 1 dm.
Ask students to fill the cubic decimetre with the fill material and to compare this content with the content that the one-litre container can hold.
Ask the question: “What is the relationship between the capacity of a 1 dm3 container and the capacity of a litre container?”.
Note: Model appropriate expressions, such as 1 dm3 is equivalent to 1 L or a 1 dm3 container has the same capacity as a 1 L container.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 4: Relationship Between Units for Capacity, Mass, and Volume
Goal
In this activity students determine the relationship between the units of capacity, mass and volume if the object is pure water at 4°C under normal pressure. For example, 1 litre of pure water has a mass of 1 kg and occupies the same space as 1 dm3.
|
Capacity |
Mass |
Volume |
|
1 mL |
1 g |
1 cm3 |
|
1 L |
1 kg |
1 dm3 |
|
1 kL |
1 t |
1 m3 |
Materials
- one litre container
- one cubic decimetre
- a pan balance and masses of 1 g, 1 mg and 1 kg
- pure (distilled) water at 4°C (tap water at room temperature is acceptable for this activity)
- rice, beans or sand
Instructions
Invite students to check, using rice, beans, or sand, whether the contents of the one litre container occupy the same space as the cubic decimetre.
Ask students to justify their answer.
Answer: Yes. When I fill the one litre container with rice and pour those contents into the cubic decimetre, it is the same amount.
Ask students to explain the relationship between the capacity of a one litre container and the volume of a cube with each edge measuring 1 dm.
Response: It's the same thing. The contents of the one litre container fits exactly in the cubic decimetre.
Have students use the pan balance to determine the mass of one litre of water and explain their strategy.
Answer: I determine the mass of the empty one litre container using the masses. I then filled the container with water and determine its mass again. The total mass I added is equivalent to the mass of one litre of water.
Then ask them the following questions.
Note: For this activity, students should be allowed some margin of error because of the objects used.
- What is the mass, in kg, of one litre of water?
Answer: The mass of one litre of water is 1 kg.
- How much water is contained in 1 dm3?
Answer: The amount of water contained in 1 dm3 is 1 litre.
- What is the mass of the quantity of water contained in 1 dm3?
Answer: The mass of the amount of water contained in 1 dm3 is 1 kg.
- What is the relationship between the mass, in kg, of a litre of water, the capacity of the container and the space occupied by that amount of water? How do you know this?
Answer: all three measurements are equivalent. 1 L = 1 kg = 1 dm3.
- What is the relationship between the units of capacity, mass and volume if we have 1 g of water? 1 kL of water?
Answer: A millilitre of water has a mass of 1 g and a volume of 1 cm.3. One kilolitre of water has a mass of 1 ton and a volume of 1m3.
- Would the relationship between mL, cm3 and g be the same with a liquid other than water (oil, liquid soap, etc.)?
Answer: Most of the time, no. Many liquids do not have the same density as water. The mass of 1 L of liquid soap will be greater than 1 kg.
Caution: The student can experiment with other liquids and conclude that the relationship between 1 mL, 1 cm3 and 1 g does not exist with liquid soap or oil. However, it should not be expected that they will understand the reasons at this age.
- Does this ratio remain the same if you use rice? beans? sand? How do you know?
Answer: No, because these products are heavier than water. The mass of 1 L of rice will be greater than 1 kg.
Caution: The student can experiment with rice or sand and reach the conclusion that there is no connection between 1 mL, 1 cm3 and 1 g.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 5: Volume Measurement Activities with Standard Units - The Cubic Metre
Summary
In this activity students build the framework of a cube with each side measuring 1 m.
Materials
- two large flip chart sheets per team of three
- metres
- adhesive tape
Instructions
Make rolls that are a metre or more in length. If you fold the sheet of paper tightly enough from one corner, the roll formed is stiffer than if you just roll the sheet into a tube.
Note: 12 sheets are needed for each cube.

Ensure that each roll is at least 1 m long. Fold the ends if necessary.
Tape the rolls together to form a cube with edges 1 m long. The cube formed has a volume of 1 m3.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 6: Volume Measurement Activities with Standard Units - Base Ten Small Cubes
Goal
In this activity students determine the volume of various objects using base ten small cubes.
Materials
- small boxes of various sizes
- interlocking cubes
- base ten small cubes (in large quantities)
- cylindrical containers
Instructions
Provide students with several common objects (for example, small boxes of various sizes, interlocking cubes, base ten small cubes, cylindrical containers).
Invite students to estimate the volume of each object if the unit is the cubic centimetre (the small cube).
Have students determine the volume of each object by constructing a three-dimensional object that occupies approximately the same space using base ten small cubes. For example, to construct an object that occupies approximately the same space as a deck of playing cards, 126 small cubes were used.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 7: Measurement Activity for Home - What Space Does This Object Occupy?
Materials
- 14 small cubes (base ten material)
- 2 cm × 2 cm × 2 cm interlocking cubes
Instructions
Parent
Give your child six small cubes (1 cm × 1 cm × 1 cm) and ask them to build a tower six cubes high.
Ask your child the volume of this tower (the space that this tower occupies).
Answer: The tower has a volume of 6 cubic centimetres or 6 cm3.
Ask your child to estimate whether the interlocking cube structure (2 cm × 2 cm × 2 cm) occupies a larger or smaller space than the tower they built (without specifying that the cube measures 2 cm × 2 cm × 2 cm).
Let the child calculate and draw their own conclusions.
Caution! Your child should recognize that the volume of a longer prism can be smaller than that of a cube with shorter edges.
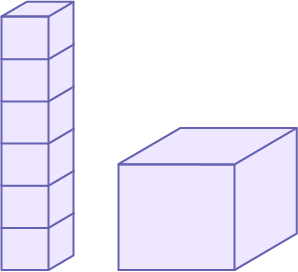
The volume of the tower of six small cubes is 6 × 1 cm3 or 6 cm3.
The volume of the large cube is 2 × (2 × 2 × 1 cm3) or 8 cm3.
The edges of the large cube are shorter than the length of the tower.
So, how can the shorter prism have a larger volume?
Your Child:
- builds the 6 cm3 tower and determines its volume.
- estimates whether an interlocking cube (2 cm × 2 cm × 2 cm) has a larger or smaller volume than the tower.
- builds a 2 cm × 2 cm × 2 cm cube to verify the estimation.
- draws a conclusion and justifies the answer.
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Consideration for Volume Activities with Blocks
Volume: The student can represent a cubic centimetre with the small cube from the base ten material. It is best not to use the interlocking cubes, since some of these cubes are 2 cm long, so their volume is 8 cm3 rather than 1 cm3. When the student understands that 1 cm3 is equivalent to 1 mL, it helps them to visualize this quantity better by associating it with the capacity of a bottle of water. The cubic metre is more difficult to estimate. The student can represent a cubic metre by associating it with the volume of an appliance, such as a clothes washer.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, Mesure et géométrie, Fascicule 3, p. 45.
Activity 8: Activity on the Volume Attribute - What Is a Volume?
Goal
In this activity, students distinguish between the volume of a container and its capacity.
Materials
- transparent containers of various sizes and capacities
- water
- thermos
- measuring cups of various capacities
Instructions
Have students determine the capacity of a thermos using a measuring cup.
Note: It is important that the container chosen has a thick enough sidewall for the activity to be effective and not confusing to the student.
In a larger container filled to the brim with water, submerge the thermos and collect the overflowing water. Or in a larger container of water with a line drawn across it, submerge the thermos/mug and draw a second line across the water level.
Measure the amount of water that has overflowed or shifted using a measuring cup.
Compare the amount of water that has overflowed or shifted (for example, the volume of the thermos jug) with the capacity of the thermos.
Point out to students the difference between the volume of the thermos glass (the amount of water that spilled or moved) and the capacity of the thermos (the amount of water it can hold).
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 9: Capacity or Volume
Form teams of two, then give them a closed thermos and a measuring cup large enough to immerse the thermos in. Have them determine the volume and capacity of the thermos and use the results to explain the difference between these two attributes.
When all teams are finished, bring students back together and discuss the strategies used and the results. Point out that the volume of the thermos is larger than the capacity because it is the outside volume of the thermos (space it takes up), while the capacity is the inside volume (the amount that it holds).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 168.
Activity 10: Empty or Full? With or Without a Cap?
First, show students two identical, closed bottles, one empty and one full.
Ask them the following question: “In your opinion, if you immerse these two bottles in a container of water, which one will displace the greatest volume of water? Why?”.
Note: Some students may believe that the full bottle will move a greater volume of water than the empty bottle because it has a greater mass.
Form teams of two, provide them with the necessary materials (for example, empty bottle, full bottle, measuring cup, water) and ask them to check their answers using the strategy of their choice.
When all teams have finished, bring the students back together and discuss the strategies used and the results obtained. Encourage students to conclude that the volume of water displaced by the two bottles is the same because they occupy the same space. They therefore have the same volume.
Second, show students two identical empty bottles, one with a cap and one without, and then ask them the following question: “If you immerse these two bottles in a container of water, which one do you think will displace the most water? Why?”.
Note: Some students may think that both bottles will move the same amount of water because they are both empty.
Form teams of two, provide them with the necessary materials (for example, bottle with cap, bottle without cap, measuring cup, water) and ask them to check their answers using the strategy of their choice.
When all teams have finished, bring students together and discuss the strategies used and the results obtained. Encourage students to conclude that the bottle with a cap moves a greater volume of water than the bottle without a cap because it takes up more space.
In fact, the volume of water displaced by the bottle with a cap corresponds to the space occupied by its sidewalls and by the air inside the bottle, whereas the volume of water displaced by the bottle without a cap corresponds to the space occupied by its sidewalls only.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Mesure, p. 169.
