E2.7 Show that the volume of a prism or cylinder can be determined by multiplying the area of its base by its height, and apply this relationship to find the area of the base, volume, and height of prisms and cylinders when given two of the three measurements.
Activity 1: Volume of a Right Rectangle-Based Prism
Goal
This activity allows the student to realize that the volume of a prism is determined by constructing a three-dimensional object that occupies the same space as the prism.
Materials
- various rectangle-based prisms (shoe box, cereal box, etc.).
- many interlocking cubes of 1 cm by 1 cm.
Form teams of two.
Give each team a prism and a fair amount of interlocking cubes.
Ask students to reproduce the prism with their cubes.
Ask the following questions:
- What unit of measurement did you use to reproduce the prism?
- How many cubic centimetres did it take to reproduce the length of the prism?
- How many cubic centimetres did it take to reproduce the width?
- How many cubic centimetres did it take to reproduce the height?
- What are the dimensions of your prism?
- What is its volume in cubic centimetres?
- What is the relationship between the dimensions of your prism and its volume?
- How can we determine the volume of any prism?
Example of an answer from a team that has a prism of 5 cm by 4 cm by 3 cm: On the length, we can place five 1 cm3 units. On the width, we can place four 1 cm3 units. Thus, we have a base whose area measures 5 × 4 units. On the height, we can place three 1 cm3 units. Therefore, the volume of the box is 5 × 4 × 3 units (cm3), or 60 cm3.
Note: Have students realize that determining the volume of a prism is determining the area of its base (5 × 4 units) and multiplying it by its height (3 units). Thus, the volume of a prism can be expressed as follows:
\(V = area \ of \ the \ base \times height \)
Source: L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 2 : Volume of a Right Triangle-Based Prism
Goal
Through this activity, students will be able to determine the volume of a right triangle-based prism using the formula for calculating the volume of a right prism.
Materials
- one rule per team
- a square or a goniometer per team
- triangle-based prisms
- blank paper, pencil and eraser.
Note: Coding software could be used to calculate the prism's volume from the formula.
Directions
Form teams of two.
Give the teams a triangle-based prism.
Ask students to identify the bases of the prism.
Ask them to draw the outline of the prism's base on a piece of paper.
Using a square, they trace the height of the triangle and measure it in centimetres (2 cm).
Ask the questions below.
Here is an example with a prism.
- What is the length of the triangle's base?
- Expected answer: The length of the triangle's base is 5 cm.
- What is the area of the triangle?
- Expected answer: Since the area of a triangle is the base multiplied by the height and divided by 2, then the area of the triangle is \(\frac{5 \times 2}{2}\), which is 5. Therefore, the area of the triangle is 5 cm2, since the unit of area is cm2.
- What is the height of the prism?
- Expected answer: The height of the prism is 8 cm.
- How is the volume of a prism determined?
- Expected answer: The area of the base multiplied by its height.
- What is the volume of your prism?
- Expected answer: Since the height of the prism is 8 cm, then the volume is
\(V = 5 cm^{2} \times 8 cm\)
\(V = 40 cm^{3}\) Therefore, the volume of the prism is 40 cm3.
- Expected answer: Since the height of the prism is 8 cm, then the volume is
- Find or construct a box shaped like a right triangle-based prism (for example, the box of a well-known Swiss chocolate brand).
- Determine the volume of the box.
Source: L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 3: Volume of Large Objects
Goal
In this activity, students will determine the volume of large objects using the most appropriate unit of volume measurement.
Materials
- one metre per team
- one cubic decimetre per team
- a list of objects that are not all prisms (for example, a tree house, a hot water tank, a garbage can, a dictionary, the teacher's desk)
Form teams of two.
Ask students to measure the lengths needed to determine the volume of the objects using the formula they discovered in the previous activities. Students can also construct an object that occupies approximately the same space.
Source: L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 4: Calculate the Height of a Prism from Its Area and Volume
Here are two three-dimensional objects, each with a volume of 126 dm3. Determine the height of each prism.
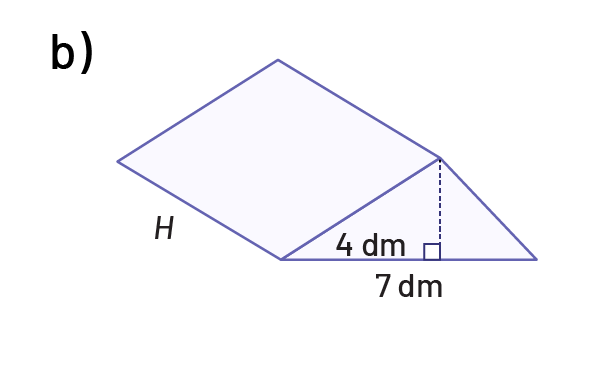
Source: En avant, les maths!, 7e année, ML, Sens de l’espace, p. 21.
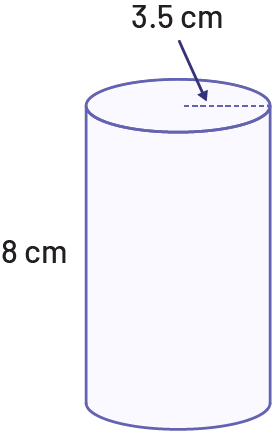
Activity 5: Calculating the Volume of a Cylinder
Find the volume of this cylinder.
A structure is formed by a right trapezoid-based prism topped by a cube. Determine the volume of the structure.
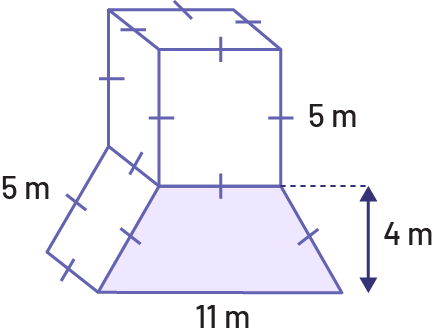
Source: En avant, les maths!, 7e année, ML, Sens de l’espace, p. 22-23.
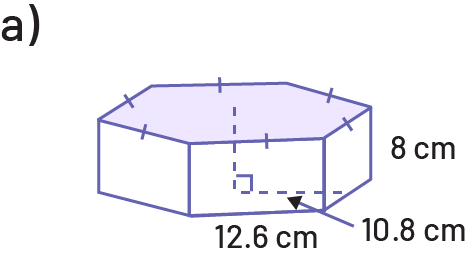
Activity 6: Area and Volume of Three-Dimensional Objects
Determine the area of the base, then the volume of each of the following prisms.
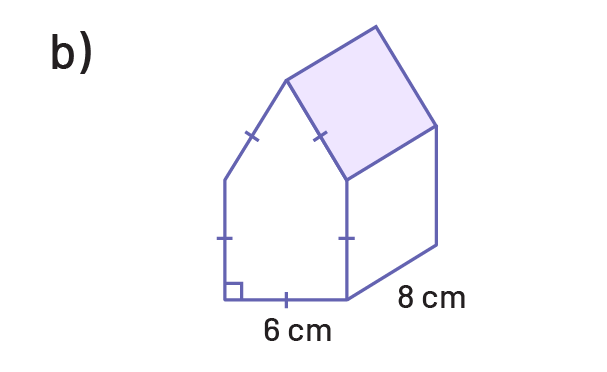
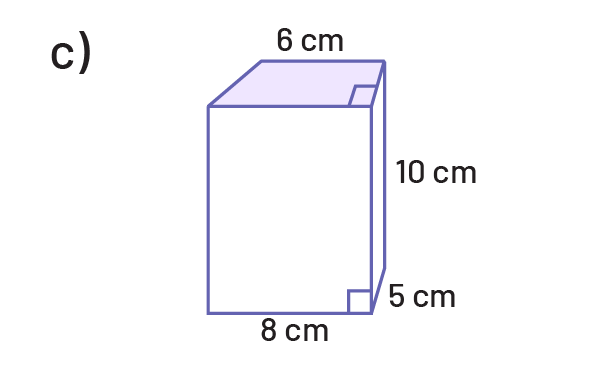
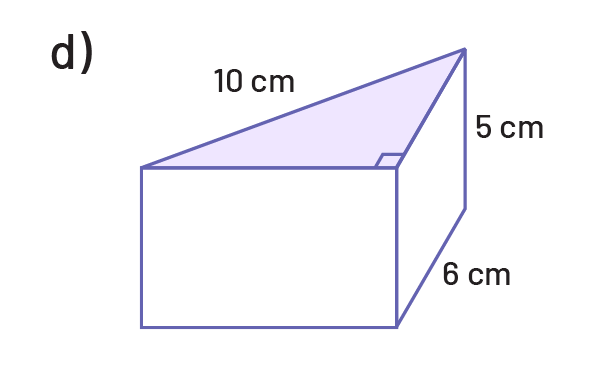
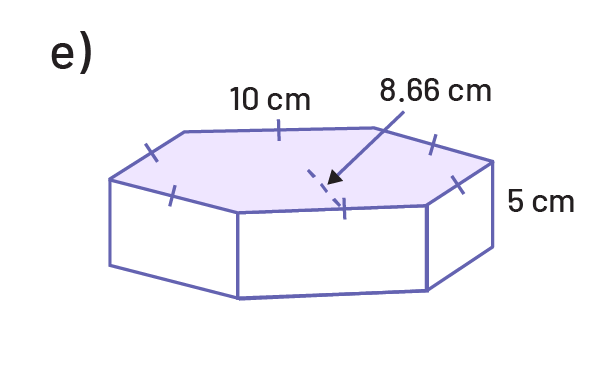
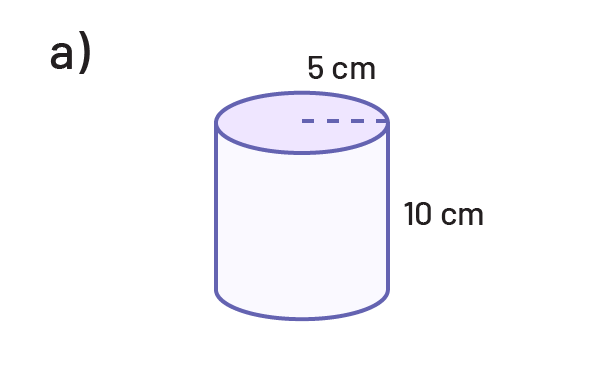
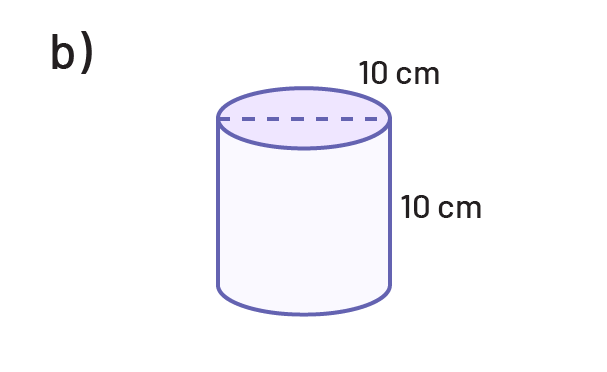
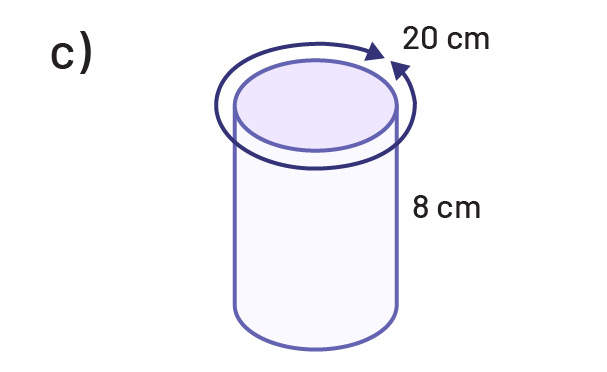
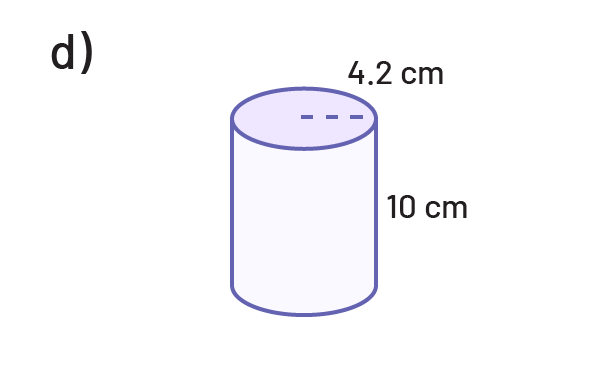
Determine the area of the base and then the volume of each of the following cylinders.
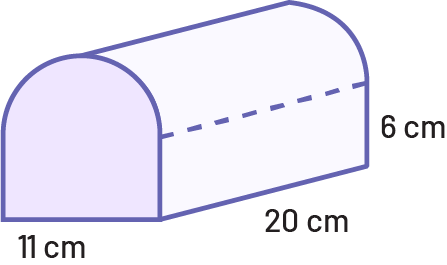
The top of each end of the loaf below is shaped like a half circle. Determine the volume of the loaf. Show your work.
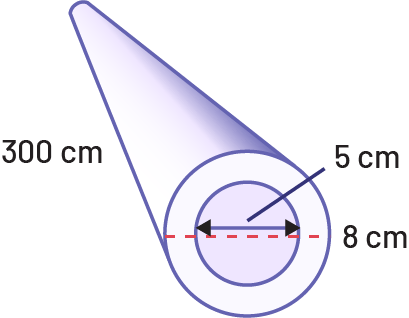
A pipe measuring 300 cm long has an outside diameter of 8 cm and an inside diameter of 5 cm. How much material is needed to make it? Show your work.
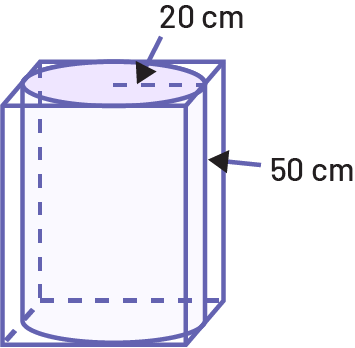
Determine the interior volume of the smallest square-based prism box into which the cylinder below can be inserted.
Source: Réduction des écarts de rendement, 9e année, p. 10-11 et 15-16.