C2.3 Déterminer et utiliser des relations d’équivalence comprenant des nombres naturels jusqu’à 50, dans divers contextes.
Habileté : déterminer et utiliser des relations d’équivalence comprenant des nombres jusqu’à 50
Dans une classe de mathématiques visant à développer la pensée algébrique chez les élèves, l’objectif traditionnel de l’enseignement, soit apprendre à calculer, n’est pas omis; il est largement dépassé.
Développer la pensée algébrique est un cheminement complexe qui mise sur trois processus fondamentaux : abstraire, généraliser et opérer sur l’inconnue.
Note : Bien que les propriétés des opérations, comme la commutativité, soient explorées dans le domaine Nombres, le processus pour arriver à les comprendre et à généraliser relève de la pensée algébrique.
Généraliser
C’est tirer des conclusions valables, vraies dans tous les cas, à partir de l’observation et de l’analyse de quelques exemples (adapté de Squalli, 2002, p. 9).
Dans le cadre de situations d’égalité, les élèves peuvent formuler plus aisément une généralisation lorsque celle-ci se situe à la suite d’un processus de proposition et de vérification d’une conjecture.
Une conjecture est l’expression d’une idée perçue comme étant vraie dans toute situation semblable.
Lorsque les élèves constatent un phénomène récursif en explorant diverses situations d’égalité, elles et ils sont en mesure de proposer une conjecture; par exemple, elles et ils pourraient dire que, si l’on additionne le nombre 0 à un nombre quelconque, la quantité initiale ne change pas.
Les élèves doivent ensuite vérifier si leur conjecture est valable dans d’autres situations semblables. Ainsi, dans la situation de l’exemple précédent, elles et ils pourraient la vérifier avec divers nombres ainsi qu’avec du matériel concret.
Lorsqu’une conjecture semble s’appliquer à toutes les situations semblables, les élèves formulent une généralisation en mots ou à l’aide de symboles.
Exemple
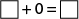
Il y a donc trois étapes importantes dans le processus de généralisation.
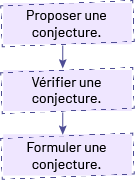
Aux cycles primaire et moyen, les conjectures sont habituellement exprimées en mots. Elles peuvent aussi être représentées à l’aide de matériel concret ou semi-concret afin d’illustrer le plus clairement possible leur raisonnement mathématique.
Le personnel enseignant doit exposer les élèves à diverses situations-problèmes qui les incitent à exercer l’habileté à proposer et à vérifier une conjecture; par exemple, il leur présente la phrase mathématique \(50 +\;6\;–\;6 = 50\) et leur demande ce qu’elles et ils remarquent. Puis, il leur propose la conjecture suivante : « Je me demande, lorsqu’on additionne et que l’on soustrait le même nombre dans une phrase mathématique, si c’est la même chose que lorsqu’on ajoute ou que l’on soustrait zéro. » Le personnel enseignant invite ensuite les élèves à discuter entre elles et eux de cette conjecture et à déterminer si elle est toujours vraie.
Les élèves vérifient cette conjecture avec d’autres phrases mathématiques. Elles et ils ne sont peut-être pas persuadés qu’elle s’applique à n’importe quelle phrase mathématique ou à tous les nombres, notamment aux grands nombres. Au cours des échanges, elles et ils peuvent proposer leurs propres conjectures comme il est illustré ci-dessous.
« Deux
élèves négocient leur raisonnement mathématique. » « Élève un dit » « La phrase mathématique, 100 plus 5 moins 5 égale
100, est vraie parce que si on soustrait un nombre de lui-même, c’est comme si on ne l’avait jamais ajouté. Alors, la
phrase devient 100 est égale à 100. » « Élève 2 » «Je crois que la phrase mathématique est vraie, puisque soustraire
un nombre de lui-même équivaut à l’additionner d’un zéro. La quantité de départ ne change pas. Donc, la phrase
deviendrait cent plus zéro est égale à cent.
Après une vérification de diverses phrases mathématiques, les élèves peuvent conclure que la conjecture est vraie et formuler une généralisation.
Exemple
Comme le vocabulaire des élèves au primaire n’est pas encore très développé et très précis, les premières conjectures doivent habituellement être reformulées ou clarifiées. L’idéal est donc de mettre en pratique la formulation d’une conjecture en groupe-classe, comme le montre l’exemple ci-après. Au cours des échanges, les élèves peuvent souligner les limites de la conjecture qu’a proposée un pair et contribuer à la formulation d’une conjecture commune plus claire et plus pertinente. Il importe cependant que le personnel enseignant établisse un climat d’apprentissage dans lequel les élèves perçoivent les questions des autres comme des interactions positives susceptibles d’alimenter l’échange.
Exemple
Le personnel enseignant présente la phrase mathématique \(34 + 0 = 34\) et demande aux élèves si elle est vraie ou fausse.
- Élève : « Elle est vraie. »
- Le personnel enseignant: « Comment peux-tu l’affirmer? »
- Élève : « Lorsqu’un zéro est ajouté à un nombre, il n’ajoute rien en réalité. On obtient donc le nombre de départ. »
Le personnel enseignant présente d’autres phrases mathématiques semblables. Après plusieurs échanges de ce type, il demande alors aux élèves de formuler une conjecture.
- Élève : « Tous les nombres additionnés d’un zéro restent les mêmes. »
- Autre élève présentant un contre-exemple : « Non, puisque \(10 + 30 = 40\). Les nombres 10 et 30 sont composés de zéros. Additionnés, ils ne restent pas les mêmes. »
Après d’autres échanges, une ou un élève formule une autre conjecture :
- Élève : « Lorsque tu joins un zéro à un autre nombre, tu obtiens l’autre nombre. »
- Autre élève : « C’est faux. »
- Personnel enseignant : « Alors, tu fais référence au nombre qui est juste à côté du zéro? »
- Élève : « Non, additionné à un autre nombre. »
Après maints échanges, la formulation ci-après est retenue : « Zéro, additionné à un autre nombre, est égal à ce nombre. » Lorsque les élèves constatent que cette conjecture s’applique à tous les nombres, elles et ils peuvent généraliser.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 8-11.
Le changement d’une représentation concrète ou semi-concrète à une représentation symbolique, et vice-versa, aide à comprendre les relations d’égalité.
Remarque : La commutativité est un exemple de relation d’équivalence.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année . 2020, Ministère de l’Éducation de l’Ontario.
Habiletés liées aux situations d’équivalence
Au cycle primaire, les élèves développent l’habileté à reconnaître, à expliquer, à créer, à rétablir et à maintenir des situations d’équivalence par l’application de stratégies et de modèles, comme les cadres à 10 cases et la droite numérique. Ces habiletés doivent être développées chaque année d’études en utilisant des nombres de plus en plus grands, en conformité avec les exigences du programme-cadre.
Au début, les situations d’égalité et d’inégalité sont essentiellement explorées oralement et à l’aide de matériel concret. Par la suite, les élèves sont graduellement exposées et exposés à la représentation symbolique; toutefois, le recours au matériel concret demeure tout aussi important et doit s’inscrire conjointement avec les représentations plus abstraites.
Habileté : reconnaître une situation d’équivalence
« L’utilisation efficace du matériel concret favorise l’apprentissage des concepts algébriques, quel que soit le niveau des élèves […]. Puisque cette stratégie fait appel aux sens, entre autres au toucher, à la vue et à l’ouïe, elle leur donne l’occasion de faire la transition entre le concret, le semi-concret, le semi-abstrait et l’abstrait. » (Conseil des écoles catholiques de langue française du Centre-Est, 2003, p. 6)
Dans une démarche de résolution de problèmes, le recours au matériel concret et semi-concret, de même qu’aux modèles, aide les élèves à reconnaître et à représenter des situations d’égalité et d’inégalité.
Exemples
Cadre à dix cases
Droite numérique ouverte double
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 40.
Ce n’est d’ailleurs qu’après avoir manipulé divers modèles à plusieurs reprises dans le même but, soit reconnaître une situation d’égalité ou d’inégalité, que les élèves pourront aborder la représentation purement symbolique (la phrase mathématique) de cette situation. Par ailleurs, pour déterminer la nature de la relation entre les quantités, elles et ils doivent comprendre que les éléments qui figurent de chaque côté du signe = sont des données à analyser et non pas uniquement des expressions à calculer.
Habileté : expliquer une situation d’égalité
« Les élèves ont besoin de discuter de ce qui est égal/inégal, pareil/différent, plus que/moins que, en équilibre/en déséquilibre. C’est par le dialogue authentique qu’elles et ils construisent la signification du concept d’égalité. » [traduction libre] (Taylor-Cox, 2003, p. 17)
Pour développer leur habileté à expliquer une situation d’égalité, les élèves doivent vivre différentes étapes. Le transfert du concret vers la représentation symbolique s’effectue plus aisément lorsque la relation d’égalité se construit en suivant les différentes étapes suivantes.
1. Explorer à l’aide de matériel concret ou semi-concret
Avec des jouets, une ou un élève illustre la situation suivante : l’ajout de 0 jouet à 10 jouets.
2. Décrire à l’aide de mots et de matériel
Si j’ajoute 0 jouet à 10 jouets, la quantité ne changera pas, puisque je n’ajoute rien. Elle sera encore égale à 10 jouets.
3. Représenter à l’aide de symboles
L’élève pourra alors exprimer symboliquement cette égalité en écrivant la phrase mathématique 10 + 0 = 10.
4. Proposer une conjecture
En explorant plusieurs situations semblables, l’élève peut supposer qu’un ajout de 0 ne modifie jamais la quantité.
5. Généraliser pour tous les nombres
Des questions adéquates au cours d’autres situations similaires amènent l’élève à généraliser que l’ajout de 0 à toute quantité ne change pas la quantité.
Les élèves développent aussi leur habileté à expliquer une situation d’égalité en ayant recours à des modèles. En effet, l’utilisation de modèles aide les élèves à communiquer efficacement leur raisonnement.
Exemple
Pour expliquer l’expression 27 + 5 – 5 = 27, les élèves peuvent utiliser une droite numérique ouverte pour appuyer leur raisonnement : « J’effectue un bond de 27 et j’ajoute un bond de 5. Je refais un bond de 5 dans l’autre direction; je reviens donc à 27. C’est comme si je n’avais jamais ajouté un bond de 5. »
Habileté : créer une situation d’égalité
Pour amener les élèves à créer une situation d’égalité, il est important, au début, de leur présenter une situation d’égalité représentée à l’aide de matériel concret. Leur demander de la représenter à l’aide d’une phrase mathématique, de comparer les différentes phrases qu’ont proposées les élèves et de déterminer si elles sont toutes vraies.
Exemples
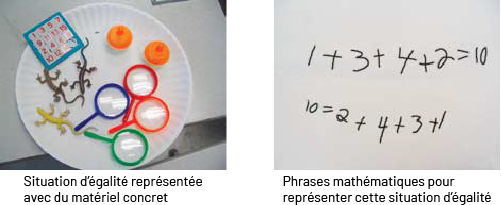Image,
sous-titrée, « Situation d`égalité représentée avec du matériel concret. » Dans une assiette il y a un jeu, 3 reptiles
en plastique, 4 loupes et 2 balles. » Image sous-titrée : « Phrases mathématiques pour représenter cette situation
d’égalité. » Elle se lit comme suit : un plus 3, plus 4, plus 2 égale dix.Puis : dix égale 2, plus 4, plus 3, plus
un.
Par la suite, les élèves peuvent créer leur propre situation d’égalité. Le personnel enseignant leur propose d’écrire des phrases mathématiques et de les représenter en utilisant du matériel concret. Elles et ils doivent avoir l’occasion de créer des situations d’égalité représentées par des phrases mathématiques composées de plus grands nombres afin qu’elles et ils utilisent les propriétés des opérations ou des stratégies au lieu de calculer.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 39-43.
Connaissance : relation d’équivalence
Une relation qui compare des quantités pour montrer qu’elles ont la même valeur.
Exemple
352 est équivalent à 350 et 2.
Connaissance : égalité
Relation entre deux quantités égales.
Connaissance : phrase mathématique
Représentation symbolique qui représente une relation. Dans une phrase mathématique, il n’y a pas d’inconnue ni de variable.
Exemple
Phrases vraies (égales) : \(75 + 5 = 5 + 75\) ou \(50 = 20 + 20 + 10\)
Phrases fausses (inégales) : \(100 = 95 − 5\) ou \(45 + 10 = 15 + 45\)