C1.3 Déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions, et trouver des termes manquants dans des suites représentées à l’aide de formes géométriques et de nombres (suites numériques et non numériques).
Activité 1 : encore des suites!
Sommaire
Dans cette activité, les élèves reproduisent et prolongent des suites non numériques à motif répété à l’aide de matériel de manipulation.
Matériel
- variété de suites créées sur des bandes de papier ou de carton d’environ 30 cm × 5 cm
- matériel de manipulation (en quantité suffisante pour créer chaque suite)
Déroulement
Sur des bandes de papier (par exemple, papier de caisse enregistreuse) ou de carton, préparer des suites à l’aide de
matériel (pâtes alimentaires, boutons, mosaïques géométriques, etc.) que connaissent les élèves. S’assurer que le
motif est répété trois fois. Les objets peuvent être collés sur les bandes ou dessinés. Remettre une suite à chaque
élève ou à chaque équipe ainsi que le matériel pour la reproduire et la prolonger.
Voici quelques exemples de
suites possibles :
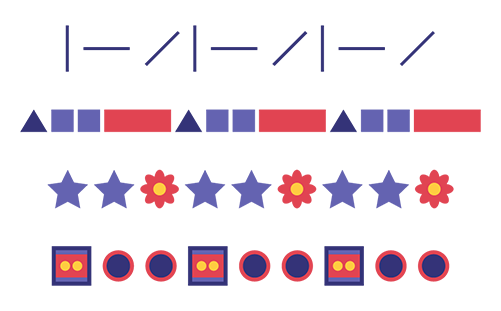 Image 4 types de motifs. Le premier est constitué de lignes. Le motif est vertical, horizontal et
diagonal. Il est répété trois fois. Le motif suivant est celui des formes. Il s'agit d'un triangle bleu, de deux
carrés bleus et d'un rectangle rouge,
répétés trois fois. Le motif suivant contient des étoiles et des fleurs. Le motif est composé de 2 étoiles et d'une
fleur, répétées 3 fois. Enfin, les formes contiennent des contours et des couleurs multiples. Le motif est un carré et
deux cercles répétés trois fois.
Image 4 types de motifs. Le premier est constitué de lignes. Le motif est vertical, horizontal et
diagonal. Il est répété trois fois. Le motif suivant est celui des formes. Il s'agit d'un triangle bleu, de deux
carrés bleus et d'un rectangle rouge,
répétés trois fois. Le motif suivant contient des étoiles et des fleurs. Le motif est composé de 2 étoiles et d'une
fleur, répétées 3 fois. Enfin, les formes contiennent des contours et des couleurs multiples. Le motif est un carré et
deux cercles répétés trois fois.
Demander aux élèves de reproduire la suite sous la bande à l’aide de matériel concret, puis de la prolonger. Les faire travailler au sol, car cela leur permettra de prolonger plus aisément la suite.
Vérifier la façon dont les élèves s’y prennent pour reproduire la suite et la prolonger (par exemple, correspondance un à un, reproduction d’un motif à la fois, explication de la suite).
Observer les élèves et leur poser, au besoin, des questions telles que :
- Peux-tu me décrire ta suite?
- Quel serait le prochain terme de ta suite? Comment le sais-tu?
- Peux-tu me montrer le premier motif?
- Pourquoi dis-tu que c’est le premier élément du motif? le dernier élément?
- Quel est le motif répété dans ta suite?
Lorsque les élèves ont reproduit et prolongé une suite, leur demander d’échanger leur bande ainsi que le matériel pour construire de nouvelles suites.
Circuler, dans la salle de classe, et demander aux élèves de comparer les suites en expliquant les ressemblances et les différences entre les suites reproduites et prolongées (par exemples, attribut, nombre d’éléments composant le motif).
Note : Cette activité se prête bien aux divers thèmes étudiés au cours de l’année. À titre d’exemple, les trois sortes de maisons dans le conte Les trois petits cochons, peuvent être construites et utilisées pour créer une suite.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 86-87.
Activité 2 : bateau à vapeur (prolonger, prédire et justifier)
Construire un bateau à vapeur en utilisant un trapèze rouge et un carré orange. Ajouter un losange bleu pour représenter la vapeur.

Présenter aux élèves le problème suivant : Combien de mosaïques géométriques faut-il pour construire 10 bateaux à vapeur?
La résolution de ce problème permet aux élèves de découvrir la relation entre le nombre de bateaux et le nombre de mosaïques géométriques nécessaires pour les construire. Les élèves de 2e année le résolvent en construisant les bateaux à l’aide de mosaïques géométriques.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 48.
Activité 3 : devine quelle est la suite (prédire et justifier la régularité)
Afin de développer la pensée algébrique chez les élèves, faire cette activité après avoir exploré plusieurs suites numériques à l’aide de matériel concret.
Préparer différents jeux de cartes de nombres pour représenter des suites ayant différentes régularités (par exemple, suite de nombres pairs, de nombres impairs; suite de nombres qui sont des multiples de 5, de 10). Placer les cartes en ordre croissant ou décroissant.
Aligner les cartes d’un jeu, face contre table, devant un petit groupe d’élèves.
Retourner une carte. Demander aux élèves de prédire, à partir de cette carte, le nombre sur la prochaine carte de la suite. Par exemple, la carte retournée porte le nombre 40. Les élèves peuvent prédire que, sur la prochaine carte, il y aura le nombre 50 (règle de régularité de +10), 60 (règle de régularité de +20), 51 (règle de régularité de +11), 30 (règle de régularité de –10), etc.
Retourner la prochaine carte et inviter les élèves à donner la règle de régularité et des caractéristiques de la suite (par exemple, suite croissante ou décroissante) et à nommer les autres termes de la suite sans devoir retourner toutes les cartes.
Une fois toutes les cartes retournées, demander aux élèves d’observer s’il y a une autre règle de régularité; par exemple, selon la suite dévoilée, il est possible qu’il y ait une régularité dans l’augmentation ou la diminution des chiffres des dizaines et des unités.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 65-66.
Activité 4 : Pépé, le cochon
Sommaire
Dans cette activité, les élèves doivent résoudre un problème en découvrant la suite numérique créée selon une régularité.
Matériel
- matériel de manipulation
- grilles de nombres, droites numériques et calendriers (en quantité suffisante pour le groupe-classe)
Déroulement
Présenter aux élèves la situation-problème suivante : Pépé, le cochon de la ferme, aime bien manger des cornichons. S’il en mange deux tous les jours, combien en mange-t-il en 30 jours?
Permettre aux élèves de travailler en équipes de deux ou de trois. Remettre une grande feuille à chaque équipe. Mettre à la disposition des élèves du matériel de manipulation, des grilles de nombres, des droites numériques et des calendriers pour les aider à résoudre le problème.
Circuler, dans la salle de classe, et poser aux élèves des questions telles que :
- Qu’est-ce que tu connais du problème?
- Quelle stratégie vas-tu utiliser pour résoudre le problème?
- Peux-tu expliquer ta stratégie pour résoudre le problème?
Animer un échange mathématique à propos de différentes stratégies utilisées pour résoudre le problème et repérer la régularité (addition de deux cornichons chaque jour).
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 111.
