C2.2 Déterminer ce qui doit être ajouté ou soustrait pour que des expressions comportant des additions et des soustractions deviennent équivalentes.
Activité 1 : rétablir une situation d’égalité à l’aide d’une balance à plateaux
La balance à plateaux est un autre modèle avec lequel les élèves peuvent rétablir l’égalité concrètement, le but étant d’obtenir l’équilibre des plateaux.
Les élèves constatent d’abord l’inégalité. Par exemple :
- Il y a 7 cubes sur un des plateaux alors qu’il y en a 5 sur l’autre. Le plateau qui en contient davantage est plus bas que l’autre.
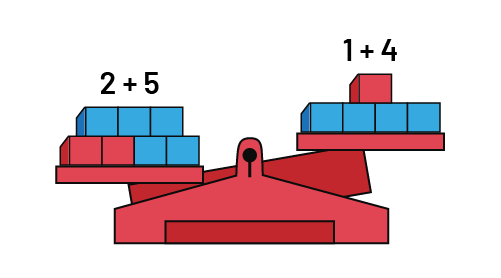 Image Une
balance à plateaux qui contient des blocs. Un côté de la balance contient plus de blocs pour montrer que le nombre est
plus grand. Une expression mathématique figure au-dessus de chaque côté. 2 plus 5 et un plus 4
Image Une
balance à plateaux qui contient des blocs. Un côté de la balance contient plus de blocs pour montrer que le nombre est
plus grand. Une expression mathématique figure au-dessus de chaque côté. 2 plus 5 et un plus 4
Les élèves peuvent ensuite faire appel à l’une ou l’autre des stratégies suivantes :
- Ajouter des cubes, préférablement de couleur différente, un à un, sur le plateau élevé, jusqu’à ce que les deux plateaux soient en équilibre. Au terme de quoi, deux cubes seront ajoutés. Par la suite, représenter la situation symboliquement, soit 2 + 5 = 1 + 4 + 2.
- Retirer un à un 2 cubes du plateau qui en contient 7 pour rétablir l’équilibre et représenter ainsi cette situation symboliquement, soit 2 + 5 - 2 = 1 + 4.
À l’instar de la balance à plateaux, la balance mathématique peut également servir à rétablir une égalité. Dans ce cas, les quantités seront désignées à l’aide de nombres et non d’objets.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 46-47.
Activité 2 : rétablir une relation d’égalité à l’aide de symboles
Rétablir une situation d’égalité à l’aide de symboles : devant une représentation symbolique (phrase mathématique), les élèves doivent s’exercer à appliquer la stratégie comparer des termes pour rétablir l’égalité.
Inciter les élèves, à l’aide de questions, à rétablir l’égalité en explorant les relations qui lient les termes de part et d’autre du symbole de l’égalité.
Exemple
Présenter aux élèves la phrase mathématique 23 + 14 ≠ 14 + 21.
Poser aux élèves les questions suivantes :
- Comment pourriez-vous expliquer la relation entre les nombres qui figurent de chaque côté du signe ≠ (n’est pas égal à)?
Les élèves pourraient répondre : La quantité n’est pas la même de chaque côté du symbole. La situation présente une inégalité parce que 23 + 14 > 14 + 21.
- Que pourriez-vous faire pour rétablir l’égalité?
Les élèves pourraient répondre : Le nombre 14 figure de chaque côté. Le nombre 23, d’un côté, vaut deux de plus que le nombre 21 de l’autre. Le nombre 21, d’un côté, représente deux de moins que le nombre 23 de l’autre. J’ajoute donc 2 au nombre 21 du côté droit pour qu’il soit égal au nombre 23 du côté gauche ou j’enlève 2 au nombre 23 à gauche pour qu’il soit égal au nombre 21 à droite.
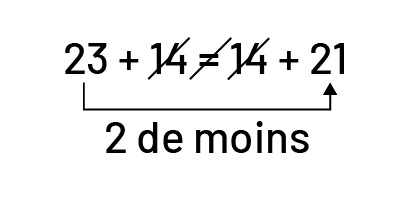
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 47.
Activité 3 : super balançoire à bascule!
Sommaire
Dans cette activité, les élèves explorent des relations pour compléter une situation d’équivalence.
Matériel
- Annexe 1.1, 1.2, 1.3 et 1.4 (une copie par élève)
- Copie des Annexe 1.1 et Annexe 1.3 (tableau blanc interactif)
- ciseaux
- colle
Déroulement
Suivre les étapes suivantes.
Première étape
Afficher, au tableau blanc interactif, la situation d’équivalence 1 présentée à l’Annexe 1.1. Demander aux élèves de décrire la relation entre les masses des acrobates qui est représentée dans cette situation.
- Distribuer aux élèves une copie des Annexe 1.1 et Annexe 1.2. Leur demander de compléter les situations 1a et 1b présentées à l’Annexe 1.1 en respectant la relation entre les masses des acrobates représentée dans la situation d’équivalence 1.
Poser aux élèves les questions suivantes :
- Comment savez-vous que les deux côtés sont équivalents?
- Y a-t-il d’autres solutions possibles?
Au moment de l’objectivation, demander aux élèves d’expliquer leur raisonnement et de justifier leur réponse.
Deuxième étape
Au tableau blanc interactif, afficher la situation d’équivalence 2 présentée à l’Annexe 1.3. Demander aux élèves de décrire la relation entre les masses des acrobates qui est représentée dans cette situation.
Distribuer aux élèves une copie de l’Annexe 1.3 et, au besoin, une autre copie de l’Annexe 1.2. Leur demander de compléter les situations 2a et 2b présentées à Annexe 1.3 en respectant les relations entre les masses des acrobates représentées dans la situation d’équivalence 1 et dans la situation d’équivalence 2.
Poser aux élèves des questions telles que :
- Comment savez-vous que les deux côtés sont équivalents?
- Y a-t-il d’autres solutions possibles?
Au moment de l’objectivation, demander aux élèves d’expliquer leur raisonnement et de justifier leur réponse.
Troisième étape (facultative)
- Distribuer aux élèves une copie de l’annexe 1.4. Les mettre au défi de compléter chacune des situations 3a, 3b et 3c de deux façons différentes.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 142-143 et 145-149.
