C3. Habiletés de codage
Mettre en application ses habiletés en codage pour résoudre des problèmes
et créer des représentations de situations mathématiques de façons computationnelles, à l’aide de concepts et
d’habiletés en codage.
Situation d’apprentissage : À la poursuite des suites!
Durée totale : environ 100 minutes
Sommaire
Dans cette situation d’apprentissage, l’élève utilise la puissance des structures de contrôle imbriquées afin de créer et de prolonger des suites à motif répété et des suites croissantes.
| Attente | Contenus d'apprentissage |
|---|---|
|
C1. Suites et relations Reconnaître, décrire, prolonger et créer une variété de suites, y compris des suites trouvées dans la vie quotidienne, et faire des prédictions à leur sujet. |
C1.1 Reconnaître et décrire des suites à motif répété et des suites croissantes, y compris des suites trouvées dans la vie quotidienne. C1.2 Créer des suites à motif répété et des suites croissantes à l’aide d’une variété de représentations, y compris des tables de valeurs et des représentations graphiques, et établir des liens entre les différentes représentations. |
|
C3. Codage |
C3.1 Résoudre des problèmes et créer des représentations de situations mathématiques de façon computationnelle en écrivant et en exécutant des codes, y compris des codes comprenant des événements séquentiels, simultanés, répétitifs et imbriqués. C3.2 Lire et modifier des codes donnés, y compris des codes comprenant des événements séquentiels, simultanés, répétitifs et imbriqués, et décrire l’incidence des changements sur les résultats. |
| Pratiques pédagogiques à fort impact en mathématiques à privilégier | Description |
|---|---|
| Conversations mathématiques | La mise en situation ci-dessous est l’occasion d’avoir une conversation mathématique avec les élèves du groupe-classe. Cette occasion leur permettra d’échanger leurs idées, de montrer leur compréhension des suites, de raisonner et de prouver leur raisonnement quant au résultat prédit à la suite de la lecture d’un code. Les élèves pourront établir des liens avec des expériences vécues et échanger leurs connaissances relatives aux différentes suites possibles et aux divers événements possibles dans un code. |
| Regroupements flexibles | Les regroupements flexibles au cours de la création ou de la modification de codes facilitent, entre autres, la communication et la collaboration. Les élèves peuvent apprendre les uns des autres et ainsi évoluer leur réflexion mathématique. Tout en tenant compte du profil des élèves, les regroupements peuvent être aléatoires, hétérogènes ou homogènes, selon les besoins. Au cours du déroulement de cette situation d’apprentissage, des regroupements flexibles sont suggérés afin de rendre l’apprentissage optimal pour les élèves. |
| Enseignement en petits groupes | L’enseignement en petits groupes est une pratique pédagogique visant à faire progresser l’apprentissage des élèves. Tout le long de la création ou de la modification d’un code, il est important de former de petits groupes d’élèves afin de leur fournir l’enseignement nécessaire selon les besoins. L’enseignement en petits groupes permet de revoir avec certaines et certains élèves des concepts mathématiques qui appuient leur nouvel apprentissage. Elles et ils pourront donc renforcer leur compréhension des concepts à l’étude. |
| Enseignement explicite | Lorsqu’un code ne donne pas le résultat attendu, le personnel enseignant pourrait demander aux élèves de le lui expliquer. C'est alors un moment propice pour offrir un enseignement explicite relatif à la difficulté observée. Cet enseignement permet de vérifier la compréhension des élèves et de leur fournir une rétroaction immédiate. |
| Connaissances et habiletés préalables | |
|
|
Résultats d’apprentissage
À la fin de cette situation d’apprentissage, l’élève pourra :
- utiliser la terminologie à l’étude telle que code, sprite, événements séquentiels, événements simultanés, événements répétitifs, événements imbriqués, suite à motif répété, motif, suite croissante, table de valeurs;
- décrire des suites;
- créer des suites à motif répété et des suites croissantes en écrivant et en exécutant des codes comprenant des événements séquentiels, des événements simultanés, des événements répétitifs et des événements imbriqués;
- lire et modifier des codes comprenant des événements séquentiels, des événements simultanés, des événements répétitifs et des événements imbriqués.
Critères d’évaluation selon les grilles d’évaluation du rendement
| Compétence | Critère(s) d’évaluation |
|---|---|
| Connaissance et compréhension |
|
| Habiletés de la pensée |
|
| Communication |
|
| Mise en application |
|
Matériel requis
- ordinateur muni d’un logiciel de codage par blocs approprié selon le niveau des élèves
- objets représentant des suites (jetons bicolores, tuiles de couleur, etc.)
- Annexe (Mise en situation)
Note : Les exemples dans cette situation d’apprentissage ont été créés à partir de Scratch.
Vocabulaire mathématique
vocabulaire spécifique au codage (code, sprite, séquence, boucle), événements séquentiels, événements simultanés, événements répétitifs, événements imbriqués, suite à motif répété et suite croissante, motif, terme, rang, table de valeurs
Mise en situation
Durée : environ 20 minutes
L’évaluation peut se faire par les…
Montrer l’image ci-dessous au groupe-classe et animer une discussion de type « je remarque, je me demande ». Prendre en note les remarques et les questions des élèves.

Afficher la table de valeurs ci-dessous à l’écran et demander aux élèves si l’ajout de celle-ci affecte les remarques et les questions échangées lorsqu’on ne voyait que l’image. Ajouter les nouvelles remarques et les nouvelles questions à la liste.
| Mois | Argent ajouté à la tirelire | Somme d’argent dans la tirelire |
|---|---|---|
| Janvier | 5 $ | 5 $ |
| Février | 5 $ | 10 $ |
| Mars | 5 $ | 15 $ |
| Juin | 5 $ | ? |
Exemples de réflexions
- Je remarque que l’on ajoute toujours la même somme à la tirelire.
- Je remarque que l’on saute directement de mars à juin. Il manque des mois.
- Je remarque que la somme d’argent augmente avec le temps.
- Je me demande combien d’argent sera dans la tirelire au mois de juin.
- Je me demande si la somme d’argent restera la même tout le long de l’année.
- Je me demande si la personne dépensera de l’argent de sa tirelire avant le mois de juin.
Fournir aux élèves du matériel de manipulation et leur demander de représenter les données afin de déterminer la somme d’argent dans la tirelire au mois de juin.
Exemple de représentation possible avec des jetons
 = 1$
= 1$
 |
 |
 |
 |
 |
 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| Janvier | Février | Mars | Avril | Mai | Juin |
Vérifier si les prédictions des élèves quant à la somme d’argent dans la tirelire étaient justes. Si des élèves ont obtenu des résultats différents, vérifier si c’est à cause des suppositions qui ont été faites (par exemple, un mois, la personne reçoit plus de 5 $, ou un mois, la personne décide de faire une dépense).
Expliquer aux élèves que la représentation avec du matériel fonctionne relativement bien dans cette situation. Mais, si l’on voulait déterminer les épargnes sur une plus longue durée, cela pourrait prendre beaucoup de temps à représenter. Afin de rendre ce processus plus rapide et convivial, on peut rédiger un code qui généralisera la situation et qui nous permettra de voir les épargnes plus loin dans l’avenir.
Note : Il n’est pas tant question ici de la « réponse », mais plutôt de la représentation de la situation mathématique. Des élèves remarqueront peut-être rapidement que l’on peut multiplier le nombre de mois (le rang) par 5 pour obtenir la somme d’argent épargnée au total. Cependant, cela ne nous montre pas la croissance de la somme d’argent dans la tirelire.
Déroulement
Durée : 60 minutes, en plus du temps alloué à l’exploration du logiciel, au besoin
L’évaluation peut se faire par les…
Présenter aux élèves une séquence de code qui représente la situation de la tirelire. Ne pas leur montrer le résultat de l’exécution du code (ne pas cliquer sur le drapeau vert).
Note : Dans les exemples fournis, les notes en jaune sont des explications du fonctionnement du code et devraient être omises lorsque le code est présenté aux élèves.
Demander aux élèves d’étudier le code afin de prédire ce qu’il fera lorsqu’on l’exécute. La rédaction d’un pseudocode pourrait aussi aider l’élève à prédire le résultat de l’exécution et à mieux comprendre à quoi servent les divers blocs.
Exemple de code représentant le problème de la tirelire à l’aide de jetons
| Code | Résultat de l’exécution |
|---|---|
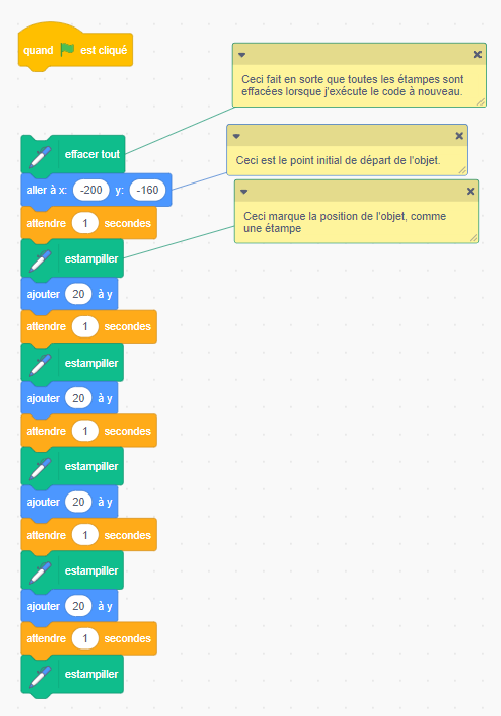 Image Un bloc de code avec trois notes autocollantes correspondant au bloc correspondant. La
première note pointe vers un bloc de correction qui montre un stylo et les mots « effacer tout ». La note
autocollante correspondante se lit « Ceci fait en sorte que toutes les étampes sont effacées lorsque
j'exécute le code de nouveau ». La deuxième note autocollante correspond à un bloc de mouvement qui se lit «
aller à « x » » : et une bulle montrant « moins 200 », « i grec » : et une bulle montrant « moins 160 ». La
note autocollante correspondante se lit « Ceci est le point initial du sprite ». La troisième note
autocollante pointe vers un bloc de corrections qui montre un stylo et les mots « estampiller ». La note
autocollante correspondante indique « Ceci marque la position du sprite comme une étampe ». Image Un bloc de code avec trois notes autocollantes correspondant au bloc correspondant. La
première note pointe vers un bloc de correction qui montre un stylo et les mots « effacer tout ». La note
autocollante correspondante se lit « Ceci fait en sorte que toutes les étampes sont effacées lorsque
j'exécute le code de nouveau ». La deuxième note autocollante correspond à un bloc de mouvement qui se lit «
aller à « x » » : et une bulle montrant « moins 200 », « i grec » : et une bulle montrant « moins 160 ». La
note autocollante correspondante se lit « Ceci est le point initial du sprite ». La troisième note
autocollante pointe vers un bloc de corrections qui montre un stylo et les mots « estampiller ». La note
autocollante correspondante indique « Ceci marque la position du sprite comme une étampe ». |
 |
Exemple d’un pseudocode représentatif du code présenté
| Condition de départ – Drapeau vert |
| Objet : jeton qui se rend au coin inférieur gauche |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
| Objet : jeton qui se déplace vers le haut |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
| Objet : jeton qui se déplace vers le haut |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
| Objet : jeton qui se déplace vers le haut |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
| Objet : jeton qui se déplace vers le haut |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
Après avoir alloué suffisamment de temps aux élèves afin qu’elles et ils fassent leurs prédictions, le code peut être exécuté, et elles et ils pourront comparer leurs prédictions avec le résultat obtenu.
Demander aux élèves ce qui ressort le plus du code qui vient d’être exploré. Il existe plusieurs réponses possibles, mais tenter de diriger le questionnement vers les éléments qui se répètent. Le code, tel qu’il est présenté, est une suite à motif répété. Le motif de la suite est le suivant :
(Déplacement du jeton), (Pause de 1 seconde), (Estampiller)
Ce motif se répète tout le long du code. Celui-ci peut donc être réduit avec une boucle.
Note : Si les élèves ne connaissent pas le concept de boucle, il serait avantageux de leur faire explorer le logiciel de codage en utilisant la boucle afin qu’elles et ils se familiarisent avec cette structure avant de continuer.
Exemple de code réduit avec la boucle
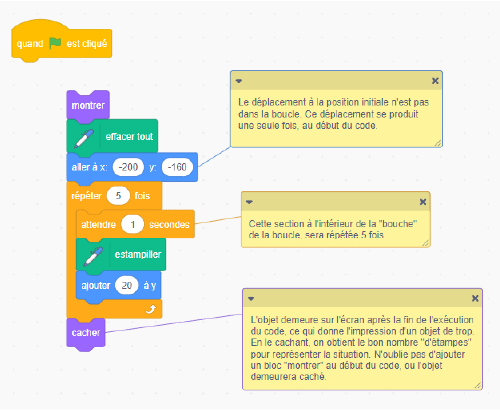 Image Un
bloc de code avec trois notes autocollantes correspondant au bloc respectif. Au-dessus du bloc se trouve un bloc de
contrôle indépendant qui indique « quand » un drapeau vert « est cliqué ». La première note adhésive correspond à un
bloc de mouvement qui se lit « aller à « x » » et une bulle montrant « moins de 200 », « i Greek » et une bulle
montrant « moins 160 ». La note autocollante correspondante se lit « Le déplacement vers la position initiale n'est
pas dans la boucle de déplacement ne se produit qu'une seule fois au début du code ». La deuxième note autocollante
correspond à un bloc de contrôle qui montre la commande « attendre », « un » dans une bulle, « secondes ». La note
autocollante correspondante indique « Cette section à l'intérieur de la « boucle » de la boucle sera répétée 5 fois ».
Enfin, la dernière note autocollante correspond à un bloc d'apparence avec la commande « cacher ». La note
autocollante correspondante se lit « L'objet reste à l'écran après que le code a fini de s'exécuter, donnant
l'impression d'un objet de trop. En le cachant, on obtient le bon nombre de timbres pour représenter la situation.
N'oubliez pas d'ajouter un bloc « montrer » au début du code, sinon l'objet restera caché. »
Image Un
bloc de code avec trois notes autocollantes correspondant au bloc respectif. Au-dessus du bloc se trouve un bloc de
contrôle indépendant qui indique « quand » un drapeau vert « est cliqué ». La première note adhésive correspond à un
bloc de mouvement qui se lit « aller à « x » » et une bulle montrant « moins de 200 », « i Greek » et une bulle
montrant « moins 160 ». La note autocollante correspondante se lit « Le déplacement vers la position initiale n'est
pas dans la boucle de déplacement ne se produit qu'une seule fois au début du code ». La deuxième note autocollante
correspond à un bloc de contrôle qui montre la commande « attendre », « un » dans une bulle, « secondes ». La note
autocollante correspondante indique « Cette section à l'intérieur de la « boucle » de la boucle sera répétée 5 fois ».
Enfin, la dernière note autocollante correspond à un bloc d'apparence avec la commande « cacher ». La note
autocollante correspondante se lit « L'objet reste à l'écran après que le code a fini de s'exécuter, donnant
l'impression d'un objet de trop. En le cachant, on obtient le bon nombre de timbres pour représenter la situation.
N'oubliez pas d'ajouter un bloc « montrer » au début du code, sinon l'objet restera caché. »
À noter que le résultat de ce code donne le même résultat que le code plus long sans la boucle. Faire remarquer aux élèves que le code produit aussi une représentation identique à la figure au rang 1 – Janvier, créée lors de la mise en situation. Leur demander de modifier le code afin qu’il reproduise la situation mathématique de la tirelire. Il existe plusieurs façons de poursuivre.
- Si les élèves commencent leur exploration du codage, il serait avantageux de leur montrer, par essais et erreurs, la façon de modifier le code pour insérer des boucles. En modélisant leurs suggestions, les élèves peuvent travailler ensemble afin de trouver une solution au problème.
- Si les élèves ont un peu plus d'expérience avec le logiciel de codage, des équipes de deux ou même du travail individuel seraient avantageux pour que les élèves découvrent à leur manière des séquences de code qui représenteront la situation mathématique.
- Si le degré d’expérience et d’aisance des élèves varie beaucoup dans le groupe-classe, des regroupements aléatoires ou réfléchies pourraient les mettre dans une situation d’apprentissage par les pairs. Le personnel enseignant pourrait également profiter de cette occasion pour faire de l’enseignement explicite en petits groupes selon les besoins des élèves.
Voici un exemple de pseudocode et de code qui représente la situation de la tirelire avec des boucles
| Condition de départ – Drapeau vert |
| Sprite : jeton qui se rend au coin inférieur gauche (position initiale 1) |
| Répéter 5 fois. |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
| Sprite : jeton qui se déplace vers le haut de 20 unités |
| Sprite : jeton qui retourne à la position initiale 1 |
| Sprite : jeton qui se déplace vers la droite de 30 unités (position initiale 2) |
| Répéter 2 fois. |
| Répéter 5 fois. |
| Pause de 1 seconde |
| La position du jeton est estampillée. |
| Sprite : jeton qui se déplace vers le haut de 20 unités |
| Sprite : jeton qui retourne à la position initiale 2 |
| Sprite : jeton qui se déplace vers la droite de 2 unités |
Ce pseudocode représente 2 mois (position initiale 1 et position initiale 2). En déterminant la tendance, on peut prolonger cette séquence de code, qui ressemble, encore une fois, à une suite, pour représenter plusieurs mois.
| Code | Résultat de l’exécution |
|---|---|
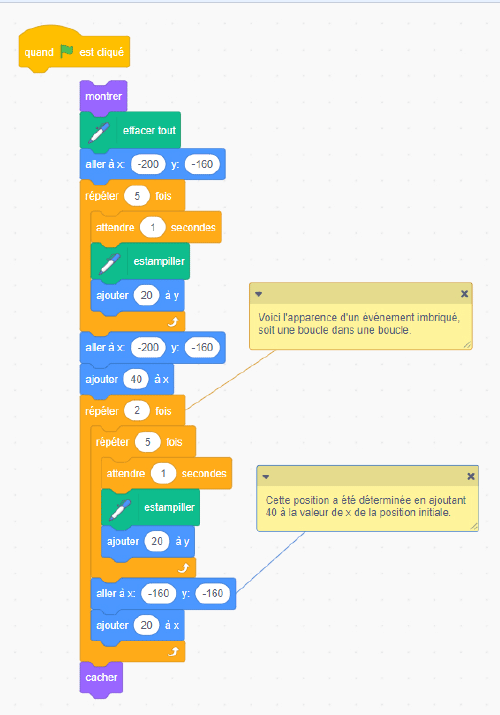 Image Blocs de codage attachés les uns avec les autres : Bloc de départ drapeau vert.
Bloc d‘apparence :
montrer. Bloc de mouvement : « aller à » « x » moins 200 « y » moins 160. Bloc de contrôle : « répéter » 5
fois après les deux blocs suivants. Bloc de contrôle attendre une seconde. Bloc stylo : « estampiller ».
Bloc mouvement : ajouter 20 à « y ». Bloc mouvement : aller à « x » moins 200 « y » moins 160. Bloc de
mouvement : ajouter à « x » 40. Bloc de contrôle : répéter 2 fois. Bloc de contrôle : répéter 5 fois. Bloc
de contrôle : attendre une seconde. Bloc stylo : estampiller. Bloc de mouvement : ajouter 20 à « y ».
Répéter. Bloc de mouvement : aller à « x » moins 160 », « y » moins 160. Bloc de mouvement : ajouter 20 à «
x ». Répéter. Bloc d’apparence : cacher.
Image Blocs de codage attachés les uns avec les autres : Bloc de départ drapeau vert.
Bloc d‘apparence :
montrer. Bloc de mouvement : « aller à » « x » moins 200 « y » moins 160. Bloc de contrôle : « répéter » 5
fois après les deux blocs suivants. Bloc de contrôle attendre une seconde. Bloc stylo : « estampiller ».
Bloc mouvement : ajouter 20 à « y ». Bloc mouvement : aller à « x » moins 200 « y » moins 160. Bloc de
mouvement : ajouter à « x » 40. Bloc de contrôle : répéter 2 fois. Bloc de contrôle : répéter 5 fois. Bloc
de contrôle : attendre une seconde. Bloc stylo : estampiller. Bloc de mouvement : ajouter 20 à « y ».
Répéter. Bloc de mouvement : aller à « x » moins 160 », « y » moins 160. Bloc de mouvement : ajouter 20 à «
x ». Répéter. Bloc d’apparence : cacher.
|
 Image Un grand carré blanc avec 3 rangées de diamants. Chaque rangée contient cinq diamants.
La rangée située dans le coin inférieur gauche le plus éloigné est légèrement distante, tandis que les deux
autres piles sont côte à côte. Image Un grand carré blanc avec 3 rangées de diamants. Chaque rangée contient cinq diamants.
La rangée située dans le coin inférieur gauche le plus éloigné est légèrement distante, tandis que les deux
autres piles sont côte à côte. |
| Observations possibles | Pistes d’interention |
|---|---|
| L’élève ne comprend pas le fonctionnement de la boucle. |
Montrer à l’élève un exemple de code plus simple avec une boucle. Demander à l’élève de rédiger un code avec un seul événement dans une boucle et d’observer le comportement. |
| L’élève ne comprend pas le fonctionnement d’une boucle imbriquée dans une boucle. |
Exécuter le code avec chaque boucle seule afin que l’élève puisse voir son effet sans qu’elle soit imbriquée. Rappeler à l’élève l’effet multiplicatif des boucles imbriquées pour donner un repère plus accessible. |
| L’élève ne reconnaît pas la règle de la suite (rang 1 = une colonne de 5, rang 2 = 2 colonnes de 5, etc.). |
Remettre à l’élève du matériel concret afin de représenter la situation et d’observer la règle. Demander à l’élève de verbaliser ses observations quant à la règle de la suite. Parfois, c’est en conversant que vient la compréhension. |
| Le code de l’élève ne ressemble aucunement au pseudocode rédigé. | Les logiciels de codage utilisent souvent des codes de couleur pour les blocs. Demander à l’élève d’ajouter de la couleur, à l’aide de surligneurs, à son pseudocode en respectant les couleurs utilisées dans le logiciel en question. Le pseudocode et le code peuvent ensuite être comparés afin de trouver les inconsistances. |
| Le code de l’élève ne fonctionne pas. |
Demander à l’élève s’il s’agit d’une erreur de syntaxe (le code ne fonctionne pas du tout) ou d’une erreur de logique (le code fonctionne, mais ne produit pas le résultat désiré). Créer des partenariats de vérification de codes entre les élèves du groupe-classe. Parfois, il est plus facile de trouver une erreur si l’on n’a pas créé le code. Demander à l’élève d’expliquer le rôle de chaque séquence de code, surtout les séquences d’événements imbriqués, avec du pseudocode. |
Objectivation
Durée : 20 minutes
L’évaluation peut se faire par les…
Questionner les élèves sur l’utilisation de la boucle dans la boucle (événements imbriqués).
- Quelles parties du visuel sont le résultat de la boucle interne?
Les cinq objets dans chaque colonne. - Quelles parties du visuel sont le résultat de la boucle externe?
Le nombre de colonnes d’objets par figure. - Qu’arriverait-il si l’on inversait les nombres des répétitions dans la boucle interne et externe de la séquence suivante?
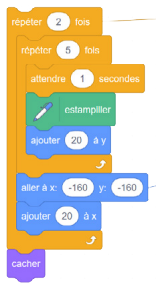 Image Un
bloc de code de répétition qui commence par un bloc qui montre « répéter », « 2 » dans un cercle suivi du mot « fois
». Ce bloc est empilé sur un autre bloc qui montre « répéter », « 5 » dans un cercle suivi du mot « fois ». Puis un
autre bloc de contrôle avec le mot « attendre » puis « un » et le mot « secondes ». Le bloc suivant est un bloc de
corrections qui montre un stylo sur lequel on peut lire « estampiller ». Il est suivi d'un bloc de mouvement
indiquant « ajouter » et d'une bulle indiquant « 20 » et « à », « i grec ». Ce bloc est empilé sur un autre bloc de
mouvement qui montre « aller à « x » » et une bulle montrant « moins 160 », « i grec » et une bulle montrant « moins
160 ». En dessous, un bloc de variables indique « ajouter » et une bulle indique « 20 » puis « à » « x ». La
séquence se termine par un bloc d'apparence avec le mot « cacher ».
Image Un
bloc de code de répétition qui commence par un bloc qui montre « répéter », « 2 » dans un cercle suivi du mot « fois
». Ce bloc est empilé sur un autre bloc qui montre « répéter », « 5 » dans un cercle suivi du mot « fois ». Puis un
autre bloc de contrôle avec le mot « attendre » puis « un » et le mot « secondes ». Le bloc suivant est un bloc de
corrections qui montre un stylo sur lequel on peut lire « estampiller ». Il est suivi d'un bloc de mouvement
indiquant « ajouter » et d'une bulle indiquant « 20 » et « à », « i grec ». Ce bloc est empilé sur un autre bloc de
mouvement qui montre « aller à « x » » et une bulle montrant « moins 160 », « i grec » et une bulle montrant « moins
160 ». En dessous, un bloc de variables indique « ajouter » et une bulle indique « 20 » puis « à » « x ». La
séquence se termine par un bloc d'apparence avec le mot « cacher ».
Au lieu de deux colonnes de cinq objets, on aurait cinq colonnes de deux objets.
Demander aux élèves si cette situation représente un revenu, des épargnes ou un investissement. Les réponses peuvent varier selon l’interprétation du problème. Une discussion sur la terminologie serait utile si ces termes n’ont pas encore été vus en classe.
Réponses possibles
- C’est un revenu mensuel, car la personne s’est fait payer 5 $ par mois, la somme ajoutée à la tirelire.
- Ce sont des épargnes, car la personne choisit de mettre de côté une certaine somme d’argent par mois.
- Ce n’est pas un investissement, la seule chose qui affecte la valeur de la tirelire, ce sont les dépôts de la personne.
Consolidation
Proposer aux élèves différentes situations qu’elles et ils pourraient résoudre à l’aide d’événements imbriqués.
Exemples
- La personne fait les mêmes versements qu’à la situation initiale (versements réguliers de 5 $ par mois), mais dépense 10 $ tous les trois mois.
- La personne dépose plutôt 1 $ de plus par mois (5 $, 6 $, 7 $, 8 $, etc.).
- La personne double la valeur de sa tirelire chaque mois (somme totale dans la tirelire: 5 $, 10 $, 20 $, 40 $).
- Inviter les élèves à retourner dans le logiciel de codage afin de représenter une nouvelle situation de leur choix en se basant sur leur code existant.
- Demander aux élèves de créer des motifs géométriques en utilisant des boucles imbriquées. En utilisant les propriétés d’un rectangle, elles et ils peuvent créer un code qui dessine un rectangle, puis le fait tourner légèrement avant d’en dessiner un autre, un certain nombre de fois. Le code et le motif résultant pourraient ressembler à ceci :
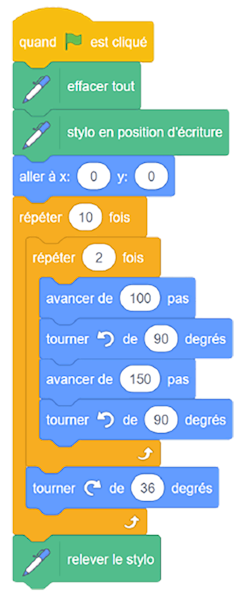 Image Un bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau
vert « est cliqué ».
Empilé sur deux blocs de correction avec une icône de stylo. Le bloc, qui suit la commande de démarrage, est
marqué par la commande « effacer tout ». Le suivant est marqué par « stylo en position d'écriture ». Ces blocs
sont empilés sur un bloc de mouvement qui montre « aller » à « x » et une bulle montrant « zéro », « i
grec » et une bulle montrant « zéro ». Empilés sur un bloc de répétition, commençant par un bloc de contrôle qui
montre « répéter », « 10 » dans un cercle suivi du mot « fois ». Un autre bloc de contrôle qui montre « répéter »,
« 2 » dans un cercle suivi du mot « fois ». Les blocs de mouvement suivant « avancer de » avec une bulle montrant
« cent » et le mot « pas », et un autre bloc de mouvement « tourner » avec une flèche dans le sens inverse des
aiguilles d'une montre puis le mot « de » et une bulle montrant « 90 » suivis du mot « degrés », est imbriqué à
l'intérieur de ce bloc. Deux autres blocs de mouvement sont ajoutés et se lisent « avancer de » avec une bulle
montrant « 150 » et le mot « pas », et un autre bloc de mouvement « tourner » avec une flèche dans le sens inverse
des aiguilles d'une montre puis le mot « de » et une bulle montrant « 90 » suivis du mot « degrés », est imbriqué
à l'intérieur de ce bloc. La boucle est fermée et un dernier bloc de mouvement signale la commande « tourner »
dans le sens des aiguilles d'une montre « de » « 36 » dans une bulle « degrés ». Le bloc est fermé avec le bloc de
correction montrant un stylo marqué « relever le stylo ».
Image Un bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau
vert « est cliqué ».
Empilé sur deux blocs de correction avec une icône de stylo. Le bloc, qui suit la commande de démarrage, est
marqué par la commande « effacer tout ». Le suivant est marqué par « stylo en position d'écriture ». Ces blocs
sont empilés sur un bloc de mouvement qui montre « aller » à « x » et une bulle montrant « zéro », « i
grec » et une bulle montrant « zéro ». Empilés sur un bloc de répétition, commençant par un bloc de contrôle qui
montre « répéter », « 10 » dans un cercle suivi du mot « fois ». Un autre bloc de contrôle qui montre « répéter »,
« 2 » dans un cercle suivi du mot « fois ». Les blocs de mouvement suivant « avancer de » avec une bulle montrant
« cent » et le mot « pas », et un autre bloc de mouvement « tourner » avec une flèche dans le sens inverse des
aiguilles d'une montre puis le mot « de » et une bulle montrant « 90 » suivis du mot « degrés », est imbriqué à
l'intérieur de ce bloc. Deux autres blocs de mouvement sont ajoutés et se lisent « avancer de » avec une bulle
montrant « 150 » et le mot « pas », et un autre bloc de mouvement « tourner » avec une flèche dans le sens inverse
des aiguilles d'une montre puis le mot « de » et une bulle montrant « 90 » suivis du mot « degrés », est imbriqué
à l'intérieur de ce bloc. La boucle est fermée et un dernier bloc de mouvement signale la commande « tourner »
dans le sens des aiguilles d'une montre « de » « 36 » dans une bulle « degrés ». Le bloc est fermé avec le bloc de
correction montrant un stylo marqué « relever le stylo ».
 Image Il s'agit d'une série de dix rectangles. Le point de départ de chaque rectangle est le même.
Le coin inférieur gauche de chaque rectangle est joint au point central. Cette formation donne l'apparence d'une
fleur.
Image Il s'agit d'une série de dix rectangles. Le point de départ de chaque rectangle est le même.
Le coin inférieur gauche de chaque rectangle est joint au point central. Cette formation donne l'apparence d'une
fleur.
Demander aux élèves d’expérimenter en modifiant le nombre de répétitions de la boucle extérieure et le nombre de degrés de rotation à chaque répétition afin de créer de nouveaux motifs.
Liens avec les autres domaines mathématiques
Nombres
B2.2 Se rappeler les faits de multiplication de 1 × 1 à 10 × 10 et les faits de division associés, et démontrer sa compréhension de ces faits.
Les boucles imbriquées créent des représentations de multiplications plus complexes qu’avec des boucles simples. On peut, par exemple, obtenir 24 répétitions d’une séquence de code en le plaçant dans une boucle de 4 répétitions, et placer la boucle de 4 répétitions dans une boucle de 6 répétitions.
Algèbre
C1.1 Reconnaître et décrire des suites à motif répété et des suites croissantes, y compris des suites trouvées dans la vie quotidienne.
C1.2 Créer des suites à motif répété et des suites croissantes à l’aide d’une variété de représentations, y compris des tables de valeurs et des représentations graphiques, et établir des liens entre les différentes représentations.
C2.1 Déterminer et utiliser des symboles comme variables dans des expressions et des équations.
Les événements imbriqués créent des suites croissantes. Une première boucle définit le motif de la suite, et on la place dans une deuxième boucle qui détermine le nombre de répétitions. Par la suite, il s’agit d’ajouter des blocs de code et des variables pour modifier la règle de la suite.
Sens de l’espace
E2.5 Utiliser la structure en rangées et en colonnes d’une disposition rectangulaire pour mesurer l’aire d’un rectangle et pour démontrer que l’aire d’un rectangle peut être calculée en multipliant sa base par sa hauteur.
Les boucles imbriquées peuvent aider à représenter la disposition rectangulaire. La boucle interne représente le nombre d’éléments dans une rangée, et la boucle externe, le nombre de rangées.
Littératie financière
F1.3 Expliquer les concepts de dépense, d’épargne, de revenu, d’investissement et de don, et déterminer les principaux éléments à considérer dans la prise de décisions simples.
Différenciation pédagogique et conception universelle de l’apprentissage
L’élève qui est à l’aise avec le codage en blocs pourrait utiliser des variables afin d’automatiser encore plus le code. Voir ci-dessous un exemple de code qui demande le nombre de mois à représenter. L’élève utilise la réponse afin de représenter la situation mathématique. Le code pourrait aussi être étudié afin de prédire le résultat ou fourni afin que l'élève le modifie selon ses objectifs personnels.
| Code | Résultat de l’exécution |
|---|---|
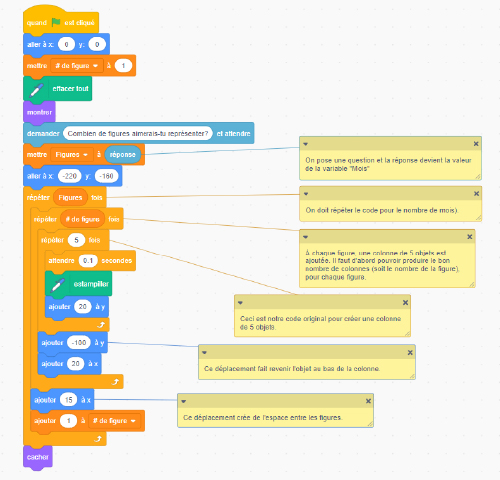 Image Un bloc de code avec les six notes autocollantes correspondantes. La première note
correspond à un bloc de contrôle qui montre « mettre » le mot « mois » dans une bulle avec une flèche
descendante et « à » « réponse ». La note autocollante correspondante « on pose une question, et la réponse
devient la valeur de la variable « Mois » . La deuxième note autocollante pointe vers un bloc de contrôle
qui se lit « répéter » avec le mot « Mois » dans une bulle avec une flèche descendante et « fois ». La note
autocollante correspondante indique « On doit répéter le code pour le nombre de mois voulu ». La troisième
note autocollante correspond à un bloc qui se lit « répéter » avec le mot « Mois » dans une bulle avec une
flèche descendante et « fois ». La note autocollante correspondante se lit « À chaque figure, une colonne de
5 objets est ajoutée. Le rang de la figure détermine le nombre de colonnes de 5 objets ». La quatrième note
autocollante correspond à un autre contrôle marqué « répéter » et à une bulle avec « 5 » et le mot « fois ».
La note autocollante correspondante se lit comme suit : « Ceci est code original pour créer une colonne de 5
objets ». La cinquième note autocollante correspond à un bloc de mouvement qui se lit « ajouter » « 20 »
dans une bulle et « à » suivi de « i grec ». La note autocollante correspondante se lit « Ce déplacement
faire revenir l'objet au bas de la colonne ». Enfin, la dernière note autocollante correspond à un bloc de
mouvement qui se lit « ajouter » « 8 » dans une bulle et « à » suivi de « x ». La dernière note autocollante
se lit « Ce déplacement crée de l'espace entre les rangs ». Image Un bloc de code avec les six notes autocollantes correspondantes. La première note
correspond à un bloc de contrôle qui montre « mettre » le mot « mois » dans une bulle avec une flèche
descendante et « à » « réponse ». La note autocollante correspondante « on pose une question, et la réponse
devient la valeur de la variable « Mois » . La deuxième note autocollante pointe vers un bloc de contrôle
qui se lit « répéter » avec le mot « Mois » dans une bulle avec une flèche descendante et « fois ». La note
autocollante correspondante indique « On doit répéter le code pour le nombre de mois voulu ». La troisième
note autocollante correspond à un bloc qui se lit « répéter » avec le mot « Mois » dans une bulle avec une
flèche descendante et « fois ». La note autocollante correspondante se lit « À chaque figure, une colonne de
5 objets est ajoutée. Le rang de la figure détermine le nombre de colonnes de 5 objets ». La quatrième note
autocollante correspond à un autre contrôle marqué « répéter » et à une bulle avec « 5 » et le mot « fois ».
La note autocollante correspondante se lit comme suit : « Ceci est code original pour créer une colonne de 5
objets ». La cinquième note autocollante correspond à un bloc de mouvement qui se lit « ajouter » « 20 »
dans une bulle et « à » suivi de « i grec ». La note autocollante correspondante se lit « Ce déplacement
faire revenir l'objet au bas de la colonne ». Enfin, la dernière note autocollante correspond à un bloc de
mouvement qui se lit « ajouter » « 8 » dans une bulle et « à » suivi de « x ». La dernière note autocollante
se lit « Ce déplacement crée de l'espace entre les rangs ». |
 Image Un grand carré avec des rangées de diamants. Chaque rangée contient cinq diamants
empilés verticalement. Les rangées sont groupées par ordre croissant de gauche à droite. La première rangée
contient une colonne, puis 2, 3, 4, 5, 6 colonnes de cinq diamants par rangée. Image Un grand carré avec des rangées de diamants. Chaque rangée contient cinq diamants
empilés verticalement. Les rangées sont groupées par ordre croissant de gauche à droite. La première rangée
contient une colonne, puis 2, 3, 4, 5, 6 colonnes de cinq diamants par rangée. |
L’élève qui a de la difficulté à utiliser le logiciel de codage pourrait faire équipe avec des élèves plus à l’aise afin d’apprendre de ses partenaires. Un groupe d’élèves ayant le même degré d’expérience avec le logiciel faciliterait aussi l’enseignement explicite selon les besoins du groupe.
Plusieurs logiciels de codage permettent le partage de projets. Les élèves pourraient recevoir à l’avance certaines séquences de blocs de code assemblés afin de les mettre aux bons endroits pour faire fonctionner le code.
Exemple
| L'élève commence par ceci… | … en vue de créer ceci |
|---|---|
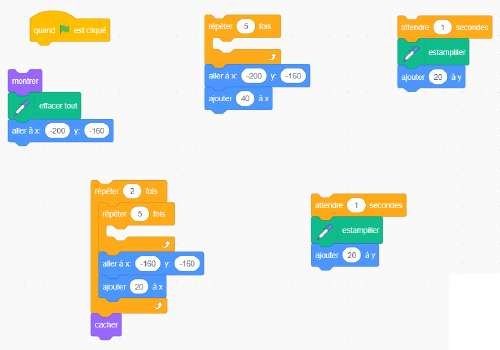 Image Cinq petits blocs de code. Le premier bloc de code commence par un bloc de
contrôle qui montre «
quand » un drapeau vert « est cliqué ». Il est empilé sur un bloc d'apparence avec le mot « montrer ». Ce
bloc est empilé sur un bloc de correction montrant un stylo marqué « effacer tout ». Enfin un bloc de
mouvement qui montre « aller à « x » » : et une bulle montrant « moins 200 », « i grec » et une bulle
montrant « moins 160 ». Les blocs suivants commencent tous par des blocs de contrôle. Le bloc suivant
commence la séquence par un
bloc de contrôle qui montre « répéter », « 5 » dans un cercle suivi du mot « fois ». Il est empilé sur des
motions qui montrent « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une bulle montrant
« moins 160 ». Et se termine par un autre bloc variable marqué « ajouter » et une bulle montrant « 40 » puis
« à » « x ». En dessous, un autre bloc de code. Le prochain à être empilé est un bloc de contrôle marqué «
répéter », «
2 » dans un cercle suivi du mot « fois ». Empilé sur un autre bloc de contrôle marqué « répéter », « 6 »
dans un cercle suivi du mot « fois ». Ceci sur un bloc de mouvement montre « aller à « x » » et une bulle
montrant « moins 150 », « i grec » et une bulle montrant « moins 160 ». Ce bloc est empilé sur un bloc
variable marqué « ajouter » et une bulle montrant « 20 » et ensuite « à » « x ». Le contrôle affiche une
flèche dans le sens inverse des aiguilles d'une montre et la séquence se termine par un bloc d'apparence
avec le mot « cacher ». Le bloc suivant glisse entre le deuxième bloc. La séquence commence par un bloc de
contrôle marqué «
attendre » puis « un » et le mot « secondes ». Vient ensuite un bloc de correction montrant un stylo marqué
« estampiller ». Elle se termine par un bloc variable « ajouter » et une bulle indiquant « 20 » puis « à » «
i grec ». Le dernier bloc se glisse dans le troisième bloc. Il commence par le bloc de contrôle « attendre »
puis «
un » et le mot « secondes ». Suivi du bloc de correction montrant un stylo marqué « estampiller ». Et la
boucle est fermée par un bloc variable montrant « ajouter » et une bulle montrant « 20 » puis « à » « i grec
».
Image Cinq petits blocs de code. Le premier bloc de code commence par un bloc de
contrôle qui montre «
quand » un drapeau vert « est cliqué ». Il est empilé sur un bloc d'apparence avec le mot « montrer ». Ce
bloc est empilé sur un bloc de correction montrant un stylo marqué « effacer tout ». Enfin un bloc de
mouvement qui montre « aller à « x » » : et une bulle montrant « moins 200 », « i grec » et une bulle
montrant « moins 160 ». Les blocs suivants commencent tous par des blocs de contrôle. Le bloc suivant
commence la séquence par un
bloc de contrôle qui montre « répéter », « 5 » dans un cercle suivi du mot « fois ». Il est empilé sur des
motions qui montrent « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une bulle montrant
« moins 160 ». Et se termine par un autre bloc variable marqué « ajouter » et une bulle montrant « 40 » puis
« à » « x ». En dessous, un autre bloc de code. Le prochain à être empilé est un bloc de contrôle marqué «
répéter », «
2 » dans un cercle suivi du mot « fois ». Empilé sur un autre bloc de contrôle marqué « répéter », « 6 »
dans un cercle suivi du mot « fois ». Ceci sur un bloc de mouvement montre « aller à « x » » et une bulle
montrant « moins 150 », « i grec » et une bulle montrant « moins 160 ». Ce bloc est empilé sur un bloc
variable marqué « ajouter » et une bulle montrant « 20 » et ensuite « à » « x ». Le contrôle affiche une
flèche dans le sens inverse des aiguilles d'une montre et la séquence se termine par un bloc d'apparence
avec le mot « cacher ». Le bloc suivant glisse entre le deuxième bloc. La séquence commence par un bloc de
contrôle marqué «
attendre » puis « un » et le mot « secondes ». Vient ensuite un bloc de correction montrant un stylo marqué
« estampiller ». Elle se termine par un bloc variable « ajouter » et une bulle indiquant « 20 » puis « à » «
i grec ». Le dernier bloc se glisse dans le troisième bloc. Il commence par le bloc de contrôle « attendre »
puis «
un » et le mot « secondes ». Suivi du bloc de correction montrant un stylo marqué « estampiller ». Et la
boucle est fermée par un bloc variable montrant « ajouter » et une bulle montrant « 20 » puis « à » « i grec
».
|
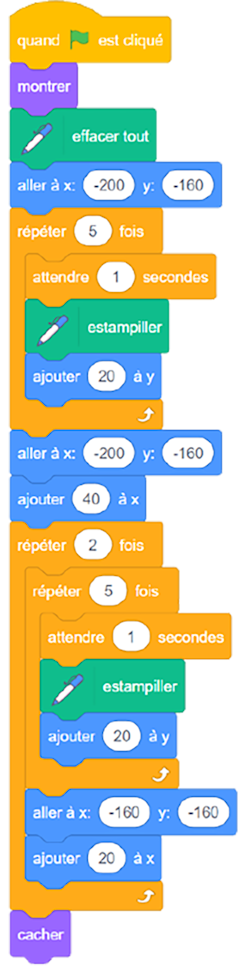 Image Le premier bloc de code commence par un bloc de contrôle qui montre « quand » un
drapeau vert « est cliqué ». Il est empilé sur un bloc d'apparence avec le mot « montrer ». Ce bloc est
empilé sur un bloc de correction montrant un stylo marqué « effacer tout ». Enfin un bloc de mouvement qui
montre « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une bulle montrant « moins 160
». Le bloc suivant commence la séquence par un bloc de contrôle qui montre « répéter », « 5 » dans un cercle
suivi du mot « fois ». La séquence continue par un bloc de contrôle marqué « attendre » puis « un » et le
mot « secondes ». Vient ensuite un bloc de correction montrant un stylo marqué « estampiller ». Elle se
termine par un bloc variable « ajouter » et une bulle indiquant « 20 » puis « à » « i grec ». Il est empilé
sur des motions qui montrent « aller à « x » »et une bulle montrant « moins 200 », « i grec » et une bulle
montrant « moins 160 ». Et se termine par un autre bloc variable marqué « ajouter » et une bulle montrant «
40 » puis « à » « x ». Le prochain à être empilé est un bloc de contrôle marqué « répéter », « 2 » dans un
cercle suivi du mot « fois ». Empilé sur un autre bloc de contrôle marqué « répéter », « 6 » dans un cercle
suivi du mot « fois ». Un bloc de contrôle « attendre » puis « un » et le mot « secondes » suit. Suivi du
bloc de correction montrant un stylo marqué « estampiller ». Et la boucle est fermée par un bloc variable
montrant « ajouter » et un une bulle montrant « 20 » puis « à » « i grec ». La séquence se poursuit avec un
bloc de mouvement montre « aller à « x » » et une bulle montrant « moins 150 », « i grec » et une bulle
montrant « moins 160 ». Ce bloc est empilé sur un bloc variable marqué « ajouter » et une bulle montrant «
20 » et ensuite « à » « x ». Le contrôle affiche une flèche dans le sens inverse des aiguilles d'une montre
et la séquence se termine par un bloc d'apparence avec le mot « cacher ». Image Le premier bloc de code commence par un bloc de contrôle qui montre « quand » un
drapeau vert « est cliqué ». Il est empilé sur un bloc d'apparence avec le mot « montrer ». Ce bloc est
empilé sur un bloc de correction montrant un stylo marqué « effacer tout ». Enfin un bloc de mouvement qui
montre « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une bulle montrant « moins 160
». Le bloc suivant commence la séquence par un bloc de contrôle qui montre « répéter », « 5 » dans un cercle
suivi du mot « fois ». La séquence continue par un bloc de contrôle marqué « attendre » puis « un » et le
mot « secondes ». Vient ensuite un bloc de correction montrant un stylo marqué « estampiller ». Elle se
termine par un bloc variable « ajouter » et une bulle indiquant « 20 » puis « à » « i grec ». Il est empilé
sur des motions qui montrent « aller à « x » »et une bulle montrant « moins 200 », « i grec » et une bulle
montrant « moins 160 ». Et se termine par un autre bloc variable marqué « ajouter » et une bulle montrant «
40 » puis « à » « x ». Le prochain à être empilé est un bloc de contrôle marqué « répéter », « 2 » dans un
cercle suivi du mot « fois ». Empilé sur un autre bloc de contrôle marqué « répéter », « 6 » dans un cercle
suivi du mot « fois ». Un bloc de contrôle « attendre » puis « un » et le mot « secondes » suit. Suivi du
bloc de correction montrant un stylo marqué « estampiller ». Et la boucle est fermée par un bloc variable
montrant « ajouter » et un une bulle montrant « 20 » puis « à » « i grec ». La séquence se poursuit avec un
bloc de mouvement montre « aller à « x » » et une bulle montrant « moins 150 », « i grec » et une bulle
montrant « moins 160 ». Ce bloc est empilé sur un bloc variable marqué « ajouter » et une bulle montrant «
20 » et ensuite « à » « x ». Le contrôle affiche une flèche dans le sens inverse des aiguilles d'une montre
et la séquence se termine par un bloc d'apparence avec le mot « cacher ». |
Source : Guide d’enseignement efficace des mathématiques, Codage, p. 88-103.
