C2.4 Résoudre des inégalités qui comprennent deux opérations et des nombres naturels jusqu’à 100, et vérifier et présenter les solutions à l’aide de modèles et de représentations graphiques.
Activité 1 : résolution d’inégalité large
Demander aux élèves de résoudre l’inégalité \( 5x + 50 \leq 100 \) et de vérifier leur solution à l’aide d’une droite numérique.
Stratégie
Représentation de cette inégalité à l’aide d’une droite numérique
Je dois d’abord isoler la variable x.
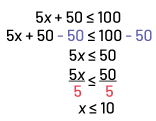 Image 5 « x » plus 50 plus petit ou égal à 100. 5 « x » plus 50 moins 50 plus petit ou égal 100
moins 50. 5 « x » plus petit ou égal à 50. 5 « x « sur 5 plus petit ou égal à 50 sur 5. « x » plus petit ou égal à
dix.
Image 5 « x » plus 50 plus petit ou égal à 100. 5 « x » plus 50 moins 50 plus petit ou égal 100
moins 50. 5 « x » plus petit ou égal à 50. 5 « x « sur 5 plus petit ou égal à 50 sur 5. « x » plus petit ou égal à
dix.
Puisque l’équation représente une relation d’inégalité large (« est inférieure ou égale à »), je peux dessiner un point sur le nombre 10, la droite fléchée vers la gauche pour montrer les résultats « 10 et tous les nombres inférieurs ou égaux à 10 ».

Les valeurs possibles de x sont les nombres naturels inférieurs ou égaux à 10, soit 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 et 0.
Source : En avant, les maths!, 6e année, CM, Algèbre, p. 3.
Activité 2 : résolution d’inégalité stricte
Demander aux élèves de résoudre l’inégalité \(2m + 38 < 90 \) et de vérifier leur solution à l’aide d’une droite numérique.
Stratégie
Représentation à l’aide d’une droite numérique
Pour représenter cette inégalité sur une droite numérique, je dois d’abord isoler la variable m.
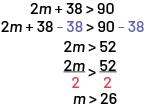 Image 2 « m » plus 38 plus grand que 90. 2 « m » plus 38 moins 38, plus grand que 90 moins 38. 2 « m » plus grand que 52. 2 « m » sur 2, plus grand que 52 sur 2. « m » plus grand que 26.
Image 2 « m » plus 38 plus grand que 90. 2 « m » plus 38 moins 38, plus grand que 90 moins 38. 2 « m » plus grand que 52. 2 « m » sur 2, plus grand que 52 sur 2. « m » plus grand que 26.

Je dessine une droite et j’utilise le cercle, sur le nombre 26, pour indiquer que la relation d’inégalité est stricte (« est supérieure à » 26). Les valeurs possibles de m sont les nombres naturels supérieurs à 26, soit 27, 28, 29, etc.
Source : En avant, les maths!, 6e année, CM, Algèbre, p. 4.
Activité 3 : Travailler pour se gâter!
Présenter aux élèves le problème suivant :
Erykah a trouvé trois paires de chaussures de course qui lui plaisent, coûtant 50 $, 59 $ et 79 $. Elle a déjà économisé 31 $. Elle travaille pour un service de promenade de chiens qui la paie 15 $ par heure. Combien d’heures devra-t-elle travailler pour acheter n’importe laquelle de ces paires de souliers? Représentez votre solution sur une droite numérique.
Encourager les élèves à travailler en équipes pour résoudre le problème.
Exemple
Représenter le problème sous forme d’équation algébrique :
Erykah gagne 15 $ x h, où h représente le nombre d’heures travaillées.
La première paire de chaussures coûte 50 $, et Erykah a déjà économisé 31 $. Donc, pour acheter ces chaussures, Erykah doit avoir 50 $ − 31 $.
Pour trouver le nombre d’heures qu’Erykah devra travailler pour acheter la première paire de chaussures, l’équation algébrique est :
15 x h ≥ 50 – 31
15 x h ≥ 19
| h | 15 x h | ≥ 19 |
|---|---|---|
| 0 | 0 | non |
| 1 | 15 | non |
| 2 | 30 | oui |
| 3 | 45 | oui |
15 x h ≥ 19
15 x 2 ≥ 19
Erykah doit travailler 2 heures.
Demander à quelques équipes de présenter leur solution. Permettre aux élèves de réviser leur réponse.
