C2.3 Résoudre des équations qui comprennent des termes multiples et des nombres naturels dans divers contextes, et vérifier les solutions.
Habileté : résoudre des équations
Différents types d’équations
L’équation est une façon symbolique de représenter une relation qui peut être difficile à comprendre, entre autres, parce qu’il existe divers types d’équations dont la fonction varie selon la situation. Au cycle moyen, les élèves rencontrent quatre types d’équations :
Équation à résoudre : Une équation comme 2 + n = 14 doit être résolue. Elle provient habituellement d’une situation-problème et décrit une relation d’égalité. La lettre n représente une valeur inconnue qui doit être déterminée.
Équation qui représente une relation entre deux quantités changeantes : Une équation comme c = 2r + 3 sert à exprimer une relation; par exemple, la relation entre le rang d’une figure (r) dans une suite non numérique et le nombre de cure-dents (c) qui la composent. Les lettres r et c sont des variables, puisqu’elles peuvent prendre diverses valeurs.
Équation qui sert de formule : Pour calculer l’aire (A) d’un carré, on peut utiliser l’équation A = c × c. On appelle une telle équation une formule, puisqu’on l’utilise pour calculer l’aire d’un carré ayant des côtés de longueur c. On ne résout pas une telle équation.
Équation qui généralise une situation d’égalité : On peut généraliser la relation d’égalité entre l’addition de deux nombres identiques quelconques et la multiplication de ce nombre par 2, comme 4 + 4 = 2 × 4, par l’équation n + n = 2 × n. On ne résout pas une telle équation, et il ne s’agit pas d’une formule. De plus, elle ne représente pas une relation entre deux quantités changeantes.
Chacun de ces types d’équations est examiné plus en détail dans ce qui suit.
Note : Les précisions quant aux divers types d’équations sont données afin de reconnaître que les concepts algébriques ne sont pas rencontrés et traités exclusivement dans le cadre d’activités en modélisation et en algèbre; par exemple, on trouve régulièrement des équations qui servent de formules dans le domaine Mesure. Cependant, au cycle moyen, les élèves n’ont pas nécessairement à faire la distinction entre ces types d’équations.
Équation à résoudre
Les élèves prennent connaissance de ce type d’équation au cycle primaire, habituellement dans un contexte de modélisation et d’algèbre, ainsi que dans un contexte de numération et sens du nombre. Elles proviennent de situations-problèmes, et la résolution de ces équations se fait souvent au moyen de représentations concrètes et d’illustrations.
Au cycle moyen, les élèves sont davantage exposées et exposés aux équations à résoudre. Il est essentiel qu’elles et ils maîtrisent la notion d’égalité comme expression d’équilibre avant qu’elles et ils ne commencent à résoudre ces équations. De plus, il importe que ces équations proviennent de situations-problèmes afin que les élèves puissent donner un sens aux équations et à leur solution.
Résoudre de telles équations signifie déterminer la valeur de la variable qui maintient l’égalité. La résolution d’équations doit s’effectuer dans un contexte de compréhension et d’analyse de l’égalité. Il est alors important d’inviter régulièrement les élèves à expliquer leur démarche de résolution, à justifier leurs gestes et à montrer leur compréhension des concepts présents afin d’éviter que la résolution d’équations ne devienne qu’une application aveugle de procédures.
Résolution d’équations par essais systématiques
Selon cette stratégie élémentaire, les élèves choisissent de façon systématique des valeurs potentielles de variable jusqu’à ce qu’une de ces valeurs rende l’égalité vraie; par exemple, pour résoudre l’équation 2 × p + 6 = 22, elles et ils choisissent successivement p = 1, 2, 3… et constatent que l’égalité est vraie lorsque p = 8.
Pour résoudre certaines équations, comme 125 − b = 32, les élèves peuvent utiliser des stratégies qui font appel à leur sens du nombre de manière à diminuer le nombre d’essais. Ainsi, pour résoudre cette équation, il ne serait pas sage de procéder en utilisant b = 1, b = 2, b = 3, et ainsi de suite, car cela prendrait beaucoup trop de temps. Ils pourraient penser comme suit : « Je sais que 125 – 100 = 25, et 25 est près de 32. Si je soustrais 105, j’obtiens 20. Je m’éloigne de la quantité recherchée. Donc, je vais soustraire un peu moins que 100. Je vais essayer b = 99, b = 98, et ainsi de suite. »
Avantages de la résolution d’équations par essais systématiques :
- Les élèves mettent en évidence ce que signifie résoudre une équation, c’est-à-dire déterminer la valeur de la variable qui maintient l’égalité.
- Les élèves travaillent de façon systématique et non de façon aléatoire. Elles et ils peuvent aussi faire appel à leur sens du nombre.
Inconvénient de la résolution d’équations par essais systématiques :
- La communication du travail effectué peut être désorganisée, car il peut être difficile de laisser des traces des essais. On peut alors inciter les élèves à garder de telles traces en créant une table de valeurs.
Voici un exemple d’une table de valeurs utilisée pour résoudre l’équation 125 − b = 32 :
| b | 100 | 105 | 99 | 98 | 95 | 93 |
|---|---|---|---|---|---|---|
| 125 – b | 25 | 20 | 26 | 27 | 30 | 32 |
Note : Certaines notations doivent être évitées; par exemple, pour résoudre l’équation 2 × p + 6 = 22,
l’élève qui essaie p = 1 ne doit pas écrire 2 × 1 + 6 = 22, puisque cette égalité est fausse. Elle ou il peut
évaluer le membre de gauche pour obtenir 2 × 1 + 6 = 8 ou utiliser l’équation sous la forme interrogative (2 × 1 + 6
 22) ou écrire 2 × 1 + 6
≠ 22.
22) ou écrire 2 × 1 + 6
≠ 22.
Résolution d’équations par inspection
Selon cette stratégie, les élèves reconnaissent la relation d’égalité que représente l’équation. Elles et ils comparent les quantités et font appel à leur sens du nombre pour déterminer la valeur de la variable. Voici trois exemples de la résolution de l’équation c + 45 = 98 par inspection.
Exemple 1
Une ou un élève reconnaît qu’elle ou il doit trouver le nombre qui, additionné à 45, donne une somme de 98. Pour ce faire, il utilise son sens du nombre. Puisqu’il sait que 45 + 45 = 90, il conclut que le nombre qu’il cherche est 8 de plus que 45, soit 53.
Exemple 2
Une ou un élève reconnaît que, si l’on enlève une même quantité de chaque côté de l’égalité, l’équation est modifiée, mais l’égalité est maintenue.
c + 45 = 98
c + 45 – 45 = 98 – 45
c = 98 – 45
c = 53
Note : Il est important que les élèves effectuent ce raisonnement en étapes, sinon elles et ils risquent de simplement appliquer mécaniquement une procédure incomprise. De plus, ce raisonnement peut être utilisé pour mieux saisir le concept d’opération inverse, c’est-à-dire que la soustraction est l’opération inverse de l’addition.
Exemple 3
Une ou un élève décompose un nombre, puis compare ou annule les nombres.
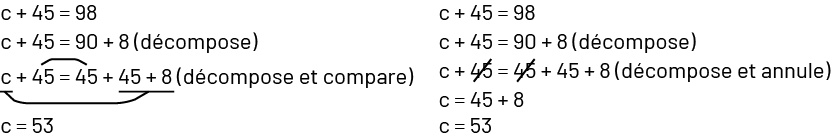
Avantages de la résolution d’équations par inspection :
- Les élèves s’exercent à décoder l’équation, c’est-à-dire à donner un sens au symbolisme de l’équation. Elles et ils développent ainsi leur sens du symbole, de l’équation et de l’égalité.
- Les élèves réfléchissent aux opérations et aux nombres au lieu de chercher à utiliser une procédure vide de sens.
Dans les exemples ci-dessus, on peut reconnaître que les élèves peuvent résoudre une même équation par inspection en utilisant diverses stratégies. Les stratégies comparer des termes, décomposer des termes et modifier l’équation, qui ont été explorées au cours de l’analyse d’une égalité, s’appliquent très bien dans les situations de résolution d’équations par inspection, puisque l’équation représente une égalité. Le personnel enseignant devrait aider les élèves à établir ce lien en faisant ressortir la similitude entre une égalité et une équation à résoudre.
Résolution d’équations par inspection et à l’aide du modèle de la balance
 Description de la vidéo
Description de la vidéo
Description à venir
Résolution d’équations à l’aide d'un logigramme
 Description de la vidéo
Description de la vidéo
Description à venir
Équation qui représente une relation entre deux quantités changeantes
Les élèves apprennent à représenter des relations entre deux quantités en changement au moyen d’équations. Ces équations expriment d’abord une relation entre deux variables, mais on peut profiter de l’occasion pour les convertir en équations à résoudre afin qu’elles et ils substituent des valeurs à une variable dans une équation et déterminer la valeur inconnue.
On peut aussi renforcer les liens entre l’équation et la table de valeurs.
Exemple
Voici une suite de figures :
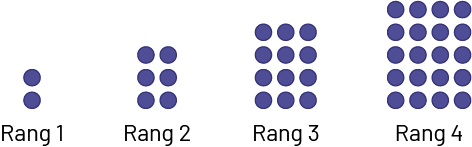
On s’intéresse à la relation entre le rang de la figure et le nombre de points qui la composent.
Certaines et certains élèves pourraient représenter la relation au moyen de l’équation p = r × (r + 1), où r représente le rang de la figure et p, le nombre de points qui la composent. La table de valeurs ci-dessous représente aussi cette relation.
| Rang de la figure (r) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Nombre de points (p) | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | 90 | 110 |
Les élèves peuvent établir des liens entre l’équation et la table de valeurs; par exemple, si r = 1, l’équation devient p = 1 × (1 + 1), d’où p = 2, ce qui correspond aux données dans la table. Si r = 3, l’équation devient p = 3 × (3 + 1), d’où p = 12, ce qui correspond aussi aux données dans la table. Ainsi, la question « Combien de points composent la figure au 9e rang? » peut être exprimée par l’énoncé « Résolvez l’équation p = 9 × (9 + 1). » Pour la résoudre, les élèves peuvent utiliser la table de valeurs en cherchant la valeur de p pour laquelle r = 9 ou effectuer le calcul et déterminer que p = 90.
De même, une question telle que « Quel est le rang qui compte 72 points? » peut être exprimée par l’énoncé « Résolvez l’équation 72 = r × (r + 1). », car, dans l’équation p = r × (r + 1), p prend une valeur de 72. Pour la résoudre, les élèves peuvent chercher, dans la table de valeurs, la valeur de n pour laquelle p = 72 et conclure que r = 8.
Équation qui sert de formule
Dans le domaine Sens de l’espace, les élèves apprennent à exprimer des façons de représenter l’aire et le volume au moyen de formules; par exemple, lorsqu’elles et ils apprennent à déterminer l’aire de rectangles, elles et ils découvrent que la longueur de la base du rectangle (6 cm, par exemple) leur indique le nombre de centimètres carrés qu’elles et ils peuvent placer dans une rangée. La hauteur du rectangle (4 cm, par exemple) indique le nombre de rangées qu’il peut contenir. Donc, le produit de ces nombres (6 × 4 = 24) indique le nombre total de centimètres carrés que peut contenir le rectangle. Elles et ils peuvent généraliser ce résultat au moyen d’une formule, par exemple A = b × h. Ce faisant, les élèves peuvent comprendre le sens d’une formule et des variables qui la composent plutôt que de l’appliquer mécaniquement.
Ces équations (formules) formées de variables peuvent aussi servir à générer des équations à résoudre; par exemple, la question « Quelle est la hauteur d’un rectangle qui a une base de 8 cm et une aire de 72 cm2? » peut être traduite en langage algébrique par « Résolvez l’équation 72 = 8 × h. ».
Équation qui généralise une situation d’égalité
Les élèves peuvent rencontrer ce type d’équation, notamment en explorant les propriétés des nombres et des opérations (m – m = 0, par exemple). Ces équations expriment de façon symbolique le fait qu’une situation d’égalité est toujours vraie, peu importe les valeurs que prennent la ou les variables qui les composent et peu importe qu’il s’agisse de nombres naturels, de fractions ou de nombres décimaux.
Dès le cycle primaire, les élèves explorent certaines propriétés des nombres et des opérations (propriété du 0 dans une addition et commutativité de l’addition, par exemple), puis formulent, à l’aide de mots, des conjectures au sujet de ces propriétés. Au cycle moyen, les élèves poursuivent leur exploration des propriétés et progressent vers la formulation de généralisations à l’aide de mots ou d’une équation. Il importe cependant de noter que l’utilisation d’une équation pour généraliser une situation d’égalité requiert une bonne capacité d’abstraction. Ce n’est qu’après avoir développé une bonne compréhension des propriétés que les élèves sont en mesure de bien saisir le sens de telles équations.
Voici quelques exemples de propriétés des nombres et des opérations, exprimées en mots et à l’aide d’une équation.
| Situation d’égalité | Conjecture en mots | Généralisation à l’aide d’une équation |
|
0 + 2230 = 2230 0 + 9,72 = 9,72 |
« Lorsqu’on ajoute un nombre quelconque à 0, on obtient ce nombre. » |
0 + m = m |
|
\(776 - 0 = 776\) \(\frac{3}{4} - 0 = \frac{3}{4}\) |
« Lorsqu’on soustrait 0 d’un nombre quelconque, on obtient ce nombre. » |
m – 0 = m |
|
0 × 15 = 0 \( 0 \times \frac{3}{4} = 0\) |
« Lorsqu’on multiplie 0 par un nombre quelconque, on obtient 0. » |
0 × n = 0 |
|
1 × 235 = 235 1 × 1,56 = 1,56 |
« Lorsqu’on multiplie 1 par un nombre quelconque, on obtient ce nombre. » |
1 × n = n |
|
4 + 3 = 3 + 4 |
« Lorsqu’on additionne deux nombres, l’ordre dans lequel on les additionne n’est pas important. » Note : Au cycle moyen, le personnel enseignant peut amener les élèves à reconnaître que cette propriété s’applique aussi à la somme de plus de deux nombres. |
a + b = b + a |
Le personnel enseignant doit favoriser le cheminement des élèves vers une compréhension des équations qui généralisent une situation d’égalité. L’exemple ci-dessous décrit une démarche en ce sens, qui mène à la généralisation de la propriété de distributivité de la multiplication sur l’addition.
Exemple
À l’aide de matériel concret, montrer aux élèves que, pour calculer 3 × 24, on peut calculer 3 × 20 et 3 × 4 séparément, puis faire la somme des produits.
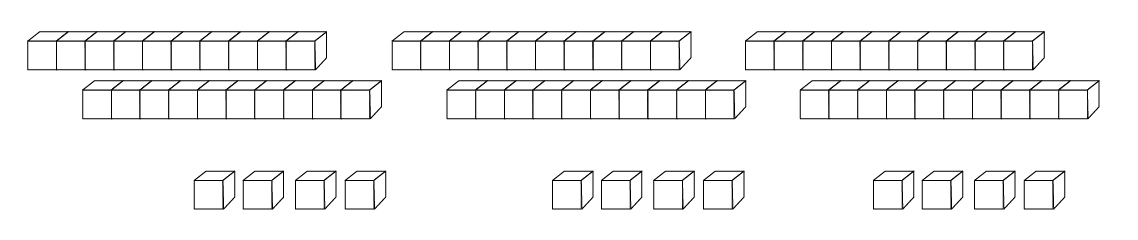
Par la suite, présenter aux élèves diverses égalités se rapportant à la propriété de distributivité de la multiplication sur l’addition.
Exemple
4 × 27 = (4 × 20) + (4 × 7)
11 × 34 = (11 × 30) + (11 × 4)
Pour chacune, demander aux élèves d’expliquer, de représenter et d’analyser la propriété en posant des questions qui favorisent la réflexion telles que :
- L’égalité est-elle vraie? Comment le savez-vous?
- Pouvez-vous le démontrer à l’aide de matériel concret?
- Pouvez-vous vérifier l’égalité sans faire de calcul?
- Est-ce que ça fonctionnerait avec d’autres nombres?
- Pouvez-vous représenter l’égalité à l’aide d’une disposition rectangulaire?
Tout le long de l’exploration, inciter les élèves à formuler des conjectures liées aux égalités présentées, par exemple : « Lorsqu’un nombre est multiplié par un autre nombre, le second nombre peut être décomposé avant d’être multiplié par le premier. »
Présenter ensuite aux élèves des équations qui font appel à la distributivité et qui peuvent être résolues facilement sans effectuer de calcul.
Exemple
7 × 31 = (7 × □) + (7 × 1)
6 × 28 = (□ × 20) + (6 × 8)
7 × 9 = (3 × 9) + (□ × 9)
(20 × 8) + (□ × 8) = 23 × 8
Poser des questions qui mènent les élèves à une généralisation, à savoir que la propriété de distributivité de la multiplication sur l’addition est vraie, peu importe les nombres utilisés. Leur demander de représenter symboliquement cette propriété à l’aide d’une équation; par exemple, a × (b + c) = (a × b) + (a × c).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 89-97.
Connaissance : équation
Relation d’égalité qui comporte une ou plusieurs variables.
Exemple
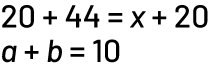
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques, de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : variable
Terme indéterminé (symbole ou lettre) dans une équation, qui peut être remplacé par une ou plusieurs valeurs.
Exemple
Dans l’équation 10 = a + 9, a est une variable, car la valeur est inconnue. On peut la remplacer par une seule valeur, soit par 1, pour rendre l’équation vraie.
Dans l’équation 10 = x + y, les lettres sont des variables, car on peut les remplacer par différentes valeurs.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques, de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
