D1.4 Déterminer le ou les modes de divers ensembles de données présentées dans des diagrammes concrets, des diagrammes à pictogrammes, des lignes de dénombrement, des diagrammes à bandes et des tableaux, et expliquer ce que ces valeurs indiquent au sujet des données.
HABILETÉ : EXPLIQUER CE QUE LE OU LES MODES INDIQUENT AU SUJET DES DONNÉES
Les mesures statistiques sont des nombres utilisés pour caractériser un ensemble de données. Par exemple, le mode est une mesure statistique. Les mesures statistiques sont présentées dans le cadre de la quatrième étape du processus d’enquête, soit l’interprétation des résultats, parce qu’elles constituent une autre façon d’attribuer un sens aux données et qu’elles peuvent fournir des renseignements sur lesquels on peut s’appuyer pour prendre une décision.
Différentes mesures statistiques sont couramment utilisées en Données. Celles qui font l’objet d’étude au cycle primaire sont le mode (à partir de la 2e année) et la moyenne (à partir de la 3e année). Les élèves doivent bien comprendre ce que chacune représente afin de les choisir, de les déterminer et de les utiliser de façon appropriée.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 107.
CONNAISSANCE : MODE
Le mode d’un ensemble de données représente la ou les données ayant la plus grande fréquence, c’est-à-dire la ou les données qui paraissent le plus souvent. Le mode est particulièrement significatif dans des contextes d’enquêtes où on cherche à déterminer ce qui est le plus populaire, le plus vendu, le plus fréquent, etc. Comme en témoignent les exemples ci-dessous, il est possible de déterminer le mode d’un ensemble de données quantitatives ou qualitatives.
Exemple 1
Le tableau ci-dessous présente les données correspondant au nombre d’enfants dans les familles des élèves de la classe. On constate que la donnée la plus fréquente est 2, ce qui indique qu’il y a davantage de familles de deux enfants. Le mode de cet ensemble de données quantitatives est donc de deux enfants par famille.
Nombre d’enfants dans les familles des élèves de la classe
| Nombre d'enfants dans ta famille | Nombre d'élèves |
|---|---|
| 1 | 3 |
| 2 | 12 |
| 3 | 6 |
| 4 | 3 |
| plus de 4 | 2 |
Exemple 2
Le prochain diagramme porte sur les couleurs préférées des élèves de la classe. Pour déterminer le mode de ces données qualitatives, il suffit d’examiner la longueur des bandes. Or, on constate que la bande rouge et la bande bleue sont d’égale longueur et qu’elles sont plus longues que toutes les autres. Dans ce cas, il y a donc deux modes, soit le rouge et le bleu.
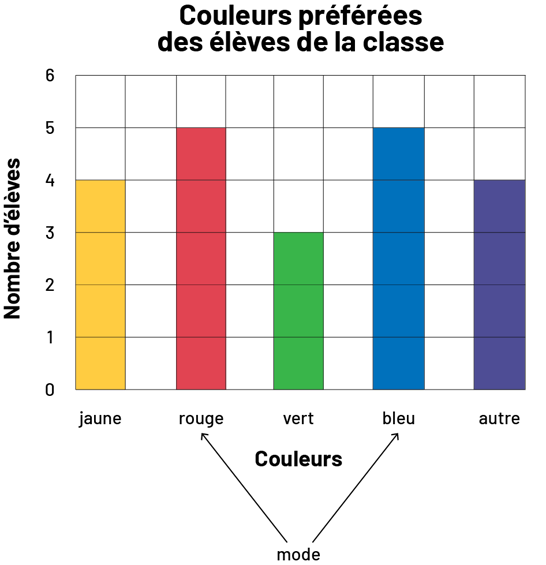
Lorsqu’on utilise le mode pour répondre à une question d’intérêt ou pour prendre une décision, il est important de tenir compte de l’ensemble des données. En effet, dans certaines situations, la donnée la plus fréquente n’est pas nécessairement celle qui donne le meilleur sens aux données. Il est important d’inciter les élèves à examiner chaque situation de près avant de formuler des conclusions fondées sur le mode.
Voici quelques exemples de situations dans lesquelles on évalue la pertinence d’utiliser le mode comme valeur représentative des données :
- Dans l’exemple 1 précédent, le mode de deux enfants par famille semble assez représentatif de la situation puisqu’il y a un écart important entre cette fréquence et les autres.
- Dans l’exemple 2 précédent, non seulement y a-t-il deux modes (le rouge et le bleu), mais l’écart entre leur fréquence et les autres fréquences n’est pas très grand. Il est donc difficile de conclure que ces deux modes représentent une préférence de couleur marquée. Dans ce cas, il serait préférable de mentionner que le rouge et le bleu sont légèrement plus populaires, mais que le jaune suit de près.
- D’après la ligne de dénombrement ci-dessous, le mode correspond à 60 battements de cœur par minute. On constate que ce nombre est éloigné de l’intervalle qui compte la plupart des données (69 à 77). De plus, on voit que l’étendue des données (29) est grande et que les données ne paraissent qu’une, deux ou trois fois chacune. Il serait donc préférable de ne pas utiliser le mode pour formuler une conclusion au sujet de cet ensemble de données.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 108-111.
