D1.3 Choisir le diagramme le plus approprié pour représenter divers ensembles de données à partir d’une variété de diagrammes, y compris des diagrammes à bandes multiples; représenter ces données à l’aide de diagrammes comprenant des sources, des titres, des étiquettes et des échelles appropriés, et justifier son choix.
HABILETÉ : CHOISIR LE DIAGRAMME APPROPRIÉ POUR REPRÉSENTER DIVERS ENSEMBLES DE DONNÉES
Visualisation – La représentation des données au moyen de tableaux et de diagrammes permet de communiquer des renseignements en vue de leur interprétation.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 62.
Une représentation plutôt qu’une autre…
«Il n’existe pas de critères préétablis pour comparer la valeur d’une représentation avec celle d’une autre. La valeur relative d’une représentation dépend de l’intention de la question d'intérêt. Les diagrammes ne sont pas meilleurs que les tableaux, les diagrammes à bandes ne sont pas meilleurs que les diagrammes à pictogrammes, etc. Tout dépend du but de l’élève au moment de créer la représentation.» [traduction libre]
(National Council of Teachers of Mathematics, 2003, p. 199.)
Comment organiser les données
Divers tableaux et diagrammes sont couramment utilisés en traitement des données pour représenter des ensembles de données avec clarté et pour en faciliter l’analyse. Chacun a ses avantages ainsi que ses limites. Il importe toutefois de noter que, en général, la création d’un tableau précède la création d’un diagramme.
Au cycle moyen, selon le contenu d’apprentissage du programme-cadre, les élèves représentent les données à l’aide d’une variété de diagrammes, y compris des diagrammes à bandes multiples, des diagrammes à bandes empilées, des histogrammes et des diagrammes à ligne brisée. Ces dernières sont des représentations symboliques.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 66-67.
HABILETÉ : REPRÉSENTER DES ENSEMBLES DE DONNÉES
La représentation de données dans des tableaux et des diagrammes favorise la communication de renseignements en vue de leur interprétation.
Les élèves doivent déterminer la meilleure façon de regrouper les données recueillies afin de faciliter leur analyse. Par la suite, elles et ils doivent choisir un mode de représentation approprié et le construire de façon à s’assurer de la clarté du message transmis.
Une fois que les données ont été recueillies et enregistrées, les élèves doivent les regrouper à l’intérieur d’un nombre restreint de catégories. Il n’y a pas de règle qui dicte la façon de regrouper les données. Le choix du regroupement dépend en grande partie de la sorte de données recueillies.
Une fois que les données relatives à une enquête ont été regroupées par catégories dans un tableau de fréquences ou autre, il est souvent très utile de les représenter à l’aide d’un diagramme en raison de son impact visuel. En effet, un diagramme :
- présente l’information de façon organisée;
- est généralement plus facile à lire et à interpréter qu’une représentation de données à l’aide d’un texte ou d’un tableau;
- permet de voir l’ensemble des données en un coup d’œil et de s’en faire une première impression (par exemple, si les données sont réparties également ou inégalement entre les catégories);
- facilite la prochaine étape du processus d’enquête, soit l’analyse des données et l’interprétation des résultats.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 81-83.
Par exemple, les élèves peuvent représenter un ensemble de données statistiques de façon beaucoup plus succincte et efficace à l’aide d’un tableau ou d’un diagramme qu’à l’aide d’une description orale. Les élèves doivent cependant apprendre à utiliser correctement les diverses représentations conventionnelles des données (par exemple, tableau de fréquences, diagramme à tiges et à feuilles, diagrammes à bandes multiples) afin de s’assurer que le message transmis est le bon et qu’il est bien compris par les autres. Les élèves peuvent ensuite utiliser ces représentations pour justifier un raisonnement ou appuyer un argument au cours d’un échange mathématique en groupe-classe.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 30.
Les sources, les titres, les étiquettes et les échelles fournissent des précisions importantes sur les données d’un diagramme, notamment:
- la source indique l’origine des données recueillies;
- le titre présente les données du diagramme;
- les étiquettes indiquent les catégories ayant servi au classement des données;
- les échelles indiquent les valeurs sur un axe du diagramme.
L’ordre des catégories est important dans les diagrammes présentant des données quantitatives. Les nombres sont placés en ordre croissant. En revanche, l’ordre des catégories importe peu dans les diagrammes présentant des données qualitatives (par exemple, les couleurs peuvent être placées dans n’importe quel ordre).
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
HABILETÉ : JUSTIFIER SON CHOIX DE DIAGRAMME
Afin de pouvoir bien cibler le meilleur type de représentation de données en fonction de celles recueillies, les élèves doivent comprendre les caractéristiques et les objectifs des différents types de diagrammes. Alors que les données peuvent être visualisées au moyen de différentes représentations, il est important de sélectionner celle qui assure la meilleure clarté et précision des données en contexte. Par exemple, les diagrammes à pictogrammes, les lignes de dénombrement, les diagrammes à bandes et les diagrammes à bandes multiples sont utilisés pour présenter des données qualitatives et des données discrètes.
Les élèves de la 4e année représentent des ensembles de données pour la première fois dans des diagrammes à tiges et à feuilles, et dans des diagrammes à bandes multiples. Toutefois, il importe de rappeler les types de diagrammes vus dans les années précédentes afin que les élèves puissent choisir le diagramme approprié selon les données et ainsi justifier leur choix.
CONNAISSANCE : TYPES DE DIAGRAMME
Ligne de dénombrement
La ligne de dénombrement est utile pour représenter un grand nombre de données numériques. Chaque donnée est représentée par un X et les X correspondant à une même quantité sont disposés l’un au-dessus de l’autre de manière à former des colonnes. Puisque la hauteur de chaque colonne correspond alors à la taille de la donnée qu’elle représente, l’analyse des données s’effectue facilement.
Exemple
L’enseignante ou l’enseignant demande à ses élèves de vérifier depuis combien d’années leurs parents demeurent dans leur logis actuel. Les résultats sont représentés par la ligne de dénombrement suivante.
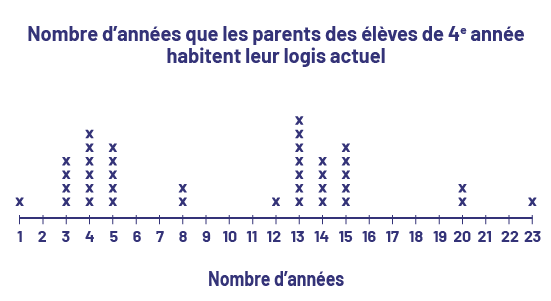Image La
ligne de dénombrement s’intitule : « Nombre d’années que les parents des élèves de quatrième année habitent leur logis
actuel ». La ligne intitulée « Nombre d’années » est graduée de 1 à 23. Le chiffre 1 affiche la présence d’un X. Le
chiffre deux ne présente aucun X. Le chiffre 3 présente 4 X. Le chiffre 4 présente 6 X. Le chiffre 5 présente 5 X. Les
chiffres 6 et 7 ne présentent aucun X. Le chiffre 8 présente deux X. Les nombres 9, dix et 11 ne présentent aucun X.
Le nombre 12 présente un X. Le nombre 13 présente 7 X. Le nombre 14 présente 4 X. Le nombre 15 présente 5 X. Les
nombres 16, 17, 18 et 19 ne présentent aucun X. Le nombre 20 présente deux X. Les nombres 21 et 22 ne présentent aucun
X. Le nombre 23 présente un X.
On voit facilement, d’après la répartition des X, qu’il y a eu deux vagues de déménagements, soit il y a de 3 à 5 ans et de 13 à 15 ans, ce qui pourrait être le résultat de la construction de nouveaux logis ou de la création de nouveaux emplois dans la ville.
Caractéristiques d’une ligne de dénombrement:
- elle a un titre;
- elle a un axe horizontal gradué portant une étiquette;
- chaque donnée est représentée par un X. Les X qui représentent une même donnée numérique sont superposés et sont séparés les uns des autres par un espace constant.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 83-84.
Diagramme à bandes (verticales ou horizontales)
Le diagramme à bandes sert à représenter des données aux fins de comparaison. Il est composé de bandes rectangulaires dont la longueur correspond à la fréquence d’une valeur. Il permet de voir, en un coup d’œil, la distribution des données dans chacune des catégories.
Note : Pour faciliter la création de diagrammes à bandes, il est recommandé de demander aux élèves d’utiliser du papier quadrillé.
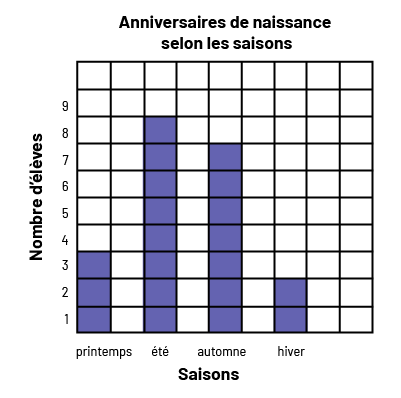
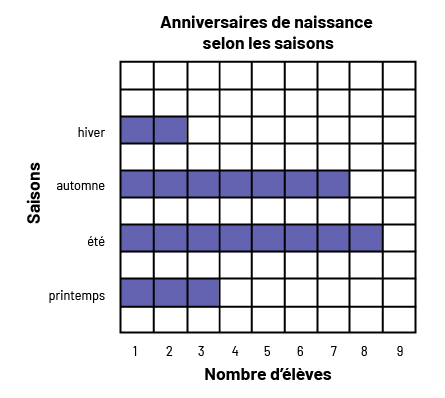Image Un
diagramme à 4 bandes violettes horizontales s’intitule « Anniversaires de naissance selon les saisons ». L’axe
horizontal est nommé « Nombre d’élèves », et l’axe vertical est nommé « Saisons ». Au printemps, la bande indique
trois élèves. À l’été, la bande indique 8 élèves. À l’automne, la bande indique 7 élèves. Et à l’hiver, la bande
indique deux élèves. Caractéristiques d’un diagramme à bandes
- Il a un titre (par exemple, Anniversaires de naissance selon les saisons).
- Il a un axe (vertical ou horizontal) gradué selon une échelle appropriée.
- Il a un autre axe qui représente des catégories (par exemple, printemps, été, automne, hiver).
- Les deux axes ont chacun une étiquette (par exemple, Nombre d’élèves, Saisons).
- Les bandes ont la même largeur et leur longueur correspond, en fonction de l’échelle retenue, à la taille de la fréquence qu’elles représentent (par exemple, si l’échelle est par intervalles de 1, une bande de longueur 3 représente une fréquence de 3).
- Les bandes sont séparées par des espaces égaux.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 71-72.
CONNAISSANCE : DIAGRAMME À BANDES MULTIPLES
Le diagramme à bandes multiples ressemble au diagramme à bandes, mais il sert à comparer les données de plusieurs populations pour une même caractéristique. Ces données peuvent provenir de n’importe quel type d’enquête, soit :
- une enquête au moyen d’observations (par exemple, on veut comparer la taille de la police de caractères utilisée dans les divers types de livres placés dans les centres de lecture de 2e année, de 3e année et de 4e année);
- une enquête au moyen d’une expérience (par exemple, on veut comparer la relation qui existe entre le nombre d’heures d’ensoleillement, la quantité d’eau et la croissance de quatre types différents de plants de tomates);
- une enquête au moyen d’un sondage (par exemple, on veut comparer les sports préférés des élèves de la classe 4A, des élèves de la classe 4B et des élèves de la classe 4C);
- une enquête au moyen d’un prélèvement de mesures (par exemple, on veut comparer la longueur des pieds et des mains des enfants ayant 6 ans, 7 ans, 8 ans et 9 ans);
- une enquête au moyen d’une recherche de données existantes (par exemple, on veut comparer les préférences des élèves de la classe quant aux matières scolaires avec celles de l’ensemble des élèves de l’école et des élèves du primaire au Canada).
Puisque les élèves connaissent la façon de créer un diagramme à bandes, il est relativement facile pour l’enseignante ou l’enseignant de les amener à créer un diagramme à bandes multiples. Elle ou il peut, par exemple, leur présenter trois tableaux de fréquences comme les tableaux suivants.
Sports préférés des élèves de la classe 4A
| Sports | Nombre d'élèves |
|---|---|
| Hockey | 9 |
| Basket-ball | 3 |
| Soccer | 3 |
| Autres | 5 |
Sports préférés des élèves de la classe 4B
| Sports | Nombre d'élèves |
|---|---|
| Hockey | 5 |
| Basket-ball | 5 |
| Soccer | 7 |
| Autres | 3 |
Sports préférés des élèves de la classe 4C
| Sports | Nombre d'élèves |
|---|---|
| Hockey | 6 |
| Basket-ball | 4 |
| Soccer | 8 |
| Autres | 2 |
L’enseignante ou l’enseignant demande ensuite aux élèves de créer un diagramme à bandes horizontales pour représenter les sports préférés des élèves de la classe 4A (Figure 1) et deux autres, de couleur différente, pour représenter les sports préférés des élèves de la classe 4B (Figure 2) et 4C (Figure 3).
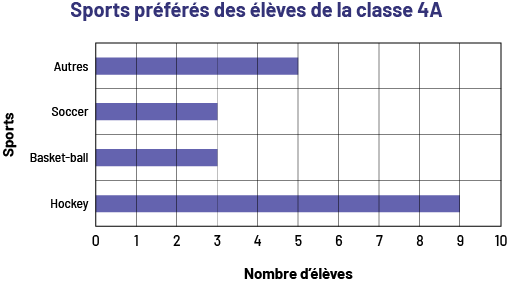Image Un
diagramme à 4 bandes violettes horizontales s’intitule : « Sports préférés des élèves de la classe 4 A ». L’axe
horizontal se nomme « Nombre d’élèves » tandis que l’axe vertical se nomme « Sports ». La bande nommée Hockey atteint
le chiffre 9. La bande nommée Basket-ball atteint le chiffre 3. La bande nommée Soccer atteint le chiffre 3. Et la
bande nommée Autres atteint le chiffre 5. 
Image Un diagramme à 4 bandes rouges horizontales s’intitule : « Sports
préférés des élèves de la
classe 4 B ». L’axe horizontal se nomme « Nombre d’élèves » tandis que l’axe vertical se nomme « Sports ». La bande
nommée Hockey atteint le chiffre 5. La bande nommée Basket-ball atteint le chiffre 5. La bande nommée Soccer atteint
le chiffre 7. Et la bande nommée Autres atteint le chiffre 3 
Image Un
diagramme à 4 bandes noires horizontales s’intitule : « Sports préférés des élèves de la
classe 4 C ». L’axe horizontal se nomme « Nombre d’élèves » tandis que l’axe vertical se nomme « Sports ». La bande
nommée Hockey atteint le chiffre 6. La bande nommée Basket-ball atteint le chiffre 4. La bande nommée Soccer atteint
le chiffre 8. Et la bande nommée Autres atteint le chiffre deux.
L’enseignante ou l’enseignant peut ensuite leur montrer le diagramme à bandes multiples ci-dessous et leur demander de décrire ses caractéristiques.
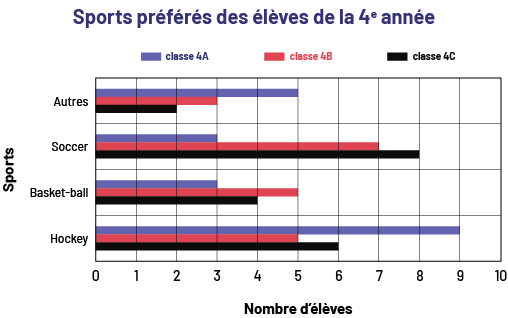Image Un
diagramme à 12 bandes horizontales colorées s’intitule : « Sports préférés des élèves de la quatrième année ». L’axe
horizontal se nomme « Nombre d’élèves » tandis que l’axe vertical se nomme « Sports ». Pour le hockey, la bande
violette pour atteint le chiffre 9, la bande rouge atteint le chiffre cinq et la bande noire atteint le chiffre 6.
Pour le basket-ball, la bande violette atteint le chiffre 3, la bande rouge atteint le chiffre 5 et la bande noire
atteint le chiffre 4. Pour le soccer, la bande violette atteint le chiffre 3, la bande rouge atteint le chiffre 7 et
la bande noire atteint le chiffre 8. Pour les autres sports, la bande violette atteint le chiffre 5, la bande rouge
atteint le chiffre 3 et la bande noire atteint le chiffre deux.
L’enseignante ou l’enseignant présente ensuite aux élèves trois autres tableaux de fréquences, et leur demande de créer un diagramme à bandes multiples qui représente ces données.
Caractéristiques d’un diagramme à bandes multiples
- Il a un titre (par exemple, Sports préférés des élèves de la 4e année).
- Il a un axe gradué selon une échelle appropriée.
- Il a un autre axe qui indique des catégories (par exemple, hockey, basket-ball, soccer, autres).
- Les deux axes ont chacun une étiquette (par exemple, Nombre d’élèves, Sports).
- Pour chaque catégorie, il y a deux bandes contiguës ou plus de couleur différente, chacune représentant un groupe de données (par exemple, les bandes bleues représentent les élèves de la classe 4A contrairement aux bandes rouges et noires qui représentent respectivement les élèves de la classe 4B et 4C).
- Les bandes ont la même largeur et leur longueur correspond, en fonction de l’échelle retenue, à la taille de la fréquence qu’elles représentent (par exemple, si l’échelle est par intervalles de 1, une bande de longueur 3 représente une fréquence de 3).
- Les bandes d’une même catégorie sont séparées des bandes d’une autre catégorie par des espaces égaux.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 75-76.