D1.6 Examiner divers ensembles de données présentées de diverses façons, y compris à l’aide de diagrammes à bandes empilées et de diagrammes trompeurs, en se posant des questions au sujet des données et en y répondant, en remettant en question des idées reçues et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées.
HABILETÉ : EXAMINER ET ANALYSER DES DONNÉES REPRÉSENTÉES DANS DIVERS DIAGRAMMES
L’habileté à interpréter des résultats est liée à l’habileté à raisonner dans la mesure où elle exige une certaine capacité de réflexion et d’analyse. Le personnel enseignant doit aider les élèves à développer cette habileté en leur proposant diverses activités qui portent sur l’interprétation des résultats et en leur posant des questions qui les incitent à examiner ces résultats de près. Ce faisant, il contribuera aussi au développement chez les élèves de compétences en matière de littératie statistique.
Gal (2002, p. 1 à 25) suggère que l’interprétation des résultats doit se faire selon deux points de vue, soit celui de l’enquêtrice ou de l’enquêteur et celui de la lectrice ou du lecteur. Du point de vue de l’enquêtrice ou de l’enquêteur, les élèves examinent des données qu’elles et ils ont recueillies dans le cadre d’une enquête et qu’elles et ils ont résumées dans des diagrammes ou des tableaux. Elles et ils les interprètent ensuite en vue de répondre à la question d’intérêt qu’elles et ils ont posée au début de l’enquête. Du point de vue de la lectrice ou du lecteur, les élèves examinent des données qui proviennent de l’extérieur, c’est-à-dire qui ont été collectées par d’autres. Dans ce contexte, le personnel enseignant peut en profiter pour leur présenter des données qui sont liées à d’autres matières, comme sciences et technologie, études sociales, éducation physique et santé.
Lorsque le personnel enseignant présente un tableau ou un diagramme aux élèves, il s’assure de leur accorder suffisamment de temps de réflexion pour qu’elles et ils puissent en examiner les données et s’en faire une idée générale. La réflexion peut se faire individuellement ou en petits groupes. Le personnel enseignant devrait ensuite poser aux élèves des questions ouvertes pour les aider à traduire leurs observations et leurs idées dans leurs propres mots et à élaborer des idées à partir de celles des autres élèves du groupe-classe. Il pourrait, par exemple, leur demander :
- Que remarquez-vous au sujet de ce diagramme?
- Qu’est-ce que ce diagramme présente d’intéressant?
- Que pouvez-vous dire au sujet de ces données?
- Que pouvez-vous dire au sujet de ce diagramme?
Ces questions ouvertes suscitent une diversité de réponses, ce qui permet ainsi aux élèves de communiquer leurs observations, leurs descriptions et leurs conclusions de façon générale. Par la suite, le personnel enseignant peut poser aux élèves des questions plus précises afin de les aider à développer leur habileté à attribuer un sens aux données. En traitement des données, cette habileté comprend trois niveaux de compréhension, soit la lecture des données, l’établissement de liens entre les données et la lecture au-delà des données.
|
Niveau de compréhension |
Description |
|
Lecture des données |
Cerner les données telles qu’elles sont représentées dans le tableau ou le diagramme. |
|
Établissement de liens entre les données |
Comparer certaines données et les combiner afin d’établir des relations entre elles. |
|
Lecture au-delà des données |
Inférer ou prédire des renseignements implicites ou explicites tirés d’un diagramme ou d’un tableau et émettre des conclusions. |
Le personnel enseignant a parfois tendance à s’attarder surtout au premier niveau de compréhension. Or, selon Friel et ses collaborateurs (2001, p. 124 à158), il devrait toujours poser des questions relatives à chacun des trois niveaux, et ce, quelles que soient la représentation ou l’organisation des données. C’est de cette façon que les élèves peuvent acquérir une autonomie dans l’interprétation des diagrammes et des tableaux, ainsi que dans l’utilisation des mesures statistiques.
Dans ce qui suit, une explication plus détaillée de chacun des trois niveaux de compréhension est présentée, ainsi que des exemples de questions pertinentes que le personnel enseignant pourrait poser au cours d’une activité d’interprétation des résultats.
Lecture des données
Au premier niveau de compréhension, les élèves sont en mesure d’identifier :
- les composantes de la représentation; par exemple, le titre du tableau ou du diagramme, l’échelle ou la légende, la désignation des axes, le choix des catégories;
- la valeur de certaines données représentées.
Exemples de questions pertinentes :
- De quoi est-il question dans ce diagramme? (Le titre)
- Combien de … dans la catégorie? Comment le sait-on?
- Combien y a-t-il de catégories?
- Quelle est l’échelle sur l’axe horizontal?
- Que représente l’axe vertical dans ce diagramme?
- Que représente la plus grande bande?
Établissement de liens entre les données
Ce deuxième niveau de compréhension demande de considérer les données moins comme « … un amalgame de données personnelles ayant chacune ses propres caractéristiques », que comme « … un ensemble de données collectives avec de nouvelles propriétés » (Konold et Higgins, 2003, p. 202). Ce niveau de compréhension est plus difficile à atteindre, car les élèves doivent analyser les données individuelles en les combinant ou en comparant des ensembles de données.
Au deuxième niveau de compréhension, les élèves sont en mesure :
- de comparer des données en employant des expressions, comme plus que, moins que, autant que, le plus, le moins, un peu plus, trois fois moins, il y a une petite différence entre;
- de comparer les longueurs de bandes dans un diagramme à bandes;
- de faire les liens entre différentes façons de décrire une relation entre des données;
- de combiner certaines données selon certaines catégories et de comparer les fréquences de chacune;
- de décrire certains avantages et désavantages de deux représentations différentes des mêmes données;
- de déterminer la valeur de certaines mesures statistiques (mode, médiane, moyenne) d’un ensemble de données.
Exemples de questions pertinentes :
- Quelle est la catégorie la plus populaire chez les élèves de la 4e, 5e et 6e année?
- Est-ce que le nombre d’élèves possédant ... est plus élevé que le nombre total d’élèves qui possèdent ... ?
- Parmi les métaux produits au Canada en 2004, y en a-t-il dont plus de la moitié de la production provient de l’Ontario?
- De combien de plus de … y a-t-il comparativement à … ?
- Y a-t-il une catégorie qui surpasse, à elle seule, toutes les autres en termes de fréquence?
- Pourquoi a-t-on présenté ces données dans deux diagrammes plutôt qu’un?
Lecture au-delà des données
Bien que la lecture explicite et littérale de données représentées dans un diagramme ou un tableau soit une composante importante de l’habileté à lire des diagrammes, la lectrice ou le lecteur exploite le plein potentiel du diagramme lorsqu’elle ou il est capable d’interpréter et de généraliser en utilisant ces données (Kirk et coll., 1980, p. 382, traduction libre).
Au troisième niveau de compréhension, les élèves font appel à plusieurs habiletés de la pensée critique et statistique. Elles et ils sont en mesure :
- de reconnaître ce que le diagramme ou le tableau ne « dit pas » directement;
- de préciser la tendance d’un ensemble de données;
- de faire des inférences et des prédictions;
- de tirer des conclusions et de les justifier;
- d’évaluer la crédibilité et la logique des prédictions et des conclusions;
- d’évaluer la représentativité de l’étendue, du mode, de la médiane et de la moyenne;
- de faire un retour sur les étapes du processus d’enquête.
Questions pertinentes
- Pensez-vous que … est le plus commun dans toutes les villes? Pourquoi?
- Si l’on refait le sondage en utilisant d’autres choix de réponse, les résultats seront-ils semblables?
- Comment pourrait-on organiser les données pour découvrir d’autres renseignements? (Par exemple, en regroupant les données des élèves du cycle primaire et celles des élèves du cycle moyen, on peut analyser la préférence des élèves en général.)
- Quelles autres questions peut-on poser à l’aide du diagramme?
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 89-97.
HABILETÉ : À PARTIR D’UN DIAGRAMME, TIRER DES CONCLUSIONS, FORMULER DES ARGUMENTS ET PRENDRE DES DÉCISIONS
Après avoir examiné et analysé les données (trois niveaux de compréhension, soit la lecture des données, l’établissement de liens entre les données et la lecture au-delà des données) d’un diagramme, les élèves sont amenées et amenés à tirer des conclusions, à formuler des arguments et à prendre des décisions.
L’interprétation des résultats permet de tirer des conclusions pertinentes pour répondre à des questions d’intérêt et prendre des décisions réfléchies.
L’étude de la statistique comprend la collecte, l’organisation, la représentation, l’analyse et l’interprétation de données. Ces données sont ensuite utilisées pour prédire, faire des inférences et prendre des décisions. […] Les élèves ont besoin de développer les habiletés qui leur permettront de vivre dans une société où les statistiques sont omniprésentes, sans être induites et induits en erreur. Sans ces habiletés, leurs connaissances pour comprendre le monde seront insuffisantes (Burns, 2000, p. 59, traduction libre).
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 89.
La prise de décision est très importante dans le processus d’enquête, puisque sans prise de décision, le processus perd tout son sens. En effet, pourquoi mettre sur pied une enquête afin de recueillir, d’organiser et d’analyser des données si l’on n’a pas l’intention d’en tirer des conclusions? Dans plusieurs cas, la prise de décision se limite à donner une réponse à la question que l’on se posait initialement. Dans d’autres cas, il s’agit d’utiliser cette réponse pour décider si l’on doit agir dans tel ou tel sens. Le personnel enseignant doit donc amener les élèves à répondre à la question d’intérêt qui est à l’origine de l’enquête ou à prendre une décision en se basant sur :
- les relations établies entre les données;
- le sens qu’elles et ils ont dégagé des données;
- les conclusions qu’elles et ils en ont tiré.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 101.
CONNAISSANCE : DIAGRAMME TROMPEUR
Un diagramme est une représentation schématique d’un ensemble de données. Il y a différents types de diagrammes, comme le diagramme de Venn, le diagramme à bandes, le diagramme à bandes multiples et le diagramme à bandes empilées.
Note : Un diagramme peut refléter un biais s’il n’est pas bien construit.
Exemple
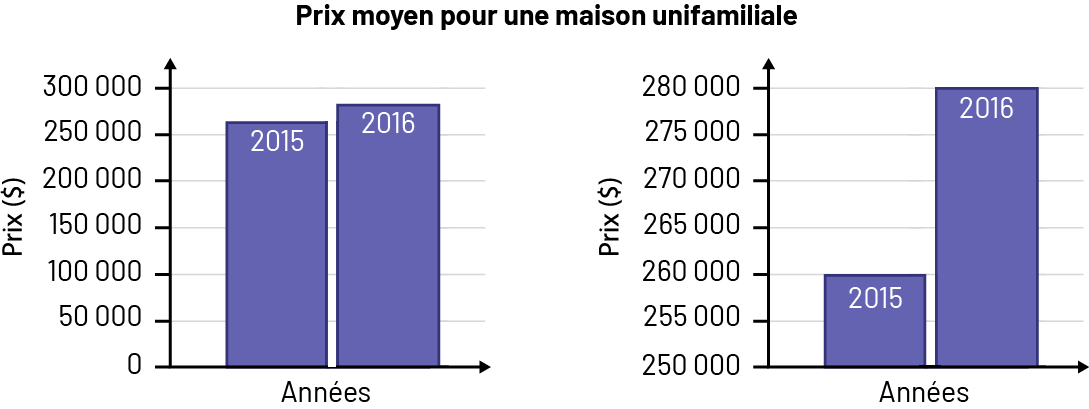 image Le
titre des deux diagrammes à bandes est : Prix moyen pour une maison unifamiliale.Dans le premier graphique, le titre
de l’axe des x est « Années ». Sur la première bande, il est écrit 2015, sur la seconde bande, il est écrit 2016. Les
deux bandes ont presque la même hauteur.Le titre de l’axe des y est « Prix (en dollars) ». L’axe est gradué par
50 000, soit de 0 à 300 000.Dans le second graphique, le titre de l’axe des x est « Années ». Sur la première bande,
il est écrit 2015, sur la seconde bande, il est écrit 2016. La bande 2015 est plus beaucoup petite que la bande
2016.Le titre de l’axe des y est « Prix (en dollars) ». L’axe est gradué par 5 000, soit de 250 000 à 280 000.
image Le
titre des deux diagrammes à bandes est : Prix moyen pour une maison unifamiliale.Dans le premier graphique, le titre
de l’axe des x est « Années ». Sur la première bande, il est écrit 2015, sur la seconde bande, il est écrit 2016. Les
deux bandes ont presque la même hauteur.Le titre de l’axe des y est « Prix (en dollars) ». L’axe est gradué par
50 000, soit de 0 à 300 000.Dans le second graphique, le titre de l’axe des x est « Années ». Sur la première bande,
il est écrit 2015, sur la seconde bande, il est écrit 2016. La bande 2015 est plus beaucoup petite que la bande
2016.Le titre de l’axe des y est « Prix (en dollars) ». L’axe est gradué par 5 000, soit de 250 000 à 280 000.
Le prix d'une maison a augmenté de 20 000 $ en 1 an. Le premier diagramme montre bien la faible augmentation du prix d'une maison en 1 an (entre 2015 et 2016), puisque l'écart entre les bandes est minime. Le second diagramme est trompeur. Il laisse penser que l'augmentation du prix d'une maison a triplé en 1 an (entre 2015 et 2016), car l'écart entre les bandes est plus grand à cause du choix de l'échelle de l’axe vertical.
Source : En avant, les maths!, 7e année, CM, Données, p. 2.
