D2.2 Déterminer et comparer les probabilités théoriques et expérimentales qu’un événement se produise.
HABILETÉ : COMPARER DES PROBABILITÉS
Raisonnement proportionnel
Il y a un lien important entre la pensée probabiliste et le raisonnement proportionnel. Le raisonnement proportionnel permet de reconnaître la relation d’équivalence entre deux situations de probabilité, ce qui contribue à la compréhension du concept de probabilité théorique. Le personnel enseignant doit proposer aux élèves diverses activités qui les incitent à établir ce lien.
Exemple
Le personnel enseignant présente aux élèves deux sacs et leur contenu. Le sac A contient 3 cubes verts et 2 cubes mauves. Le sac B contient 6 cubes verts et 4 cubes mauves. Il leur pose la question suivante : « Selon vous, dans quel sac a-t-on une plus grande probabilité de prendre au hasard un cube vert? »
Une ou un élève répond : « Je crois que c’est dans le sac B, parce qu’il y a plus de cubes verts. Il y a donc plus de possibilités d’en prendre un au hasard. » Cette réflexion est typique d’une apprenante ou d’un apprenant qui n’a pas encore acquis un raisonnement proportionnel dans un contexte de probabilité. Elle ou il n’a pas compris que les deux situations sont équivalentes, puisque le nombre de cubes verts et le nombre de cubes mauves ont été doublés.
Une ou un autre élève dit : « La probabilité de prendre au hasard un cube vert dans le sac A est de \(\frac{3}{5}\),
alors qu’avec le sac B la probabilité est de \(\frac{6}{10}\); puisque \(\frac{3}{5} = \frac{6}{10}\), la probabilité
est donc la même pour chaque sac. »
Cette réponse montre l’application du raisonnement proportionnel dans un
contexte de fractions équivalentes.
Enfin, une ou un autre élève réorganise les cubes et conclut :
« Dans le sac A, je vois 3 cubes verts sur un total de 5 cubes, alors que, dans le sac B, je vois 3 groupes de cubes verts sur un total de 5 groupes. Je juge qu’il est aussi probable de prendre au hasard un cube vert dans le sac A que dans le sac B. » La réorganisation des cubes est une façon concrète de représenter la relation de proportionnalité.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 144-145.
CONNAISSANCE : PROBABILITÉ THÉORIQUE
L’analyse de données recueillies lors d’expériences aléatoires permet de mieux comprendre le concept de probabilité théorique.
« L’incertitude est omniprésente, et la probabilité sert à quantifier cette incertitude dans les médias et dans les conversations quotidiennes » (Albert, 2006, p. 417, traduction libre).
La probabilité théorique permet de quantifier le caractère aléatoire et incertain d’un événement ou d’un résultat. Cette quantité peut être représentée à l’aide d’une fraction entre 0 et 1. Au jeu de pile ou face, par exemple, la probabilité théorique d’obtenir le résultat « pile » est égale à \(\frac{1}{2}\). Cette fraction indique que le jeu comporte deux résultats équiprobables et qu’un de ces résultats est « pile ». Autrement dit, à ce jeu, on a une possibilité sur deux d’obtenir le résultat « pile ».
Le personnel enseignant doit savoir que si tous les résultats possibles d’une expérience sont équiprobables, la probabilité théorique d’un résultat A quelconque est définie, de façon formelle, comme suit.

Ainsi, si l’on cherche à déterminer la probabilité d’obtenir un nombre pair en lançant un dé à six faces, il suffit de reconnaître qu’il y a six résultats possibles (1, 2, 3, 4, 5 et 6) et que trois de ces résultats correspondent à un nombre pair (2, 4 et 6). On peut donc dire que la probabilité théorique d’obtenir un nombre pair est égale à \(\frac{3}{6}\), c’est-à-dire qu’il y a trois possibilités sur six que le résultat corresponde à un nombre pair. La notation P(A) est couramment employée pour décrire la probabilité d’un résultat A quelconque. Ainsi, dans la situation précédente, on pourrait écrire P(nombre pair) = \(\frac{3}{6}\). Soulignons, cependant, qu’au cycle moyen il est préférable d’aider les élèves à développer une compréhension du concept de probabilité théorique sans trop mettre l’accent sur la définition ou sur la notation formelle. Les stratégies présentées dans ce qui suit vont dans ce sens.
Dans certaines situations, on se rend compte qu’un résultat souhaité ne peut jamais se produire (par exemple, obtenir un nombre supérieur à six en lançant un dé). On dit alors que la probabilité de ce résultat est égale à 0. Dans d’autres situations, il est certain que le résultat souhaité va se produire (par exemple, obtenir un nombre inférieur à 7 en lançant un dé). On dit alors que la probabilité de ce résultat est égale à 1.
La probabilité théorique aide à prendre des décisions réfléchies dans toute situation aléatoire. Puisque dans de telles situations, il est impossible de prédire le résultat sans risquer de se tromper, on peut diminuer ce risque en déterminant la probabilité théorique de chaque résultat et en choisissant le résultat dont la probabilité est la plus élevée. C’est en quelque sorte une façon de « mathématiser le hasard ».
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la
6e année, p. 137-138.
Exemple
Le personnel enseignant présente aux élèves la roulette ci-dessous et leur demande de déterminer la probabilité que l’aiguille s’arrête dans le secteur jaune.
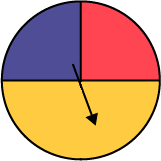 image Une roulette
munie d’une aiguille est séparée en trois parties colorées : la partie jaune prend la moitié de l’espace, tandis que
la partie rouge et la partie violette prennent chacune un quart. L’aiguille pointe dans la partie jaune.
image Une roulette
munie d’une aiguille est séparée en trois parties colorées : la partie jaune prend la moitié de l’espace, tandis que
la partie rouge et la partie violette prennent chacune un quart. L’aiguille pointe dans la partie jaune.
Cette situation peut provoquer un déséquilibre cognitif chez certaines et certains élèves. Intuitivement, elles et ils savent qu’il est plus probable que l’aiguille s’arrête dans le secteur jaune que dans le secteur rouge ou dans le secteur bleu. Cependant, elles et ils se disent qu’il n’y a que trois résultats possibles (secteur jaune, secteur bleu et secteur rouge) et, donc, que la probabilité que l’aiguille s’arrête dans le secteur jaune devrait être égale à \(\frac{1}{3}\). Bien entendu, la faille dans ce raisonnement vient du fait que les trois résultats ne sont pas équiprobables, puisque l’aire du secteur jaune est supérieure à l’aire de chacun des deux autres secteurs. Le personnel enseignant peut alors suggérer aux élèves de diviser le secteur jaune comme suit.
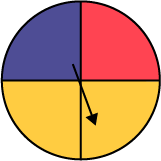 image Une roulette
munie d’une aiguille est séparée en trois parties colorées : la partie jaune prend la moitié de l’espace, tandis que
la partie rouge et la partie violette prennent chacune un quart. L’aiguille pointe dans la partie jaune.
image Une roulette
munie d’une aiguille est séparée en trois parties colorées : la partie jaune prend la moitié de l’espace, tandis que
la partie rouge et la partie violette prennent chacune un quart. L’aiguille pointe dans la partie jaune.
On peut maintenant considérer qu’il y a quatre résultats possibles (jaune, jaune, bleu et rouge) et qu’ils sont équiprobables, puisque l’aire de chaque secteur est la même. La probabilité que l’aiguille s’arrête dans le secteur bleu est de \(\frac{1}{4}\). Il en est de même pour la probabilité qu’elle s’arrête dans le secteur rouge. Cependant, la probabilité que l’aiguille s’arrête dans le secteur jaune est égale à \(\frac{2}{4}\). Il est donc deux fois plus probable que l’aiguille s’arrête dans le secteur jaune que dans le secteur bleu ou le secteur rouge.
Les autres exemples liés au matériel de manipulation n’offrent pas aussi facilement la possibilité de faire ressortir l’idée d’équiprobabilité des résultats. Lorsqu’on utilise un dé ou une pièce de monnaie, on tient pour acquis que les résultats sont équiprobables, c’est-à-dire que l’on suppose que le dé n’est pas pipé ou que la pièce peut naturellement tomber aussi souvent d’un côté que de l’autre. Dans le cas du sac de billes, on suppose qu’au toucher il n’est pas possible de distinguer une bille de l’autre, comme ce serait le cas si, par exemple, la bille rouge était plus grosse que toutes les autres. C’est pourquoi, lorsque les élèves utilisent ce matériel, le personnel enseignant devrait les inciter à toujours établir la prémisse que les résultats sont équiprobables.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 140-141.
La probabilité théorique est un concept mathématique abstrait qui n’est pas toujours facile à saisir. Cependant, sa compréhension est essentielle au développement de la pensée probabiliste. Afin que cette compréhension ne se résume pas à l’apprentissage d’une formule, elle doit être le fruit d’un long processus au cours duquel le personnel enseignant expose les élèves à diverses situations ou expériences ou à divers jeux de probabilité qui leur permettent de confronter la théorie et la pratique. Cette approche crée souvent un déséquilibre chez celles et ceux qui, devant une situation particulière, se laissent mener par leur intuition ou par une analyse fautive. Même chez les adultes, il est très fréquent de mal analyser une situation aléatoire d’apparence simple. Au cycle moyen, il est donc très important de s’en tenir à des situations relativement simples qui font appel à du matériel concret. Dans ce qui suit, on décrit la façon dont le personnel enseignant peut aider les élèves à développer une compréhension du concept de probabilité théorique.
Développement du concept de probabilité théorique
Pour acquérir une bonne compréhension du concept de probabilité théorique, les élèves doivent recourir à la fois à leur pensée intuitive et à leur pensée analytique. Il est donc important que le personnel enseignant leur présente des situations qui font appel à la théorie et à la pratique afin de favoriser un va-et-vient entre ces deux modes de pensée.
Dès leur jeune âge, les élèves acquièrent une compréhension informelle du concept de probabilité. L’utilisation d’un dé, par exemple, dans le contexte de divers jeux leur permet de reconnaître qu’il y a six résultats possibles. Puis, à la longue, elles et ils comprennent intuitivement que, même si ces résultats sont aléatoires, ils sont aussi équiprobables. Au cycle moyen, les élèves acquièrent graduellement une compréhension du concept de probabilité théorique. En 4e année, par exemple, elles et ils peuvent affirmer qu’il y a une possibilité sur six d’obtenir le nombre quatre en lançant un dé. En 5e année, elles et ils apprennent à exprimer cette probabilité à l’aide d’une fraction, soit \(\frac{1}{6}\). En 6e année, elles et ils peuvent aussi utiliser un nombre décimal ou un pourcentage pour représenter la probabilité d’un résultat.
Matériel de manipulation
Pour aider les élèves à développer une compréhension du concept de probabilité théorique, le personnel enseignant doit utiliser du matériel de manipulation varié qui permet de visualiser facilement les différents résultats possibles. Le tableau ci-dessous en présente quelques exemples.
| Matériel | Probabilité théorique |
|---|---|
|
Sac de billes ou de jetons 
|
Si on tire au hasard une bille d'un sac comme celui illustré ci-contre, il y a 5 possibilités en ce qui a trait à la couleur de cette bille. Puisqu'il y a une seule bille de chaque couleur, la probabilité d'obtenir, par exemple, une bille verte est égale à \(\frac{1}{5}\). |
|
Dé 
|
Lorsqu'on lance un dé à 6 faces, les résultats 1, 2, 3, 4, 5, 6 sont équiprobables. Donc, la probabilité d'obtenir le nombre 6 est de \(\frac{1}{6}\). D'autres modèles de dés peuvent aussi êtres utilisés. 
|
|
Roulette 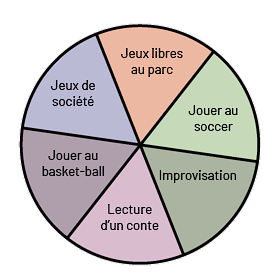
|
Sur la roulette illustrée ci-contre, il y a 6 secteurs de même aire. Donc, la probabilité que l'aiguille s'arrête dans le secteur Jouer au soccer est égale à \(\frac{1}{6}\). |
|
Pièce de monnaie 
|
Lorsqu'on lance une pièce de monnaie, les résultats côté pile et côté face sont équiprobables. Donc, la probabilité d'obtenir le côté pile est de \(\frac{1}{2}\). |
|
Jeton bicolore 
|
Lorsqu'on lance un jeton bicolore comme illustré ci-contre, les résultats côté rouge et côté bleu sont équiprobables. Donc, la probabilité d'obtenir le côté rouge du jeton est égale à \(\frac{1}{2}\). |
Résultats équiprobables
Tout ce matériel aide les élèves à développer une compréhension du concept de probabilité théorique qui est fondée à la fois sur l’intuition et sur la raison, puisque, dans chaque cas, les résultats possibles sont facilement observables et leur nombre est limité. Le modèle de la roulette permet toutefois de faire ressortir, plus que les autres modèles, l’importance de s’assurer que tous les résultats possibles sont réellement équiprobables.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 138-140.
Autres situations
Au fur et à mesure que les élèves acquièrent une compréhension du concept de probabilité théorique, dans le cadre de situations simples, le personnel enseignant peut leur présenter des situations qui nécessitent davantage de réflexion. Il peut proposer, par exemple, des situations comprenant deux choix successifs, des situations comprenant une expérience répétée ou des situations qui font appel à une simulation. Le personnel enseignant peut aussi profiter de ces situations pour faire ressortir certaines erreurs ou méprises communes en probabilité.
Dans chaque cas, il importe toutefois d’y aller à petits pas, de s’en tenir à des situations relativement simples et de s’assurer que les élèves comprennent bien les notions de probabilité qu’elles soutiennent. Sinon, les élèves risquent de construire des méprises qu’elles et ils auront de la difficulté à déconstruire.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 145.
CONNAISSANCE : PROBABILITÉ EXPÉRIMENTALE
Expérience de probabilité
Les expériences de probabilité sont essentielles au développement d’une bonne compréhension du concept de probabilité théorique. Ainsi, lorsque les élèves ont établi la probabilité théorique d’un résultat quelconque, le personnel enseignant peut leur proposer de vérifier cette probabilité de façon expérimentale. Cette activité aide les élèves à mieux comprendre que l’incertitude est inhérente à toute situation liée au hasard; par exemple, même si elles et ils établissent que la probabilité théorique d’un résultat quelconque est égale à \(\frac{1}{4}\), rien ne garantit qu’elles et ils obtiendront ce résultat le quart des fois au cours d’une expérience.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 142.
Les expériences de probabilité permettent d’appuyer ou de remettre en question un raisonnement intuitif; elles sont au cœur du développement de la pensée probabiliste.
Probabilité expérimentale
La probabilité expérimentale est utilisée dans des situations où il est impossible de déterminer la probabilité théorique d’un événement ou d’un résultat en particulier. C’est le cas, par exemple, des prévisions météorologiques, de l’évaluation de l’espérance de vie ou de la probabilité de réussir un lancer franc au basketball. Selon le programme-cadre, c’est en 5e année que les élèves voient le concept de probabilité expérimentale pour la première fois.
L’apprentissage de ce concept devrait se faire dans le cadre de situations concrètes. Le personnel enseignant, par exemple, peut présenter aux élèves diverses situations comportant l’activité de prendre au hasard un objet dans un sac dont le contenu exact est inconnu. Il peut aussi leur présenter des situations où les résultats possibles ne sont pas nécessairement équiprobables.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 150.
Exemple 1
Le personnel enseignant groupe les élèves en équipes de deux. Il leur explique qu’elles et ils doivent effectuer une expérience qui consiste à lancer 20 fois une pièce de monnaie et à noter les résultats. Avant de procéder, les élèves doivent prédire le nombre de fois qu’elles et ils obtiendront chacun des résultats « pile » et « face ». En sachant que la probabilité de chaque résultat est égale à \(\frac{1}{2}\), il se peut que la plupart des élèves prédisent qu’elles et ils obtiendront 10 fois « pile » et 10 fois « face ».
Lorsque les élèves ont terminé l’expérience, le personnel enseignant demande à chaque équipe d’écrire ses résultats dans un tableau.
Expérience de 20 lancers d'une pièce de monnaie
| Équipe | Résultats | P | F | |||
|---|---|---|---|---|---|---|
| 1 | F-P-F-F-P | P-P-F-P-P | P-F-F-P-F | P-F-F-F-F | 9 | 11 |
| 2 | P-P-F-P-P | P-P-P-F-P | F-P-P-P-P | F-P-F-F-F | 13 | 7 |
| 3 | P-P-P-P-P | F-F-F-P-P | P-F-F-F-P | P-F-F-P-F | 11 | 9 |
| 4 | F-F-P-F-P | P-P-P-F-P | P-F-P-P-F | F-P-F-P-F | 11 | 9 |
| 5 | F-F-P-P-P | P-F-F-F-P | P-F-F-P-F | P-F-P-P-F | 10 | 10 |
| 6 | F-P-F-F-P | F-P-F-F-F | P-P-P-F-F | F-P-P-F-P | 9 | 11 |
| 7 | P-P-P-P-F | F-P-P-F-F | P-P-P-F-P | F-F-F-P-P | 12 | 8 |
| 8 | P-P-P-F-F | P-P-P-F-F | F-F-P-F-F | F-P-P-F-P | 10 | 10 |
| 9 | F-P-P-P-P | P-P-P-P-P | P-F-P-F-P | P-P-F-P-P | 16 | 4 |
| 10 | P-F-P-P-P | F-F-P-P-P | F-P-F-P-F | P-F-P-F-P | 12 | 8 |
| Total | 113 | 87 | ||||
Afin d’aider les élèves à mieux comprendre le concept de probabilité théorique, le personnel enseignant les incite à analyser les résultats. Les élèves peuvent souligner que seules les expériences 5 et 8 ont donné 10 fois pile et 10 fois face. Quant aux expériences 1, 3, 4 et 6, elles ont donné des résultats très près de cette distribution. Elles et ils peuvent aussi noter que les résultats de l’expérience 9 (16 fois pile et 4 fois face) sont très différents de ce que la probabilité théorique pourrait laisser croire. Ce résultat permet toutefois de mettre en évidence l’idée que tous les résultats sont possibles, même ceux qui semblent peu probables. Les élèves peuvent aussi constater que sur un total de 200 lancers, le résultat pile a été obtenu 113 fois et le résultat face 87 fois.
Note : Si l’on connaît la probabilité théorique d’un résultat quelconque d’une expérience, la Loi des grands nombres stipule que plus on fait l’expérience un grand nombre de fois, plus le rapport entre la fréquence du résultat et le nombre d’essais se rapprochera de la probabilité théorique. Cette loi n’est pas à l’étude au cycle moyen. Cependant, le personnel enseignant peut profiter des expériences de probabilité pour en présenter l’idée générale aux élèves.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 142-143.
Exemple 2
Le personnel enseignant a une boîte de punaises identiques. Il montre aux élèves que si on lance une punaise en l’air, elle peut tomber en pointant vers le haut ou vers le bas.

Même s’il n’y a que deux résultats possibles, rien ne permet de croire qu’ils sont équiprobables. Il n’est donc pas possible de déterminer la probabilité théorique de chacun. Le personnel enseignant rappelle alors aux élèves qu’à diverses occasions elles et ils ont :
- déterminé la probabilité théorique d’un résultat quelconque;
- réalisé une expérience de probabilité pour en vérifier la vraisemblance;
- constaté qu’avec un nombre assez élevé d’essais le rapport entre la fréquence du résultat recherché et le nombre d’essais était comparable à la probabilité théorique.
Il leur explique que la probabilité expérimentale fait appel à ce constat, c’est-à-dire que si l’on effectue une expérience de probabilité suffisamment de fois et que l’on note la fréquence de chaque résultat, cette fréquence peut être utilisée pour déterminer une approximation de la probabilité théorique.
Le personnel enseignant groupe les élèves en équipes de deux. Il remet une punaise à chaque équipe. Il demande aux élèves d’effectuer 20 lancers, de noter les résultats et de déterminer, à l’aide d’une fraction, ce qui pourrait être la probabilité de chaque résultat. Une équipe, par exemple, obtient les résultats suivants : 12 fois la pointe vers le haut et 8 fois la pointe vers le bas. Les élèves pourraient alors dire que la probabilité que la punaise tombe en pointant vers le haut est d’environ \(\frac{12}{20}\) et que la probabilité qu’elle tombe en pointant vers le bas est d’environ \(\frac{8}{20}\).
Le personnel enseignant anime ensuite un échange mathématique afin de faire ressortir la variabilité des réponses des différentes équipes. Il suggère aux élèves de faire le total des fréquences qu’a obtenues chaque équipe afin d’obtenir une approximation plus fiable de chacune des probabilités.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 150-151.
