D2. Probabilité :
Décrire la probabilité que des événements se produisent et utiliser cette information pour faire des prédictions.
SITUATION D’APPRENTISSAGE : probabilités théoriques et expérimentales d’événements indépendants
Durée totale : environ 120 minutes
Sommaire
Dans cette minileçon, l’élève résout des problèmes de probabilité en comparant des probabilités théoriques avec des probabilités expérimentales d’événements indépendants.
| Attentes | Contenus d'apprentissage |
|---|---|
|
B1. Sens du nombre : Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.3 Comparer et ordonner des nombres entiers, des nombres décimaux et des fractions, séparément et en les combinant, dans divers contextes |
|
B2. Sens des opérations : Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.1 Utiliser les propriétés des opérations et les relations entre les opérations pour résoudre des problèmes comportant des nombres naturels, des nombres décimaux, des fractions, des rapports, des taux, et des pourcentages, y compris des problèmes à plusieurs étapes ou plusieurs opérations |
|
D.2 Probabilité : Décrire la probabilité que des événements se produisent et utiliser cette information pour faire des prédictions. |
D2.2 Déterminer et comparer les probabilités théoriques et expérimentales que deux évènements indépendants se produisent. |
Pistes d’observation
L’élève :
- détermine la probabilité d’un événement en utilisant un diagramme en arbre;
- détermine la probabilité expérimentale d’un événement en réalisant une expérience;
- montre sa compréhension de la relation entre une fraction, un nombre décimal et un pourcentage.
Matériel
- dé
- cartes à jouer
- sac opaque (dans lequel iront les cartes)
- feuille lignée ou blanche
- crayon et efface
- pièce de monnaie
- roulette avec un secteur ombré
Exploration guidée
Déroulement
- Présenter aux élèves l’Exemple 1, soit une situation de probabilité avec un dé dans laquelle l’élève doit trouver et comparer la probabilité théorique et la probabilité expérimentale.
- Allouer aux élèves le temps requis pour effectuer le travail. À cette étape-ci, l’élève découvre diverses stratégies pour trouver la probabilité théorique et la probabilité expérimentale de deux événements indépendants.
- Demander à quelques élèves de faire part au groupe-classe de leur solution et d’expliquer les stratégies utilisées pour trouver la probabilité théorique et ensuite la façon de faire l’expérience et de noter la probabilité. Inviter les autres élèves à poser des questions afin de vérifier leur compréhension.
- À la suite des discussions, s’assurer que les élèves établissent des liens entre la probabilité théorique, la
probabilité expérimentale et la ligne de probabilité.
Note : Au besoin, consulter le corrigé de la partie 1 pour obtenir des exemples de stratégies.
- Encourager les élèves à améliorer leur travail en y ajoutant les éléments manquants.
- Au besoin, présenter aux élèves l’Exemple 2, soit un problème de probabilité avec des cartes à jouer dans lequel l’élève doit premièrement trouver la probabilité théorique et ensuite la probabilité expérimentale en faisant l’expérience.
Exemple 1
Trois amis, Élias, Joyce et Vincent, ont décidé d’inventer un jeu de hasard. Il s’agit de lancer un dé deux fois de suite. La personne gagnante est déterminée de la façon suivante :
- si les deux lancers sont des nombres impairs, Élias obtient un point;
- si les deux lancers sont des multiples de trois, Joyce obtient un point;
- si les deux lancers sont des nombres supérieurs à trois, Vincent obtient un point.
Détermine la probabilité théorique et la probabilité expérimentale de ces événements. Qui a la meilleure chance de gagner à ce jeu de hasard?
Stratégie 1 – Probabilité théorique
Je dénombre les résultats possibles à l’aide d’un diagramme en arbre.
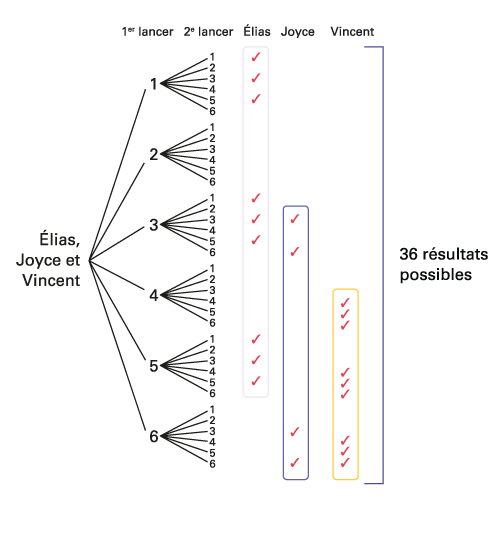image Six
branches se déploient à partir de l’ensemble de prénoms Élias, Joyce et Vincent. Elles correspondent au premier lancer
et sont chiffées d’un à six. À chacune d’elle, six branches se déploient; elles correspondent au deuxième lancer.
Élias obtient trois coches rouges vis-à-vis les ensembles de branches numéro un, trois et cinq, pour un total de 9.
Joyce obtient deux coches rouges vis-à-vis les ensembles de branches trois et cinq, pour un total de quatre. Ses
coches à elle sont encadrées en violet. Vincent obtient trois coches rouges vis-à-vis les ensembles de branches numéro
quatre, cinq et six pour un total de neuf. Ses coches à lui sont encadrées en jaune. L’arbre indique qu’il y a 36
résultats possibles.
\(P(Élias\ gagne)=\frac{nombre\ de\ résultats\ favorables}{nombre\ total\ de\ résultats\ possibles}\) \(=\ \frac{9}{36}\)
Je sais que 9 est un facteur commun de 9 et 36. Donc, je peux réduire la fraction en trouvant une fraction équivalente.
\(\frac{9\ \div\ 9}{36\ \div\ 9}=\frac{1}{4}\)
Je sais que je peux trouver le nombre décimal en effectuant une division.
\(1\div 4=0,25\)
Pour trouver le pourcentage, je dois effectuer une multiplication.
\(0,25\times 100 = 25\%\)
La probabilité théorique qu’Élias gagne est faible, soit 25 %.
\(P(Joyce\ gagne)=\frac{nombre\ de\ résultats\ favorables}{nombre\ total\ de\ résultats\ possibles}\) \(=\ \frac{4}{36}\)
Je sais que 4 est un facteur commun de 4 et 36. Donc, je peux réduire la fraction en trouvant une fraction équivalente.
\(\frac{4\ \div\ 4}{36\ \div\ 4}=\frac{1}{9}\)
Je sais que je peux trouver le nombre décimal en effectuant une division.
\(1\div 9=0,111\)
Pour trouver le pourcentage, je dois effectuer une multiplication.
\(0,111\times 100=11,1\%\)
La probabilité théorique que Joyce gagne est très faible, soit environ 11,1 %.
\(P(Vincent\ gagne)=\frac{nombre\ de\ résultats\ favorables}{nombre\ total\ de\ résultats\ possibles}\) \(=\ \frac{9}{36}\)
La probabilité théorique que Vincent gagne est de 25 %.
Élias et Vincent ont les meilleures chances de gagner étant donné que leur probabilité théorique de gagner, de 25 %, est plus élevée que celle de Joyce.
Stratégie 2 – Probabilité expérimentale
Je vais réaliser l’expérience en me servant d’un dé à six faces que je lancerai deux fois de suite, 150 fois en tout. Je note les résultats dans le tableau de probabilités pour ensuite inscrire le total pour chaque combinaison.
Voici un exemple de tableau :
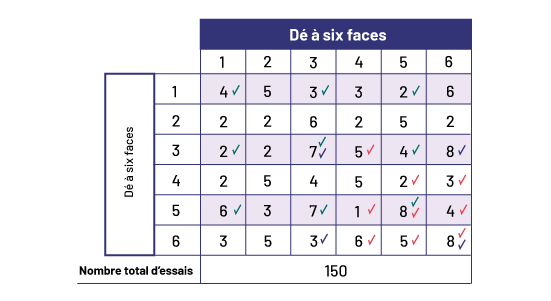image La
combinaison un-un a un résultat de 4, marqué d’une coche verte. La combinaison un-deux a un résultat de cinq. La
combinaison un-trois a un résultat de trois, marqué d’une coche verte. La combinaison un-quatre a un résultat de
trois. La combinaison un-cinq a un résultat de deux, marqué d’une coche verte. La combinaison un-six a un résultat de
six. La combinaison deux-un a un résultat de deux. La combinaison deux-deux a un résultat de deux. La combinaison
deux-trois a un résultat de six. La combinaison deux-quatre a un résultat de deux. La combinaison deux-cinq a un
résultat de cinq. La combinaison deux-six a un résultat de deux. La combinaison trois-un a un résultat de deux, marqué
d’une coche verte. La combinaison trois-deux a un résultat de deux. La combinaison trois-trois a un résultat de sept,
marqué d’une coche verte et d’une coche bleue. La combinaison trois-quatre a un résultat de cinq, marqué d’une coche
rouge. La combinaison trois-cinq a un résultat de quatre, marqué d’une coche verte. La combinaison trois-six a un
résultat de huit, marqué d’une coche bleue. La combinaison quatre-un a un résultat de deux. La combinaison quatre-deux
a un résultat de cinq. La combinaison quatre-trois a un résultat de quatre. La combinaison quatre-quatre a un résultat
de cinq. La combinaison quatre-cinq a un résultat de deux, marqué d’une coche rouge. La combinaison quatre-six a un
résultat de trois, marqué d’une coche rouge. La combinaison cinq-un a un résultat de six, marqué d’une coche verte. La
combinaison cinq-deux a un résultat de trois. La combinaison cinq-trois a un résultat de sept, marqué d’une coche
verte. La combinaison cinq-quatre a un résultat de un, marqué d’une coche rouge. La combinaison cinq-cinq a un
résultat de huit, marqué d’une coche verte et d’une coche rouge. La combinaison cinq-six a un résultat de quatre,
marqué d’une coche rouge. La combinaison six-un a un résultat de trois. La combinaison six-deux a un résultat de cinq.
La combinaison six-trois a un résultat de trois, marqué d’une coche bleue. La combinaison six-quatre a un résultat de
six, marqué d’une coche rouge. La combinaison six-cinq a un résultat de cinq, marqué d’une coche rouge. Et la
combinaison six-six a un résultat de huit, marqué d’une coche rouge et d’une coche bleue.
\(P(Élias\ gagne)=\frac{nombre\ d'essais\ favorables}{nombre\ total\ d'essais}\) \(=\ \frac{4\ +\ 3\ +\ 2\ +\ 2\ +\ 7\ +\ 4\ +\ 6\ +\ 7\ +\ 8}{150}\) \(=\ \frac{43}{150}=0,287=28,7\%\)
\(P(Joyce\ gagne)=\frac{nombre\ d'essais\ favorables}{nombre\ total\ d'essais}\) \(=\ \frac{7\ +\ 8\ +\ 3\ +\ 8}{150}\) \(=\ \frac{26}{150}=0,173=17,3\%\)
\(P(Vincent\ gagne)=\frac{nombre\ d'essais\ favorables}{nombre\ total\ d'essais}\) \(=\ \frac{5\ +\ 2\ +\ 3\ +\ 1\ +\ 8\ +\ 4\ +\ 6\ +\ 5\ +\ 8}{150}\) \(=\ \frac{42}{150}=0,28= 28\%\)
Selon les résultats que j’ai obtenus lors de l’expérience, la probabilité expérimentale qu’Élias gagne est d’environ 28,7 %, celle de Joyce est d’environ 17,3 % et celle de Vincent est de 28 %. Alors, Élias et Vincent ont les meilleures chances de gagner à ce jeu de hasard.
Exemple 2
Dans un sac, il y a trois cartes différentes : le six de trèfle, le neuf de cœur et le quatre de pique. Pietro tire une carte du sac, la remet dans le sac et en tire une seconde. Il gagne s’il tire deux cartes de suite qui sont des multiples de deux ou s’il tire deux fois la même carte.
Détermine la probabilité théorique que Pietro gagne.
Quelle est la probabilité expérimentale de cet événement?
Stratégie 1 – Probabilité théorique
Je dénombre les résultats possibles à l’aide d’un diagramme en arbre.
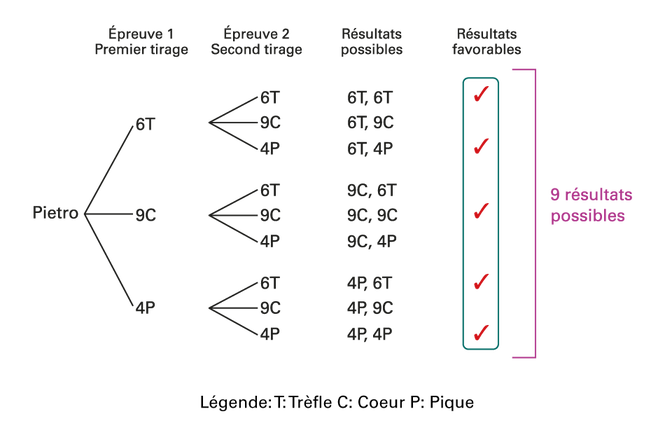image Légende : T égale trèfle, C égale coeur, et P égale pique. Le diagramme commence à partir du
nom Pietro, duquel trois branches se déploient. Elles correspondent à Épreuve un, premier tirage. La première donne
six T, la deuxième donne 9 C et la troisième donne quatre P. À partir de chacune des trois branches, trois autres
branches se déploient : 6 T, 9 C, quatre P. Elles correspondent à Épreuve deux, second tirage. Vient ensuite la
colonne des résultats possibles. En ordre : 6 T et 6 T. 6 T et 9 C. 6 T et 4 P. 9 C et 6 T. 9 C et 9 C. 9 C et 4 P.
4 P et 6 T. 4 P et 9 C. 4 P et 4 P. Vient ensuite la colonne « Résultats favorables ». Une coche rouge est placée à
côté des résultats suivants : 6 T et 6 T. 6 T et 4 P. 9 C et 9 C. 4 P et 6 T. 4 P et 4 P. L’arbre indique qu’il y a
9 résultats possibles.
\(P(Pietro\ gagne)=\frac{nombre\ de\ résultats\ favorables}{nombre\ total\ de\ résultats\ possibles}\) \(=\ \frac{5}{9}= 0,556 = 55,6\%\)
La probabilité théorique que Pietro gagne est d’environ 55,6 %.
Stratégie 2 – Probabilité expérimentale
Il s’agit d’une situation dans laquelle des cartes à jouer sont utilisées. Je prends les trois cartes nécessaires et je les place dans un sac opaque. Je tire une carte et je note le résultat. Je remets la carte dans le sac. Puis, je tire une seconde carte, je note le résultat et je remets la carte dans le sac. Je répète l’expérience 40 fois en vue de déterminer la probabilité expérimentale de l’événement.
Voici un exemple de tableau :
| Cartes à jouer | ||||
| Six de trèfle | Neuf de coeur | Quatre de pique | ||
| Cartes à jouer | Six de trèfle | 2 | 6 | 4 |
| Neuf de coeur | 6 | 4 | 3 | |
| Quatre de pique | 4 | 5 | 6 | |
| Nombre total d'essais | 40 | |||
\(P(Pietro\ gagne)=\frac{nombre\ d'essais\ favorables}{nombre\ total\ d'essais\ possibles}\) \(=\ \frac{2\ +\ 4\ +\ 4\ +\ 4\ +\ 6}{40}\) \(=\ \frac{20}{40}= 0,5= 50\%\)
Selon les résultats que j’ai obtenus lors de l’expérience, la probabilité expérimentale de gagner à ce jeu est équiprobable, soit de 50 %.
Source : En avant, les maths!, 6e année, ML, Données, p. 9.