D1.3 Choisir le diagramme le plus approprié pour représenter divers ensembles de données, y compris des diagrammes circulaires; représenter ces données à l’aide de diagrammes comprenant des sources, des titres, des étiquettes et des échelles appropriés; et justifier son choix.
ACTIVITÉ 1 : CHOIX DU DIAGRAMME LE PLUS APPROPRIÉ POUR REPRÉSENTER DES DONNÉES
Voici un tableau de fréquences relatives qui résume les résultats de l’élection provinciale du mois de juin 2022. Ces données secondaires ont été recueillies sur le site Web de Radio-Canada.
Résultat des élections ontariennes (juin 2022)
| Parti politique | Fréquence | Fréquence relative (%) |
|---|---|---|
|
Parti conservateur |
1 910 481 |
40,8 |
|
Nouveau Parti démocratique |
1 110 563 |
23,7 |
|
Parti libéral |
1 114 600 |
23,8 |
|
Parti vert |
278 975 |
6,0 |
|
Autres partis politiques |
263 408 |
5,6 |
|
Total |
4 678 027 |
99,9 |
Source : Résultats Élections Ontario 2022 | ICI Radio-Canada.ca.
Note : L’arrondissement des fréquences relatives en pourcentage au dixième près provoque une perte de précision, d’où la raison pour laquelle le total est de 99,9 % et non de 100 %. Il importe d’avoir une discussion avec les élèves sur l’effet de l’arrondissement sur les fréquences relatives.
Poser aux élèves la question suivante :
En analysant le tableau de fréquences relatives ci-dessus, quel type de diagramme représenterait le mieux les données qui s’y trouvent? Explique ton raisonnement.
Exemples de réponse
Élève A
En analysant le tableau ci-dessus, il est préférable d’utiliser un diagramme circulaire pour bien représenter les fréquences relatives. Ce diagramme représentera visuellement la portion de chaque catégorie au sein d’un ensemble (le total des votes). La taille de chaque secteur donnera une meilleure image de ce que les données représentent et facilitera ainsi leur interprétation. Il sera également possible de faire des liens avec des fractions et de mieux analyser les données dès le premier coup d’œil.
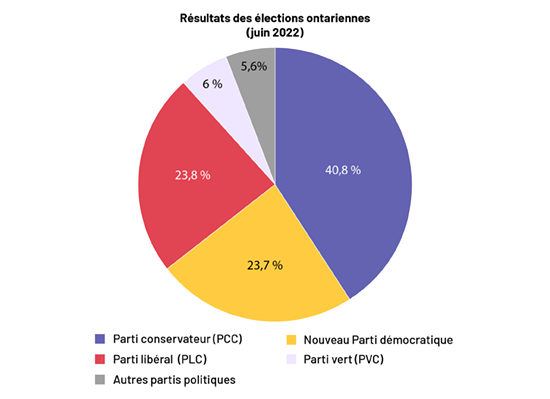
Après avoir construit le diagramme circulaire, on peut affirmer que le Parti conservateur a obtenu presque la moitié des suffrages (\(\frac{1}{2}\)). Quant au Parti libéral et au Nouveau Parti démocratique, 0,1 % seulement sépare le nombre de votes obtenus pour les deux partis. Pourtant, il y a une différence de 4 037 votes. En analysant le diagramme circulaire, nous constatons que ce dernier représente le mieux les données du tableau de fréquences relatives.
Élève B
En analysant le tableau ci-dessus, il est préférable d’utiliser un diagramme à bandes, puisque nous cherchons à représenter les données discrètes ainsi qu’à comparer la fréquence entre les diverses catégories.
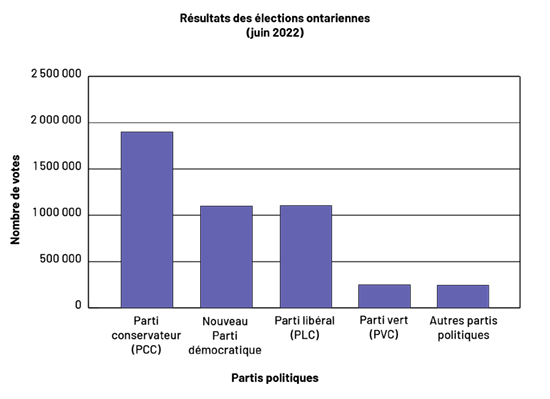
Après avoir construit le diagramme à bandes, on constate que près de 2 millions d’Ontariennes et d’Ontariens ont voté pour le Parti conservateur, contrairement à environ 1 million d’entre elles et eux qui ont voté pour le Nouveau Parti démocratique et le Parti libéral. Moins d’un million d’Ontariennes et d’Ontariens ont voté pour le Parti vert ainsi que pour les autres partis politiques. En analysant le diagramme, nous pouvons également affirmer qu’environ 5 millions d’entre elles et eux ont voté lors des élections de juin 2022, soit moins de la moitié des électrices et des électeurs inscrits sur les listes. Il serait d’ailleurs intéressant de comparer les données avec celles des dernières élections ontariennes, à savoir si chacun des partis politiques a remporté plus ou moins de votes depuis les élections de 2018. Pour arriver à ces fins, nous pourrions alors construire un diagramme à bandes multiples.
ACTIVITÉ 2 : DIAGRAMMES CIRCULAIRES FACILES À CONSTRUIRE
Presque tous les tableaux peuvent servir à construire des diagrammes circulaires. Il existe plusieurs façons de construire facilement ce type de diagramme sans recourir à un logiciel. Vous pouvez réaliser rapidement des diagrammes circulaires en faisant directement appel aux élèves du groupe-classe. Demandez-leur, par exemple, de nommer leur équipe de baseball favorite. Invitez-les ensuite à se mettre en ligne afin de regrouper celles et ceux qui ont nommé la même équipe. Par la suite, invitez les différents groupes à former un cercle. Fixez une des extrémités des quatre cordes sur le sol au moyen de ruban adhésif en un point correspondant au centre du cercle. Tendez ensuite chaque corde jusqu’à un point du cercle situé entre deux groupes d’élèves ayant choisi des équipes différentes. Voilà! Vous avez construit un très beau diagramme circulaire sans avoir pris des mesures ni calculé des pourcentages.
Exemple
Diagramme circulaire humain : les élèves forment un cercle et les cordes tendues séparent les différents groupes.
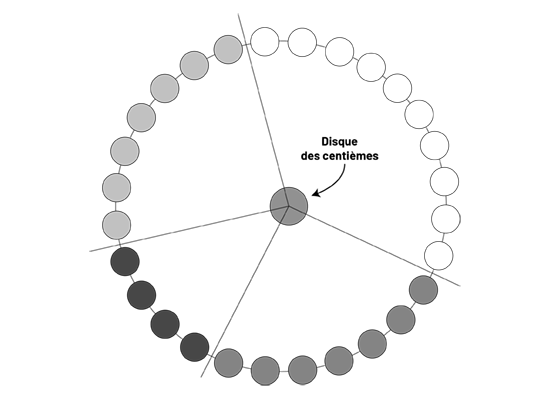
Copier le disque des centièmes (FR 3 : Disque des centièmes), le découper et le mettre au centre du cercle que forment les élèves : les ficelles délimitent chaque secteur du diagramme.
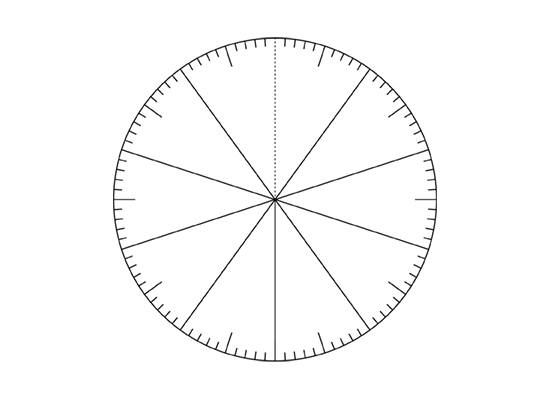
Il existe une autre façon simple de construire un diagramme circulaire, qui s’apparente au diagramme humain. Demandez d’abord aux élèves de construire un diagramme à barres pour représenter les données à interpréter. Ensuite, découpez les barres, puis les joindre bout à bout en utilisant du ruban adhésif. Enfin, joignez les deux extrémités à celles des segments préalablement réunis, puis tracez le cercle. Vous pouvez alors déterminer approximativement les pourcentages à l’aide de disque des centièmes, comme vous l’avez fait précédemment.
Source : Van de J. Walle et L. Lovin (2008). L’enseignement des mathématiques – L’élève au centre de son apprentissage, tome 3. Éditions du renouveau pédagogique inc., ISBN : 978-2-7613-2342-0, p. 351 et 397.
ACTIVITÉ 3 : REPRÉSENTER DES DONNÉES À L’AIDE D’UN DIAGRAMME CIRCULAIRE
Présenter aux élèves la mise en situation suivante :
Un sondage a été mené auprès de 25 000 jeunes Canadiennes et Canadiens de 12 à 17 ans pour connaître leurs habitudes relatives à la pratique d’activités physiques. Voici un tableau qui illustre les résultats :
| Pratique d’activités physiques chez les jeunes âgés de 12 à 17 ans | Fréquence | Fréquence relative (en nombre décimal) | Fréquence relative (en poucentage) |
|---|---|---|---|
| Actif (Pratique une activité physique plus de 4 fois par semaine) | 4 750 | 0,19 | 19 % |
| Moyennement actif (Pratique une activité physique environ 3 fois par semaine) | 9 000 | 0,36 | 36 % |
| Un peu actif (Pratique une activité physique environ 2 fois par semaine) | 1 500 | 0,06 | 6 % |
| Très peu actif (Pratique une activité physique environ 1 fois par semaine) | 6 500 | 0,26 | 26 % |
| Inactif (Pratique occasionnelle d'activités physiques ou aucune pratique) | 3 250 | 0,13 | 13 % |
| Total | 25 000 | 1,0 | 100 % |
Représente les résultats du tableau de fréquences relatives sous la forme d’un diagramme circulaire. Avant de commencer, ordonne d’abord les catégories de la plus grande à la plus petite en fonction de ce que tu anticipes être la taille de chaque section du cercle.
Stratégie
Avant de créer le diagramme circulaire, les catégories sont ordonnées de la plus grande à la plus petite en fonction de la taille estimée de chaque section du cercle. La plus grande section du cercle sera probablement occupée par la catégorie « Moyennement actif » parce qu’il s’agit de la fréquence relative la plus élevée dans le tableau, soit 36 %. Voici les catégories qui devraient suivre :
- 2e section du diagramme : Très peu actif (26 %)
- 3e section du diagramme : Actif (19 %)
- 4e section du digramme : Inactif (13 %)
- 5e section du diagramme : Un peu actif (6 %)
Pour créer un diagramme circulaire, nous devons mesurer l’angle au degré le plus proche de chaque secteur.
| Pratique d’activités physiques chez les jeunes âgés de 12 à 17 ans | Fréquence | Fréquence relative (en nombre décimal) | Fréquence relative (en poucentage) | Mesure de l'angle (au degré près) |
|---|---|---|---|---|
| Actif (Pratique une activité physique plus de 4 fois par semaine) | 4 750 | 0,19 | 19 % | \({\begin{align} 19\% \times 360 \\ 0,19 \times 360 = 68° \end{align}}\) |
| Moyennement actif (Pratique une activité physique environ 3 fois par semaine) | 9 000 | 0,36 | 36 % | \({\begin{align} 36\% \times 360 \\ 0,36 \times 360 = 130° \end{align}}\) |
| Un peu actif (Pratique une activité physique environ 2 fois par semaine) | 1 500 | 0,06 | 6 % | \({\begin{align} 6\% \times 360 \\ 0,06 \times 360 = 22° \end{align}}\) |
| Très peu actif (Pratique une activité physique environ 1 fois par semaine) | 6 500 | 0,26 | 26 % | \({\begin{align} 26\% \times 360 \\ 0,26 \times 360 = 93° \end{align}}\) |
| Inactif (Pratique occasionnelle d'activités physiques ou aucune pratique) | 3 250 | 0,13 | 13 % | \({\begin{align} 13\% \times 360 \\ 0,13 \times 360 = 47° \end{align}}\) |
| Total | 25 000 | 1,0 | 100 % | 360° |
Note : Dans le tableau de fréquences, la colonne Mesure de l’angle est nécessaire uniquement lorsque le diagramme circulaire est construit à la main. Tracez un cercle sur une feuille à l’aide d’un compas et utilisez un rapporteur pour séparer le cercle en secteurs selon les mesures d’angle calculées. Pour trouver la mesure de l’angle représentant chaque secteur, multipliez la fréquence relative en pourcentage par 360, puisqu’un cercle mesure 360 o.
Seules les colonnes Activités physiques que pratiquent les jeunes de 12 à 17 ans et Fréquence ou Fréquence en pourcentage sont nécessaires lorsque le diagramme circulaire est construit à l’aide d’un tableur. On insère les données dans le tableur en s’assurant de ne pas ajouter la rangée Total.
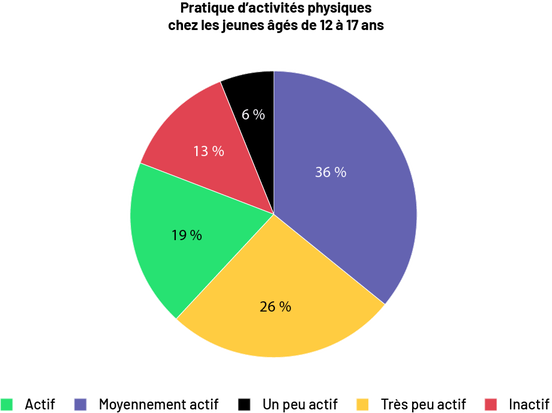
Les résultats peuvent maintenant être représentés sous la forme d’un diagramme circulaire. Le diagramme circulaire doit comprendre les éléments suivants :
- titre : Pratique d’activités physiques chez les jeunes âgés de 12 à 17 ans;
- cercle divisé en cinq secteurs adjacents;
- désignation des secteurs à l’aide de pourcentages : 36 %, 26 %, 19 %, 13 %, 6 %;
- désignation des secteurs en fonction des catégories : Actif, Moyennement actif, Un peu actif, Très peu actif et Inactif.
Source : En avant, les maths!, 7e année, CM, Données, p. 5-8.
