D2.2 Déterminer et comparer les probabilités théoriques et expérimentales que deux événements indépendants se produisent et que deux événements dépendants se produisent.
ACTIVITÉ 1 : DÉTERMINER LES PROBABILITÉS THÉORIQUES ET EXPÉRIMENTALES
En utilisant un jeu comprenant les cartes suivantes :
- déterminer les probabilités théoriques et expérimentales (10 essais et 20 essais) de tirer deux rois consécutifs si la première carte tirée est remise dans le paquet (événements indépendants);
- déterminer les probabilités théoriques et expérimentales (10 essais et 20 essais) de tirer deux rois consécutifs si la première carte tirée n’est pas remise dans le paquet (événements dépendants).
Pistes de questionnement :
- Est-ce que la probabilité de tirer deux rois consécutifs est plus élevée lors d’événements indépendants ou d’événements dépendants? Pourquoi?
- Comment peux-tu comparer les probabilités expérimentales aux probabilités théoriques? Comment le nombre d’essais affecte cette comparaison?
ACTIVITÉ 2 : COMPARER LES PROBABILITÉS THÉORIQUES ET EXPÉRIMENTALES
Voici les probabilités théoriques et expérimentales (10 essais et 20 essais) d’événements indépendants. L’activité consistait à déterminer les probabilités de tirer 2 jetons bleus consécutifs si le premier jeton est remis dans le sac. Le sac contenait 2 jetons jaunes, 2 jetons verts et 6 jetons bleus.
Probabilité théorique
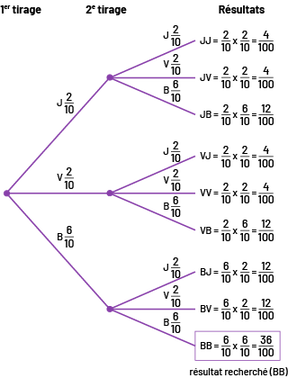Image Si au premier tirage, on a deux probabilités sur dix de piger un jeton jaune, et qu’au deuxième tirage, on a deux probabilités sur dix de piger un jeton jaune, le résultat est : deux sur dix multiplié par deux sur dix égale quatre probabilités sur cent de piger deux jetons jaunes.Si au deuxième tirage on a deux probabilités sur dix de piger un jeton vert, le résultat est : deux sur dix multiplié par deux sur dix égale quatre probabilités sur cent de piger un jeton jaune puis un jeton vert. Si au deuxième tirage, on a six probabilités sur dix de piger un jeton bleu, le résultat est : deux sur dix multiplié par six sur dix égale douze chances sur cent de piger un jeton jaune puis un jeton bleu. Si au premier tirage on a deux probabilités sur dix de piger un jeton vert, et qu’au deuxième tirage, on a deux probabilités sur dix de pigner un jeton jaune, le résultat est : deux sur dix multiplié par deux sur dix égale quatre probabilités sur cent de piger un jeton vert puis un jeton jaune. Si au deuxième tirage on a deux probabilités sur dix de piger un jeton vert, le résultat est : deux sur dix multiplié par deux sur dix égale quatre probabilités sur cent de piger deux jetons verts. Si au deuxième tirage on a six probabilités sur dix de piger un jeton bleu, le résultat est : deux sur dix multiplié par six sur dix égale douze probabilités sur cent de piger un jeton vert puis un jeton bleu. Si au premier tirage on a six probabilités sur dix de piger un jeton bleu, et qu’au deuxième tirage, on a deux probabilités sur dix de piger un jeton jaune, le résultat est : six sur dix multiplié par deux sur dix égale douze probabilités sur cent de piger un jeton bleu puis un jeton jaune. Si au deuxième tirage on a deux probabilités sur dix de piger un jeton vert, le résultat est : six sur dix multiplié par deux sur dix égale douze probabilités sur cent de piger un jeton bleu puis un jeton vert. Si au deuxième tirage on a six probabilités sur dix de piger un jeton bleu, le résultat est : six sur dix multiplié par six sur dix égale 36 probabilités sur cent de piger deux jetons bleus. Cette dernière équation est la seule de toutes les équations du diagramme à être encadrée.
Probabilité expérimentale
Tableaux de fréquences relatives
Tirer 2 jetons bleus consécutifs en remettant dans le sac le premier jeton tiré (10 essais).
Résultats de l'expérience : J, BJ, V, BB, BV, V, BB, J, BJ, BB.
| Combinaison de jetons | Dénombrement | Fréquence | Fréquence (fraction) | Fréquence (pourcentage) |
|---|---|---|---|---|
| J |
|| |
2 | \(\frac{2}{10}\) | \(\displaylines{\begin{align} \frac{2}{10} &= 2 \div 10 \\ &= 0,2 \\ &= 20 \% \end{align}}\) |
| BJ |
|| |
2 | \(\frac{2}{10}\) | \(\displaylines{\begin{align} \frac{2}{10} &= 2 \div 10 \\ &= 0,2 \\ &= 20 \% \end{align}}\) |
| V |
|| |
2 | \(\frac{2}{10}\) | \(\displaylines{\begin{align} \frac{2}{10} &= 2 \div 10 \\ &= 0,2 \\ &= 20 \% \end{align}}\) |
| BB |
||| |
3 | \(\frac{3}{10}\) | \(\displaylines{\begin{align} \frac{3}{10} &= 3 \div 10 \\ &= 0,3 \\ &= 30 \% \end{align}}\) |
| BV |
| |
1 | \(\frac{1}{10}\) | \(\displaylines{\begin{align} \frac{1}{10} &= 1 \div 10 \\ &= 0,1 \\ &= 10 \% \end{align}}\) |
| Total | 10 | 10 | \(\frac{10}{10}\) | 100 % |
Note : Dans les tableaux, il faut écrire la couleur du jeton tiré chaque fois qu’un premier tirage est effectué. Si, au premier tirage, un jeton bleu est obtenu, il faut procéder à un second tirage. Si un jeton d’une autre couleur est tiré, il n’est pas nécessaire de tirer un autre jeton, car c’est déjà perdu.
Tirer 2 jetons bleus consécutifs en remettant dans le sac le premier jeton tiré (20 essais).
Résultats de l'expérience : BB, J, V, BB, BJ, V, BV, J, BB, BB, J, BV, BJ, V, BB, V, BJ, BB, BB, J.
| Combinaison de jetons | Dénombrement | Fréquence | Fréquence (fraction) | Fréquence (pourcentage) |
|---|---|---|---|---|
| BB |
|||| ||| |
7 | \(\frac{7}{20}\) | \(\displaylines{\begin{align} \frac{7}{20} &= 7 \div 20 \\ &= 0,35 \\ &= 35 \% \end{align}}\) |
| J |
|||| |
4 | \(\frac{4}{20}\) | \(\displaylines{\begin{align} \frac{4}{20} &= 4 \div 20 \\ &= 0,2 \\ &= 20 \% \end{align}}\) |
| BV |
|| |
2 | \(\frac{2}{20}\) | \(\displaylines{\begin{align} \frac{2}{20} &= 2 \div 20 \\ &= 0,1 \\ &= 10 \% \end{align}}\) |
| V |
|||| |
4 | \(\frac{4}{20}\) | \(\displaylines{\begin{align} \frac{4}{20} &= 4 \div 20 \\ &= 0,2 \\ &= 20 \% \end{align}}\) |
| BJ |
||| |
3 | \(\frac{3}{20}\) | \(\displaylines{\begin{align} \frac{3}{20} &= 3 \div 20 \\ &= 0,15 \\ &= 15 \% \end{align}}\) |
| Total | 20 | 20 | \(\frac{20}{20}\) | 100 % |
Source : En avant, les maths!, 7e année, ML, Données, p. 5-8.
Demander aux élèves d’analyser et de comparer la probabilité théorique et les probabilités expérimentales d’obtenir deux jetons bleus consécutifs. Voici d’autres exemples de questions à leur poser afin de pousser leur raisonnement :
- Si tu compares la probabilité expérimentale d’obtenir deux jetons bleus consécutifs après 10 essais avec celle obtenue après 20 essais, que remarques-tu?
- Que remarques-tu en comparant la probabilité expérimentale comportant 10 essais et celle comportant 20 essais avec la probabilité théorique?
- Que remarques-tu si tu additionnes ou si tu compares la somme des probabilités des résultats obtenus pour chacun des tableaux de fréquences relatives et le diagramme en arbre?
Encourager les élèves à déterminer la probabilité théorique et les probabilités expérimentales (10 essais et 20 essais) de tirer deux jetons bleus si le premier jeton tiré n’est pas remis dans le sac (événements dépendants). Leur demander de comparer les probabilités obtenues avec celles calculées précédemment lors des événements indépendants.