D1.5 Utiliser le vocabulaire mathématique, y compris des termes comme « forte », « faible », « nulle », « positive » et « négative » pour décrire la relation entre deux variables appartenant à divers ensembles de données, comprenant ou non des données aberrantes.
ACTIVITÉ 1 : RELATIONS ENTRE DEUX VARIABLES
Activité d’une compétition de bolo avec les élèves
Les élèves d’une classe ont tenu une compétition de bolo lors d’une journée spéciale.
Le but était de frapper la balle le plus de fois possible et aussi longtemps que possible sans manquer un coup.
Le tableau ci-dessous représente le résultat de 15 élèves.
| Durée en secondes | Nombre de frappes |
|---|---|
| 14 | 28 |
| 12 | 24 |
| 15 | 75 |
| 48 | 48 |
| 28 | 84 |
| 20 | 40 |
| 44 | 132 |
| 22 | 110 |
| 36 | 180 |
| 50 | 200 |
| 57 | 114 |
| 30 | 120 |
| 6 | 24 |
| 25 | 25 |
| 39 | 156 |
Les données sont entrées dans un diagramme à nuage de points pour voir s’il y a une corrélation entre le nombre de frappes et la durée.
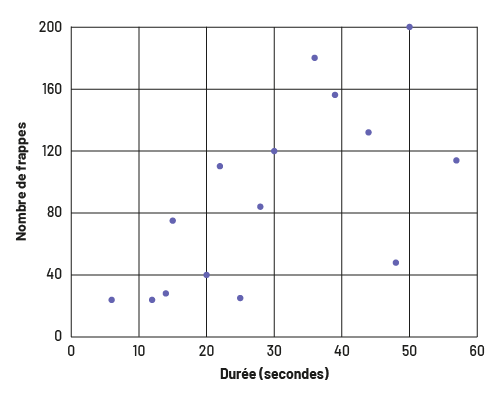 image Le diagramme de dispersion s’intitule « Au bolo ». Gradué de zéro à 60, l’axe horizontal se nomme « Durée en secondes », et l’axe vertical, gradué de zéro à 200, se nomme « Nombre de frappes ». Le point le plus haut sur l’axe vertical se situe à 200 frappes.
image Le diagramme de dispersion s’intitule « Au bolo ». Gradué de zéro à 60, l’axe horizontal se nomme « Durée en secondes », et l’axe vertical, gradué de zéro à 200, se nomme « Nombre de frappes ». Le point le plus haut sur l’axe vertical se situe à 200 frappes.- Est-ce que les points sont très regroupés autour d’une ligne droite?
- Est-ce que les points sont plus ou moins regroupés autour d’une ligne droite?
- Si une variable augmente, qu’arrive-t-il à l’autre variable?
Les points sont plutôt dispersés autour d’une ligne qui va du coin inférieur gauche au coin supérieur droit. Il y a donc une faible relation entre les données.
Cela indique que le degré de corrélation entre le nombre de frappes et la durée n’est pas très élevé.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 2 : VOCABULAIRE ASSOCIÉ AUX RELATIONS ENTRE DEUX VARIABLES
Utiliser les termes appropriés (faible ou forte relation positive, faible ou forte relation négative, relation nulle et diagramme avec données aberrantes) pour décrire la relation entre les deux variables dans les diagrammes ci-dessous. Expliquer son choix.
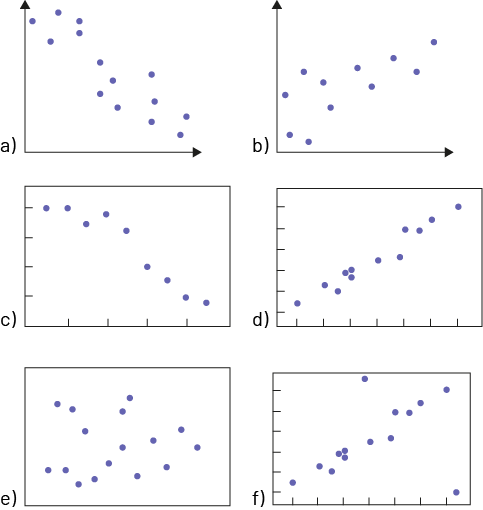
Exemples de réponses
a) On remarque que plus la variable représentée sur l’axe horizontal augmente, plus la variable représentée sur l’axe vertical diminue. On sait donc qu’il s’agit d’une relation négative. De plus, on observe que les points sont dispersés, donc on peut en déduire qu’il s’agit d’une faible relation négative.
b) On remarque que plus la variable représentée sur l’axe horizontal augmente, plus la variable représentée sur l’axe vertical augmente également. On sait donc qu’il s’agit d’une relation qui est positive. De plus, on observe que les points sont dispersés, donc on peut en déduire qu’il s’agit d’une faible relation positive.
c) On remarque que plus la variable représentée sur l’axe horizontal augmente, plus la variable représentée sur l’axe vertical diminue. On sait donc qu’il s’agit d’une relation négative. De plus, on observe que les points ne sont pas du tout dispersés et qu’ils sont ordonnés de manière à ressembler à une droite. On peut donc en déduire qu’il s’agit d’une forte relation négative.
d) On remarque que plus la variable représentée sur l’axe horizontal augmente, plus la variable représentée sur l’axe vertical augmente également. On sait donc qu’il s’agit d’une relation positive. De plus, on observe que les points ne sont pas du tout dispersés et qu’ils sont ordonnés de manière à ressembler à une droite. On peut donc en déduire qu’il s’agit d’une forte relation positive.
e) On remarque que les points sont complètement dispersés et qu’il n’y a aucun lien entre les deux variables. On peut donc conclure qu’il y a une relation nulle entre les deux variables.
f) On remarque qu’il semble y avoir des données qui sont complètement à l’écart de la tendance des autres données. On peut donc déduire qu’il s’agit d’un diagramme qui contient des données aberrantes.
Source : En avant, les maths!, 8e année, CM, Données p. 3-4.
