D1.5 Utiliser le vocabulaire mathématique, y compris des termes comme « forte », « faible », « nulle », « positive » et « négative » pour décrire la relation entre deux variables appartenant à divers ensembles de données, comprenant ou non des données aberrantes.
HABILETÉ : DÉCRIRE LA RELATION ENTRE DEUX VARIABLES APPARTENANT À DIVERS ENSEMBLES DE DONNÉES, COMPRENANT OU NON DES DONNÉES ABERRANTES
Lors de l’analyse des données à partir du diagramme de dispersion, les élèves observent la disposition des points afin de décrire les relations qui s’y trouvent (ou non) entre les deux variables étudiées.
Lorsque les points de données sont ordonnés de manière à presque former une droite ou une courbe, cela indique une forte relation (positive ou négative). Lorsque les points de données sont très dispersés, cela indique une absence de relation.
Parfois, il faut faire abstraction d’une donnée aberrante pour obtenir une droite ou une courbe bien ajustée avec les autres points de données. C’est la raison pour laquelle il est important de déterminer d’abord les données aberrantes sur le diagramme et de les éliminer avant d’effectuer un ajustement de courbe.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Le diagramme de dispersion, aussi appelé le nuage de points, permet d’analyser des relations entre des variables. Les élèves peuvent donc visualiser les points sur le diagramme et décrire la relation entre deux variables en utilisant des termes comme « forte », « faible », « nulle », « positive » et « négative ».
En science, le nuage de points est grandement utilisé pour présenter la mesure de deux ou plusieurs variables liées. Le nuage de points est particulièrement utile lorsque les valeurs des variables sur l’axe des y dépendent des valeurs de la variable de l’axe des x.
Dans un nuage de points, les points sont placés sans être reliés. La tendance qui en résulte indique le type et la force de la relation entre deux ou plusieurs variables.
La représentation graphique suivante est un exemple de nuage de points. Le pourcentage de gens qui possèdent une voiture augmente avec le revenu, ce qui montre une relation positive entre ces deux variables.
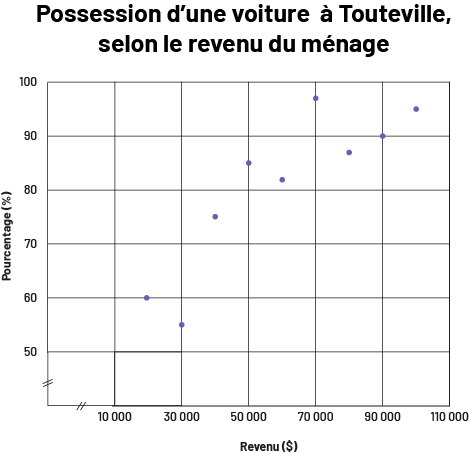image Le diagramme de dispersion s’intitule « Possession d’une voiture à Touteville, selon le revenu du ménage ». L’axe horizontal est gradué de 10 000 à 110 000 et se nomme « Revenu en dollars ». L’axe vertical est gradué de 50 à 100 et se nomme « Pourcentage ». Les points ont tendance à former une diagonale ascendante.
| Revenu ($) | Pourcentage (%) |
|---|---|
| 20 000 | 60 |
| 30 000 | 55 |
| 40 000 | 75 |
| 50 000 | 85 |
| 60 000 | 82 |
| 70 000 | 97 |
| 80 000 | 87 |
| 90 000 | 90 |
| 100 000 | 95 |
La tendance des points du nuage montre la relation entre les variables. Les nuages de points peuvent montrer différentes tendances et relations, par exemple :
- une relation linéaire ou non linéaire : Lorsque les points forment une ligne droite dans le diagramme, la relation entre les variables est linéaire, comme dans le diagramme A. Lorsque les points ne forment pas de ligne ou forment une ligne qui n’est pas droite comme dans le diagramme B, la relation n’est pas linéaire.
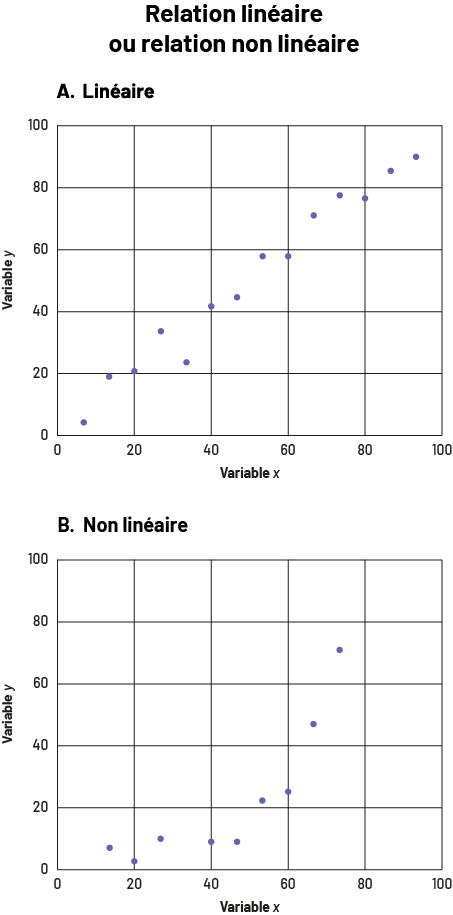image Deux diagrammes de dispersion sont placés l’un sous l’autre. Le titre commun est « Relation linéaire ou relation non linéaire ». Les axes se nomment « Variable X » et « Variable Y » et sont gradués de zéro à 100. Le graphique « A » est linéaire et les points forment une diagonale ascendante. Le graphique « B » est non linéaire et les points s’alignent d’abord horizontalement avant de montrer une tendance ascendante sur l’axe vertical.
- une relation positive ou négative : Si les points sont regroupés près d’une ligne qui va du coin inférieur gauche au coin supérieur droit du diagramme, la relation entre les deux variables est dite positive (diagramme A). Si les points sont regroupés près d’une ligne qui va du coin supérieur gauche au coin inférieur droit du diagramme, la relation entre les variables est dite négative (diagramme B).
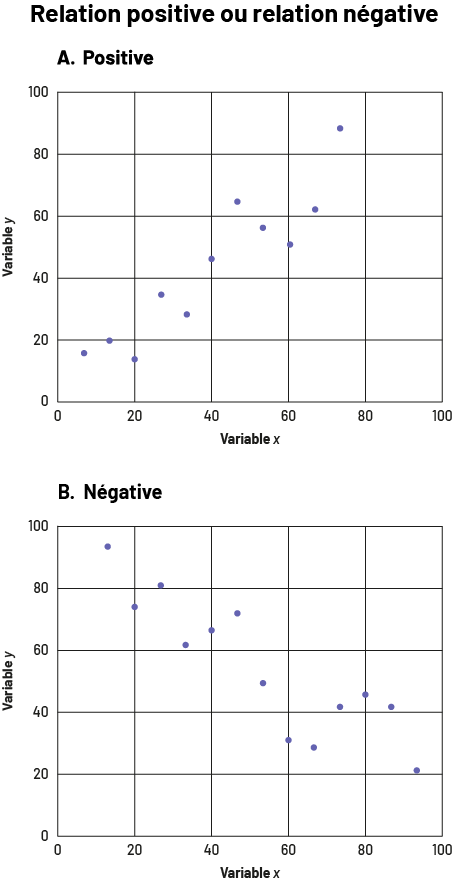image Deux diagrammes de dispersion sont placés l’un sous l’autre. Le titre commun est « Relation positive ou relation négative ». Les axes se nomment « Variable X » et « Variable Y » et sont gradués de zéro à 100. Le graphique « A » a une relation positive; les points sont groupés de façon à former une diagonale ascendante. Le graphique « B » a une relation négative; les points sont groupés de façon à former une diagonale descendante.
- la concentration ou la dispersion des données : Les points peuvent être très près les uns des autres (diagramme A) ou être très dispersés dans l’espace (diagramme B).
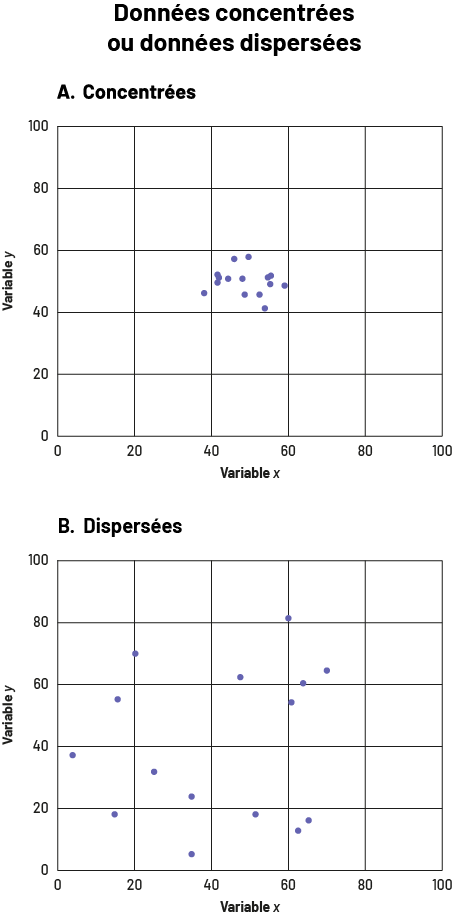image Deux diagrammes de dispersion sont placés l’un sous l’autre. Le titre commun est « Données concentrées ou données dispersées ». Les axes se nomment « Variable X » et « Variable Y » et sont gradués de zéro à 100. Le graphique « A » présente des données concentrées. Tous les points sont regroupés dans la même case sauf un, qui se situe quand même très près des autres. Le graphique « B » présente des données dispersées; les points sont éloignés les uns des autres.
- la présence de valeurs extrêmes (aberrantes) : En plus de montrer la relation entre deux variables, un nuage de points peut également montrer des valeurs extrêmes dans l’ensemble de données. Les valeurs extrêmes sont celles qui sont éloignées des autres données de l’ensemble de données, comme les deux points en rouge dans le diagramme.
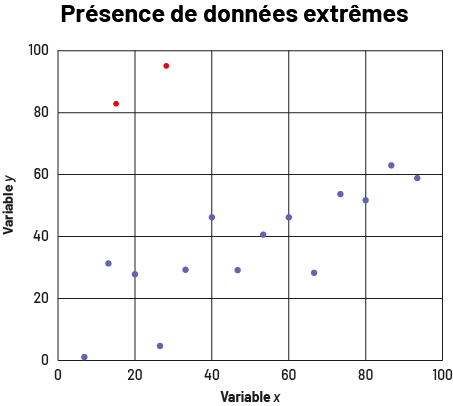image Le diagramme de dispersion s’intitule « Présente de données extrêmes ». Les axes se nomment « Variable X » et « Variable Y » et sont gradués de zéro à 100. Les quatorze points violets se répartissent entre zéro et cent sur l’axe horizontal, et entre zéro et 70 sur l’axe vertical; tandis que deux points rouges se trouvent entre zéro et 40 sur l’axe horizontal, et entre 80 et cent sur l’axe vertical.