B1.6 Utiliser des schémas pour représenter et résoudre des problèmes de partage équitable d’une quantité entre 2 et 4 personnes, avec un reste de 1 ou de 2.
Activité 1 : partage équitable d’objets entre deux personnes
Présenter aux élèves l’illustration suivante.
Former des groupes de deux. Demander à chacun des groupes de se partager équitablement le nombre de billes en utilisant du matériel de manipulation ou des collections d’objets.
Circuler parmi les élèves leur poser des questions telles que :
- Que remarque-t-on?
- Comment peut-on diviser les billes de sorte que chaque personne reçoive la même quantité? Quelles stratégies peut-on utiliser?
- Lorsqu’on divise le nombre de billes de façon équitable, reste-t-il des billes? Si oui, que peut-on faire avec la bille restante? Explique ton raisonnement.
Activité 2 : partage équitable d’objets entre quatre personnes
Les parents de Jamila, de Fadila, de Chafi et de Nazim préparent les collations pour la semaine. Ils ont acheté une boîte de 18 barres tendres. Ils comptent mettre, dans le sac-repas de chaque enfant, une barre tendre par jour. Comment pourraient-ils partager de façon équitable les barres tendres?
Stratégie 1
L’élève utilise des rectangles pour montrer le partage équitable de 18 barres tendres entre les 4 enfants de la famille.
En premier, l’élève remet 4 barres tendres entières à chaque enfant. Il reste deux barres tendres à partager équitablement. L’élève divise chaque rectangle en deux parties égales (carrés) et remet une moitié à chaque enfant. Alors, pour un partage équitable, chaque enfant reçoit 4 barres tendres et un demi.
Stratégie 2
L’élève peut distribuer les 18 barres tendres tout en assurant un partage équitable entre les 4 enfants. Les enfants auront chacune ou chacun 4 barres tendres. Il reste deux barres à partager. L’élève peut alors décider de diviser les deux dernières barres en deux afin de créer un demi-morceau supplémentaire pour chaque enfant. Ainsi, chaque enfant aura 4 et une demie barres tendres.
image Chacun accompagné d’un ensemble de quatre barres tendres, les noms Jamila, Fadila, Chafi et Nazim sont écrits l’un sous l’autre. Un trait rouge relie tous les ensembles de quatre barres tendres. À côté du trait, il y a deux barres tendres divisées en deux parts égales par un trait bleu.
Stratégie 3
L’élève peut utiliser 18 jetons pour représenter les barres tendres. Elle ou il peut distribuer les jetons équitablement entre les 4 enfants. Chaque enfant de la famille reçoit alors 4 jetons. Il en reste deux. Puisque nous pouvons couper une barre tendre en deux, il est possible de partager de façon équitable les deux barres qui restent entre les 4 enfants. Chaque enfant aura alors 4 et une demie barres tendres.
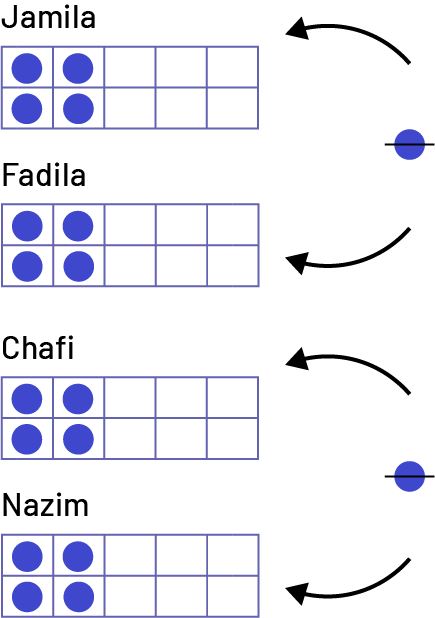image Les prénoms Jamila, Fadila, Chafi et Nazim, placés l’un sous l’autre, sont respectivement associés à une grille composée de deux rangées de cinq cases. Il y a quatre jetons dans chacune des grilles. Entre les prénoms Jamila et Fadila, il y a un jeton séparé en deux par un trait, duquel deux flèches pointent respectivement vers les prénoms Jamila et Fadila. Entre les prénoms Chafi et Nazim, il y a un jeton séparé en deux par un trait, duquel deux flèches pointent respectivement vers les prénoms Chafi et Nazim.
Poser aux élèves des questions telles que :
- En comparant les différentes stratégies des élèves, que remarque-t-on?
- Est-il possible de partager équitablement les 18 barres tendres entre les 4 enfants? Reste-t-il des barres tendres? Comment le sais-tu?
- S’il reste des barres tendres, comment peut-on s’y prendre pour les diviser de façon équitable? Explique ta démarche.
- À l’aide de mots, comment peut-on décrire les parts résultant du partage?