B2.3 Utiliser des stratégies de calcul mental, y compris l’estimation, pour additionner des nombres naturels dont la somme est égale ou inférieure à 20 et pour soustraire des nombres égaux ou inférieurs à 20, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental
La résolution de problèmes à l’aide du calcul mental est souvent un bon moyen d’inciter les élèves à élaborer des manières plus efficientes de faire des calculs sur papier. Le personnel enseignant peut encourager les élèves à recourir au calcul mental en présentant les équations horizontalement (\(\ 14 + 6\)) plutôt que verticalement :
Les élèves qui prennent le temps d’observer les nombres et de penser à la meilleure façon de résoudre l’équation avant de commencer à faire quoi que ce soit sur papier sont plus susceptibles de choisir la méthode la plus efficiente pour résoudre l’équation. Par exemple, un moment de réflexion avant de calculer \(11 + 9\) peut aider les élèves à se rendre compte qu’il est très facile de combiner le 1 avec 9 pour faire 10, puis d’ajouter le 10 qui reste pour arriver à la réponse, soit 20. Devant un calcul, les élèves utilisent souvent, mais pas toujours, des stratégies souples dans leur tête et prennent, au besoin, quelques notes écrites pour visualiser leur cheminement.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 40-41.
Les stratégies personnelles développées par l’élève deviennent avec le temps ses stratégies de calcul mental.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 38.
Il est donc important que le personnel enseignant offre de nombreuses expériences pour que les élèves se familiarisent avec les stratégies de calcul mental afin qu’elles et ils apprennent les faits numériques de base relatifs à l’addition et à la soustraction.
Lorsque les élèves constatent que les stratégies apprises en travaillant avec des nombres à un chiffre peuvent aussi s’appliquer aux nombres à plusieurs chiffres, leur compréhension des opérations sur les nombres à plusieurs chiffres s’améliore. Aussi faut-il les aider à établir cette relation.
Une façon de faire consiste à modeler l’utilisation d’une stratégie de calcul mental connue se rattachant aux faits numériques de base et de l’adapter pour inclure des nombres à plusieurs chiffres. On peut, par exemple, revoir avec les élèves les stratégies pour apprendre les faits numériques de base relatifs à l’addition et à la soustraction, tout en les adaptant pour des nombres à plusieurs chiffres.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 48.
Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec la soustraction.
 Description de la vidéo
Description de la vidéo
Description à venir
Faire du calcul mental signifie déterminer la représentation d’un nombre qui est la plus utile pour effectuer un calcul particulier. Utiliser des modèles pour représenter les nombres et les faits numériques de base peut aider les élèves à comprendre le sens des opérations fondamentales et à en amoindrir le caractère abstrait, comme le cadre à dix cases, la droite numérique et la grille de nombres.
Les modèles aident les élèves à établir des relations et ainsi à mieux comprendre ce que les symboles représentent dans les opérations.
Le personnel enseignant peut aider les élèves à relier leur compréhension du problème d’abord avec du matériel de manipulation, puis avec des symboles comme les signes =, + et –, pour ensuite calculer mentalement.
« 1 de plus » et « 2 de plus »
Dans les faits numériques de base \(\ 5 + 1 = 6\), \(\ 5 + 2 = 7\), \(\ 7 + 1 = 8\), \(\ 7 + 2 = 9\), l’un des termes de chaque addition est 1 ou 2. La stratégie repose sur l’hypothèse que les élèves se rappellent facilement le nombre qui suit et celui qui vient après.
image Au-dessus de la grille onze par onze, il est écrit « un de plus, deux de plus ». Dans le coin en haut à gauche, il y a le symbole plus. Les colonnes et les rangées se chiffrent respectivement de zéro à neuf. La rangée et la colonne zéro se chiffrent de zéro à neuf. La rangée et la colonne un se chiffrent d’un à dix. La rangée et la colonne deux se chiffrent de deux à onze. La rangée et la colonne trois se chiffrent de trois à douze. La rangée et la colonne quatre se chiffrent de quatre à treize. La rangée et la colonne cinq se chiffrent de cinq à 14. La rangée et la colonne six se chiffrent de six à 15. La rangée et la colonne sept se chiffrent de sept à 16. La rangée et la colonne huit se chiffrent de huit à 17. Et la rangée et la colonne neuf se chiffrent de neuf à 18.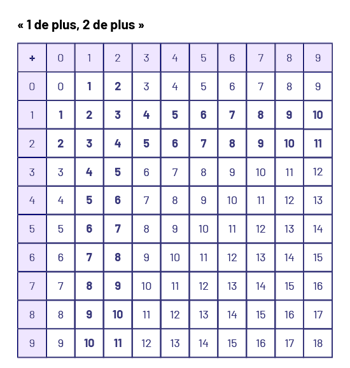
Faits numériques avec 0 (\(\ 1 + 0 = 1\), \(\ 1 – 0 = 1\))
Dans ces faits numériques de base, 0 est l’un des termes de chaque addition et de chaque soustraction. Les élèves généralisent souvent trop en pensant que la réponse à une addition est nécessairement plus grande et que la réponse à une soustraction est nécessairement plus petite. On peut renforcer la compréhension du concept de neutralité du zéro dans l’addition et dans la soustraction à l’aide de jeux où l’on fait usage de cartes-éclairs et de cubes numérotés.
image La grille chiffrée s’intitule Faits numériques de base avec zéro.Dans le coin en haut à gauche, il y a le symbole plus. Les colonnes et les rangées se chiffrent respectivement de zéro à neuf. La rangée et la colonne zéro se chiffrent de zéro à neuf. La rangée et la colonne un se chiffrent d’un à dix. La rangée et la colonne deux se chiffrent de deux à onze. La rangée et la colonne trois se chiffrent de trois à douze. La rangée et la colonne quatre se chiffrent de quatre à treize. La rangée et la colonne cinq se chiffrent de cinq à 14. La rangée et la colonne six se chiffrent de six à 15. La rangée et la colonne sept se chiffrent de sept à 16. La rangée et la colonne huit se chiffrent de huit à 17. Et la rangée et la colonne neuf se chiffrent de neuf à 18.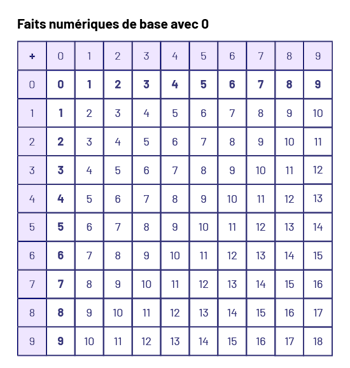
Utilisation des doubles
Dans ces faits numériques de base, le premier terme et le deuxième terme (ou les deux termes) sont les mêmes. Il est avantageux pour les élèves de reconnaître et d’apprendre les doubles. Il n’y a que dix faits numériques liés aux doubles. On peut faire appel à des trucs simples de mémorisation pour apprendre plusieurs doubles :
Double de 3 : un insecte a 3 pattes d’un côté et 3 pattes de l’autre (6).
Double de 4 : une araignée a 4 pattes d’un côté et 4 pattes de l’autre (8).
Double de 5 : les 5 doigts d’une main et les 5 doigts de l’autre (10).
Double de 6 : une boîte d’une douzaine d’œufs coupée en deux, 6 d’un côté et 6 de l’autre (12).
Double de 7 : sur le calendrier, il y a 7 jours dans une semaine et 14 jours dans deux semaines.
Double de 8 : il y a 8 crayons de couleur dans une rangée d’une boîte de crayons de couleur et 16 crayons dans deux rangées.
image La grille chiffrée s’intitule Utilisation des doubles. Dans le coin en haut à gauche, il y a le symbole plus. Les colonnes et les rangées se chiffrent respectivement de zéro à neuf. La rangée et la colonne zéro se chiffrent de zéro à neuf. La rangée et la colonne un se chiffrent d’un à dix. La rangée et la colonne deux se chiffrent de deux à onze. La rangée et la colonne trois se chiffrent de trois à douze. La rangée et la colonne quatre se chiffrent de quatre à treize. La rangée et la colonne cinq se chiffrent de cinq à 14. La rangée et la colonne six se chiffrent de six à 15. La rangée et la colonne sept se chiffrent de sept à 16. La rangée et la colonne huit se chiffrent de huit à 17. Et la rangée et la colonne neuf se chiffrent de neuf à 18.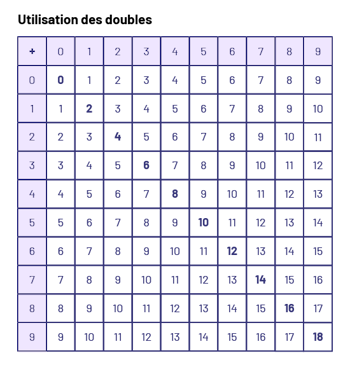
Les voisins des doubles ou les doubles plus 1 (5 + 4 peut être perçu comme 4 + 4, et 1 de plus)
Dans ces faits numériques de base, un des termes de l’addition est 1 de plus que l’autre terme. Les élèves peuvent apprendre à reconnaître que dans ces additions, la réponse est la même que le double du nombre le moins élevé plus \(\ 1 \ (5 + 4 = 4 + 4 + 1)\). Les élèves doivent bien maîtriser les doubles avant de pouvoir utiliser cette stratégie de manière efficace.
Commutativité (\(\ 1 + 2 = 2 + 1\))
Les élèves qui reconnaissent la propriété de commutativité de l’addition peuvent réduire de moitié la quantité de faits numériques qu’il leur faut apprendre. La représentation visuelle de faits comme \(\ 3 + 2\) et \(\ 2 + 3\) aide les élèves à saisir cette relation.
La soustraction comme opération inverse de l’addition pour les faits numériques de base ayant une somme allant jusqu’à 10
Les élèves, qui connaissent bien leurs additions et qui comprennent que la soustraction est l’opération inverse de l’addition, peuvent utiliser ces connaissances pour maîtriser les soustractions correspondantes (si \(\ 5 + 2 = 7\), il s’ensuit que \(\ 7 - 5 = 2\)). Prenons par exemple le problème suivant : « Julien a 6 billes dans son sac. Georges lui en donne d’autres. Julien a maintenant 10 billes. Combien de billes Georges a-t-il données à Julien? ». Placé devant ce problème, l’élève pense : « Quel nombre additionné à 6 donne 10? ». Ainsi, les faits d’addition qui lui sont familiers l’aident à trouver le terme inconnu dans la phrase mathématique.
« 1 de moins » et « 2 de moins »
Ces faits de soustraction ont un terme de 1 ou de 2 de moins que l’autre terme. Les élèves peuvent habituellement compter à rebours pour les faits numériques les plus faciles, comme n’importe quel nombre auquel on soustrait 0, 1 ou 2.
Regroupement par dizaines (\(\ 8 + 4 = 8 + 2 + 2 = 12\), \(\ 9 + 5 = 9 + 1 + 4 = 14\))
Dans ces faits numériques de base, l’un des termes est 8 ou 9. Selon le cas, les élèves ajoutent 1 ou 2 venant de l’autre terme pour obtenir 10, et lui ajoutent ce qui reste de cet autre terme. On devrait donner aux élèves de nombreuses occasions de travailler avec un cadre à dix cases afin que le regroupement devienne un automatisme.
Par exemple, dans une question comme \(\ 8 + 5\), les élèves peuvent obtenir 10 en additionnant 8 plus 2 (pris du 5), et additionner ensuite le 3 qui reste pour faire 13. Une fois que ces faits sont solidement acquis, il devient beaucoup plus facile pour les élèves de travailler avec de plus grands nombres, comme \(\ 18 + 5\). En sachant que \(\ 18 + 2\) égalent 20, il ne leur reste qu’à ajouter le 3 restant pour faire 23. (Cette propriété de l’addition se nomme l’associativité.)
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 14-20.
L’utilisation de la résolution de problèmes, des jeux ou d’enquêtes sont d’autres façons d’aider les élèves à apprendre à effectuer des calculs sur les nombres à plusieurs chiffres et à montrer l’utilité de telles opérations dans des situations concrètes.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 48.
L’estimation
Le but de l’estimation n’est pas d’arriver à une réponse exacte, mais à une approximation logique. Des questions comme « La réponse est-elle moins que 15? Plus que 10? » aident les élèves à reconnaître les possibilités et à évaluer la vraisemblance de leurs réponses. Quelques stratégies sont présentées afin que le personnel enseignant puisse aider les élèves à développer l’habileté à estimer. Il faut éviter d’enseigner ces stratégies comme des termes et des démarches à mémoriser ou à utiliser constamment. Le personnel enseignant peut s’en servir pour aider les élèves à mieux comprendre ce qu’elles et ils font et la raison pour laquelle elles et ils le font. Les stratégies peuvent être présentées aux élèves seulement lorsque l’occasion se présente. Il ne faut donc pas s’attendre à ce que les élèves utilisent ces stratégies, du moins pas avant les dernières années d’études du cycle primaire.
En 1re année, les élèves peuvent utiliser les stratégies d’estimation suivantes :
Regroupement
Le regroupement est utile lorsque les nombres sont plus faciles à calculer. Le regroupement permet d’effectuer une addition répétée.
\(\ 9 + 8 = \mathord{?}\) Chaque nombre est proche de 10. Si je regroupe les deux nombres, la réponse est environ 20.
Les nombres pratiques
La stratégie des nombres pratiques consiste à utiliser les nombres qui sont faciles à manier. Dans l’addition et la soustraction, les élèves cherchent les nombres dont la somme ou la différence est près de 10.
\(\ 2 + 4 + 2 + 6 = \mathord{?}\) Je regroupe 4 et 6, cela me donne 10. Ensuite, je regroupe 2 et 2 qui sont près de 5. Alors, la réponse est environ 15.
Bien des élèves ne saisissent pas l’importance et la pertinence de l’estimation. Elles et ils croient que l’estimation est une façon d’arriver à la réponse exacte, de sorte qu’il leur semble nécessaire de changer leur estimation après avoir effectué un calcul précis. En offrant chaque jour aux élèves de nombreuses occasions de s’exercer à estimer, le personnel enseignant peut les aider à améliorer cette habileté et ainsi à développer le sens de l’estimation et son utilité dans le quotidien.
Une estimation fournit aux élèves un guide leur permettant de déterminer si leur solution est vraisemblable.
Les élèves qui ont de multiples occasions de faire des estimations ont de meilleures chances de comprendre l’importance d’estimer et de raisonner de façon logique lorsqu’elles et ils travaillent avec les nombres.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 68-70.
Connaissance : stratégies liées au dénombrement
L’habileté des élèves à développer et à utiliser des stratégies liées au dénombrement, à la valeur de position et à la décomposition leur permet d’effectuer les opérations arithmétiques avec efficacité.
L’utilisation par les élèves de diverses stratégies liées au dénombrement (par exemple, décomposition, regroupement) leur permet d’effectuer les opérations arithmétiques de base avec efficacité et de mieux en comprendre le sens. Les élèves sont, par exemple, en mesure d’effectuer des calculs simples lorsqu’elles et ils réussissent à passer de « compter tout » à « compter à partir de » (par exemple, pour calculer \(\ 12 + 4\), au lieu de compter tous les jetons jusqu’à 12, puis d’en ajouter 4, l’élève commence à compter à partir de 12 en disant « 13, 14, 15, 16 »). Les élèves peuvent aussi apprendre à utiliser efficacement la décomposition et le regroupement des nombres pour additionner deux quantités. Ainsi, pour additionner 8 et 5, elles et ils peuvent décomposer 5 de manière à obtenir 2 et 3, regrouper ensuite 2 et 8 afin de former une dizaine et enfin additionner le 3 qui reste pour arriver à 13. Les stratégies liées à la décomposition en fonction des valeurs de position sont aussi fort utiles. Les élèves peuvent additionner en décomposant d’abord les deux nombres en dizaines et en unités. Les élèves peuvent aussi avoir recours à une stratégie liée aux doubles.
Lorsque les élèves connaissent bien toutes les façons de décomposer les nombres jusqu’à 10, elles et ils peuvent effectuer les additions et les soustractions de nombres inférieurs à 20 qui ne nécessitent pas de regroupements (par exemple, \(\ 10 + 4\), \(\ 11 + 6\) , \(\ 15 + 5\) ou \(\ 16 - 3\)). Ensuite, les élèves peuvent passer aux additions et aux soustractions de nombres inférieurs à 20 qui requièrent un regroupement (par exemple, \(\ 13 + 8\), \(\ 17 - 9\)).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 26-27.
