B2.3 Use mental math strategies, including estimation, to add and subtract whole numbers that add up to no more than 20, and explain the strategies used.
Skill: Using Mental Math Strategies
Problem solving using mental math is often a good way to encourage students to develop more efficient ways of doing calculations on paper. Teachers can encourage students to use mental math by presenting equations horizontally (14 + 6) rather than vertically:
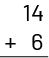
Students who take the time to look at the numbers and think about the best way to solve the equation before they start doing anything on paper are more likely to choose the most efficient way to solve the equation. For example, a moment of reflection before calculating (11 + 9) can help students realize that it is very easy to combine the 1 with 9 to make 10 and then add the remaining 10 to arrive at the answer, 20. When faced with a calculation, students often, but not always, use flexible strategies in their heads and make a few written notes, if necessary, to visualize their path.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 40-41.
The personal strategies developed by the student become their mental math strategies over time.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 38.
Therefore, it is important that teachers provide many experiences for students to become familiar with mental math strategies so that they develop flexibility with basic number facts about addition and subtraction.
When students see that the strategies they learned working with single-digit numbers can also be applied to multi-digit numbers, their understanding of multi-digit number operations improves. Therefore, they should be supported to make this connection.
One way to do this is to model the use of a known mental math strategy related to basic number facts and adapt it to include multi-digit numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 48.
Doing mental math means determining which representation of a number is most useful for performing a particular calculation. Using models, such as the ten frame, number line, and number grid to represent numbers and basic number facts can help students understand the meaning of basic operations and lessen their abstract nature.
The models help students make connections and thus better understand what the symbols represent in operations.
Teachers can help students connect their understanding of the problem first with manipulatives and then with symbols such as the =, +, and - signs, and then calculate mentally.
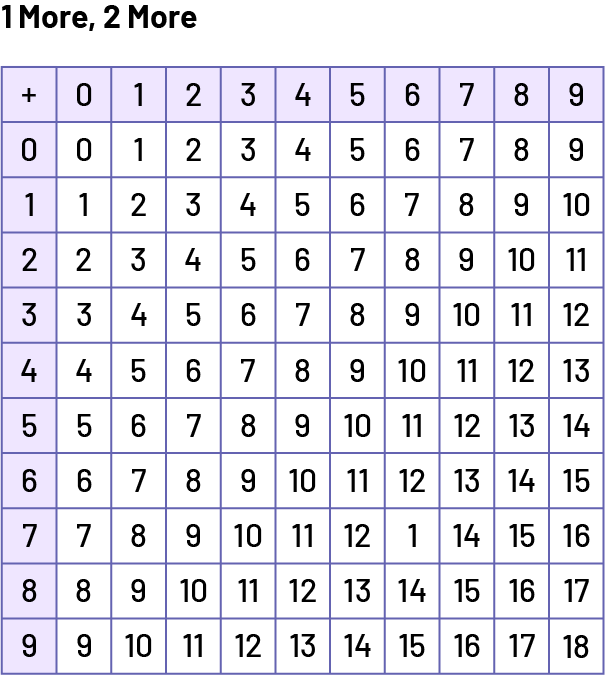
1 More and 2 More
In the basic number facts 5 + 1 = 6, 5 + 2 = 7, 7 + 1 = 8, 7 + 2 = 9, one of the terms in each addition is 1 or 2. The strategy is based on the assumption that students can easily remember the number that follows and the one that comes after.
Math Facts With 0 (1 + 0 = 1, 1 - 0 = 1)
In these basic number facts, 0 is one of the terms in each addition and subtraction. Students often overgeneralize by thinking that the answer to addition is necessarily larger and the answer to subtraction is necessarily smaller. Understanding the identity property in addition and subtraction can be reinforced through games using flashcards and numbered cubes.

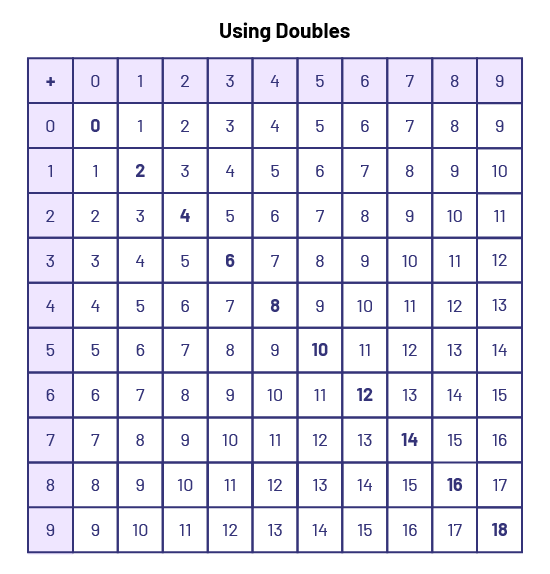
Use of Doubles
In these basic number facts, the first term and the second term (or both terms) are the same. It is beneficial for students to recognize and learn about doubles. There are only ten number facts related to doubles. Simple memorization tricks can be used to learn several doubles:
Double of 3: an insect has 3 legs on one side and 3 legs on the other (6).
Double of 4: a spider has 4 legs on one side and 4 legs on the other (8).
Double of 5: the 5 fingers of one hand and the 5 fingers of the other (10).
Double of 6: a box of a dozen eggs cut in half, 6 on one side and 6 on the other (12).
Double of 7: on the calendar, there are 7 days in a week and 14 days in two weeks.
Double of 8: There are 8 crayons in one row of a crayon box and 16 crayons in two rows.
Neighbours of Doubles or Doubles Plus 1 (5 + 4 can be seen as 4 + 4, and 1 more)
In these basic number facts, one term of the addition is 1 more than the other term. Students can learn to recognize that in these additions, the answer is the same as the double of the lower number plus (1) (5 + 4 = 4 + 4 + 1). Students need to be proficient with doubles before they can use this strategy effectively.
Commutative Property (1 + 2 = 2 + 1)
Students who recognize the commutative property of addition can cut the amount of number facts they need to learn in half. Visual representation of facts such as 3 + 2 and 2 + 3 helps students grasp this relationship.
Subtraction as the Inverse Operation of Addition for Basic Math Facts with a Sum up to 10
Students who know their addition well and understand that subtraction is the inverse operation of addition can use this knowledge to master the related subtractions (if 5 + 2 = 7, it follows that 7 - 5 = 2). For example, consider the following problem: "Julian has 6 marbles in his bag. George gives him some more. Julian now has 10 marbles. How many marbles did George give to Julian? Faced with this problem, the student thinks: "What number added to 6 gives 10? Thus, the addition facts with which he is familiar help him to find the unknown term in the number sentence.
1 Less and 2 Less
These subtraction facts have one term of 1 or 2 less than the other term. Students can usually count backwards for the easiest number facts, such as any number from which 0, 1, or 2 is subtracted.
Grouping by Tens (8 + 4 = 8 + 2 + 2 = 12), 9 + 5 = 9 + 1 + 4 = 14)
In these basic number facts, one of the terms is 8 or 9. As appropriate, students add 1 or 2 from the other term to get 10, and add what is left of that other term to it. Students should be given many opportunities to work with a ten frame so that grouping becomes automatic.
For example, in a question like 8 + 5, students can get 10 by adding 8 plus 2 (taken from 5), and then add the remaining 3 to make 13. Once these facts are firmly established, it becomes much easier for students to work with larger numbers, such as 18 + 5. Knowing that 18 + 2 equals 20, they need only add the remaining 3 to make 23. (This property of addition is called the associative property.)
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 14-20.
The use of problem solving, games, or investigations are other ways to help students learn to perform calculations on multi-digit numbers and to demonstrate the usefulness of such operations in real-world situations.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 48.
Estimation
The goal of estimation is not to arrive at an exact answer, but a logical approximation. Questions such as "Is the answer less than 15? More than 10?" help students recognize possibilities and assess the reasonableness of their answers. Some strategies are presented so that teachers can help students develop the skill of estimating. These strategies should not be taught as terms and procedures to be memorized or used constantly. Teachers can use them to help students better understand what they are doing and why they are doing it. Strategies can be introduced to students only when the opportunity arises. Therefore, students should not be expected to use these strategies, at least not until the later grades.
Many students do not understand the importance and relevance of estimation. They believe that estimating is a way of arriving at the correct answer, so they find it necessary to change their estimation after making an accurate calculation. By providing students with many opportunities to practice estimating each day, teachers can help them improve this skill and thus develop a sense of estimation and its usefulness in everyday life.
An estimation provides students with a guide to determine if their solution is reasonable.
Students who have multiple opportunities to estimate are more likely to understand the importance of estimating and logical reasoning when working with numbers.
In Grade 1, students may use the following estimation strategies:
Grouping
Grouping is useful when numbers are easier to calculate. Grouping allows for repeated addition.
Each number is close to 10.
When 9 + 8 = ?, the answer is about 20.
Friendly Numbers
The friendly number strategy is to use numbers that are easy to handle. In addition and subtraction, students look for numbers whose sum or difference is near 10.
I put 4 and 6 together, which gives me 10. Then I put 2 and 2 together, which is close to 5. So the answer is about 15.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 68-70.
Knowledge: Counting Strategies
Using a variety of counting strategies (for example, decomposition, regrouping) supports students in performing basic arithmetic operations effectively and with understanding. For example, students are able to perform simple calculations when they successfully move from "counting all" to "counting up" (for example, to calculate 12 + 4, instead of counting all the counters up to 12 and then adding 4, the student begins to count up from 12 by saying "13, 14, 15, 16"). Students can also learn to effectively use number decomposition and grouping to add two quantities. For example, to add 8 and 5, they can decompose 5 to get 2 and 3, then group 2 and 8 together to form a ten, and finally add the remaining 3 to get 13. Strategies related to decomposing by place values are also very useful. For example, students can add by first decomposing two numbers into tens and ones. Students can also use a strategy related to doubles.
Once students are familiar with all the ways to decompose numbers to 10, they can perform addition and subtraction of numbers less than 20 that do not require regrouping (for example, 10 + 4, 11 + 6, 15 + 5, or 16 - 3). Next, students can move on to addition and subtraction of numbers less than 20 that require regrouping (for example, 13 + 8, 17 - 9).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 26-30.
