B1. Sens du nombre
Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne.
Situation d’apprentissage 1 : les pansements (dénombrement)
Durée totale : 2 h 10 min
| Attente | Contenus d'apprentissage |
| Nombres B1. Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire et représenter les nombres naturels de 0 jusqu’à 50 et décrire de quelles façons ils sont utilisés dans la vie quotidienne. B1.3 Comparer et ordonner les nombres naturels jusqu’à 50, dans divers contextes. B1.4 Estimer le nombre d’objets dans des ensembles qui comprennent jusqu’à 50 objets et vérifier son estimation en utilisant des stratégies de dénombrement. B1.5 Compter jusqu’à 50 par intervalles de 1, 2, 5 et 10, à l’aide d’une variété d’outils et de stratégies. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :
- d’utiliser les nombres dans des contextes signifiants pour décrire des situations;
- de compter par 2, par 5 et par 10;
- de compter à partir de n’importe quel nombre;
- de comparer, par correspondance de un à un, les objets de deux ensembles;
- de classer et d’ordonner des éléments pour résoudre un problème;
- d’estimer un nombre d’objets et d’en vérifier l’exactitude en comptant.
| Contexte pédagogique | Préalables |
|---|---|
| Dans les premières années d’études, le dénombrement est à la fois une habileté et une stratégie qui permet à l’élève de résoudre des problèmes. L’élève de 1re année continue à apprendre le nom des nombres en comptant jusqu’à 50. L’élève commence aussi à compter par intervalles de 2, de 5 et de 10. Ces façons de compter lui permettent de reconnaître des régularités et lui fournissent une stratégie intéressante pour dénombrer une grande quantité d’objets. L’habileté à compter dans l’ordre ascendant ou descendant à partir de n’importe quel nombre devient une stratégie importante pour résoudre certains problèmes. Il faut cependant tenir compte du fait que la plupart des élèves trouvent plus difficile de compter dans l’ordre descendant que dans l’ordre ascendant. En outre, des élèves hésitent ou ont du mal à compter en passant d’une dizaine à l’autre, par exemple en passant de 29 à 30, ou éprouvent des difficultés à nommer certains nombres entre 11 et 16. | Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Matériel
Activité principale
- annexe 1D.1 (Les pansements) (une copie par élève)
- annexe 1D.2 (Silhouette du personnage) (une copie par élève)
- annexe 1D.3 (Résolution de problème : les pansements) (une copie par élève)
- annexe 1D.4 (Combien y en a-t-il?) (une copie par élève)
- grande feuille de papier
- papier d’emballage
- marqueurs (un rouge et un vert)
- pansements adhésifs ou petites bandes de ruban-cache (au moins 35 par équipe)
- boîte contenant 35 pansements adhésifs (1)
- objets (par exemple, jetons, cubes emboîtables)
Activité supplémentaire 1
- ficelle
- perles
- cubes emboîtables
- céréales rondes
Activité supplémentaire 2
- bâtonnets de bois (10 par équipe)
Vocabulaire mathématique
nom des nombres de 1 à 60.
Avant l’apprentissage (mise en train)
Durée : environ 40 min
Tracer à l’avance, à partir de l’annexe 1D.2 (Silhouette du personnage) ou à main levée, une grande silhouette du personnage sur du papier d’emballage. La découper et la suspendre de façon que les élèves puissent la voir. Placer la boîte contenant 35 pansements près de la silhouette.
Écrire à l’avance le poème Pansements de Shel Silverstein (annexe 1D.1) sur une grande feuille de papier et l’afficher ou le projeter sur le TBI.
Lire le poème avec les élèves.
Inviter des élèves à chercher les nombres dans le poème et à les encercler à l’aide d’un marqueur rouge.
Demander ensuite à d’autres élèves de trouver les noms des parties du corps et de les encercler à l’aide d’un marqueur vert.
Présenter la boîte de pansements et demander aux élèves le nombre de pansements qu’elle contient.
Pendant l’apprentissage (exploration)
Durée : environ 50 min
Relire le poème à haute voix. Inviter une ou un élève à venir indiquer du doigt, au fur et à mesure, les parties du corps sur la grande silhouette et demander aux autres de les indiquer sur leur corps. Cet exercice les aidera à réaliser qu’il y a beaucoup de pansements sur le personnage.
Former des équipes de deux.
Remettre une copie des annexes 1D.2 et 1D.3 à chaque groupe et mettre à leur disposition du matériel de manipulation tel que des jetons, un tableau de dénombrement, des pansements, du ruban-cache.
Présenter le problème « Est-ce qu’il y a plus de pansements sur le personnage ou dans la boîte? Comment le sais-tu? ».
Inciter les élèves à discuter avec une ou un partenaire de leur stratégie pour résoudre le problème. Cette discussion leur permet de réaliser qu’il y a plus d’une façon de trouver la solution. Les partenaires qui ont proposé des stratégies différentes doivent ensuite décider laquelle choisir.
Circuler pendant que les élèves travaillent et poser des questions pour stimuler la réflexion telles que :
- Comment vas-tu dénombrer les pansements sur le personnage?
- Comment vas-tu faire pour déterminer l’endroit où il y en a le plus?
- Comment vas-tu faire pour déterminer l’endroit où il y en a le moins?
- Quelle stratégie as-tu utilisée pour résoudre le problème?
Afficher les solutions des élèves.
Après l’apprentissage (objectivation/transfert des connaissances)
Durée : environ 40 min
Demander à chaque équipe de faire part au groupe-classe de leur stratégie pour résoudre le problème.
Dénombrer les pansements, avec les élèves, en les plaçant sur la grande silhouette afin de vérifier si leurs réponses sont justes.
Poser aux élèves les questions suivantes :
- Qu’est-ce qui rendait ce problème difficile à résoudre?
- De quelle façon avez-vous déterminé le nombre de pansements sur le personnage?
- Comment avez-vous fait pour déterminer s’il y avait plus de pansements sur le personnage ou dans la boîte?
Faire ressortir :
- qu’il y a plusieurs façons de dénombrer les pansements (par exemple, en comptant par 1 ou par intervalles de 2, de 5 et de 10).
- que le regroupement permet de dénombrer plus facilement une grande quantité d’objets.
- que la correspondance de un à un permet de résoudre le problème sans dénombrer.
Exemples de critères d’évaluation
L’élève :
- explique le problème en ses propres mots;
- cherche de nouvelles stratégies;
- choisit du matériel de manipulation approprié;
- regroupe les objets pour faciliter le dénombrement;
- explique clairement la stratégie utilisée.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
Pour faciliter la tâche
Remettre aux élèves une silhouette sur laquelle les pansements ont été collés et leur proposer diverses stratégies à utiliser pour dénombrer les pansements (par exemple, faire un X sur chaque pansement en comptant, décoller les pansements et faire des groupes de 1, de 2 ou de 5 avant de les dénombrer).Suivi à la maison
Combien y en a-t-il?
À la maison, l’élève peut dénombrer divers objets tels que les portes, les fenêtres, les cuillères, les fourchettes, les lampes, les horloges.
Remettre une copie de l’annexe 1D.4 (Combien y en a-t-il?) à chaque élève pour qu’elle ou il puisse réaliser l’activité avec une ou un membre de sa famille.
Activité supplémentaire 1
Colliers compteurs
Attribuer un nombre différent à chaque élève selon sa compréhension du sens du nombre. Leur demander de fabriquer un collier compteur (collier de perles, de céréales ou de cubes emboîtables) pour représenter le nombre.
Accroître la difficulté en leur demandant de faire des colliers montrant le dénombrement par intervalles de 2, de 5 ou de 10; par exemple, les élèves peuvent alterner des couleurs ou des matériaux, ou encore insérer des formes découpées ou autres objets entre chaque groupe de 2, de 5 ou de 10.
Leur demander d’échanger les colliers et de dénombrer les éléments qui les composent.
Conserver les colliers; ils peuvent servir de matériel concret pour permettre aux élèves de s’exercer ou aider les élèves à dénombrer.
Activité supplémentaire 2
Allons nous promener
Demander aux élèves d’estimer le nombre de pas à faire pour traverser la classe d’un bout à l’autre.
Leur demander de parcourir la distance tout en comptant le nombre de pas nécessaires pour vérifier leur réponse.
Former des équipes de deux et leur demander de trouver une stratégie pour déterminer le nombre de pas à faire pour se rendre de la classe au secrétariat ou au gymnase de l’école.
Demander à chaque équipe de mettre sa stratégie à l’essai pour trouver la réponse.
Offrir aux équipes qui ne peuvent trouver de stratégie d’utiliser des bâtonnets pour représenter 10 pas. Une ou un élève compte tandis que l’autre tient les bâtonnets. Chaque fois que l’élève qui compte arrive à 10, l’autre lui donne un bâtonnet. À la fin, les élèves peuvent dénombrer chaque groupe de 10 (représenté par un bâtonnet) pour déterminer le nombre total de pas.
Inviter chaque équipe à dire le nombre de pas entre les deux endroits et à expliquer la stratégie utilisée pour dénombrer les pas sans se tromper.
Noter les réponses de chaque équipe au tableau aux fins de comparaison et discuter des raisons pour lesquelles chacune n’a pas obtenu exactement le même nombre de pas.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 85-90.
Situation d’apprentissage 2 : la grosse prise (quantité)
Durée totale : 2 heures
| Attente | Contenus d'apprentissage |
| Nombres B1. Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire et représenter les nombres naturels de 0 jusqu’à 50 et décrire de quelles façons ils sont utilisés dans la vie quotidienne. B1.2 Composer et décomposer les nombres naturels de 0 jusqu’à 50, à l’aide d’une variété d’outils et de stratégies, dans divers contextes. B1.4 Estimer le nombre d’objets dans des ensembles qui comprennent jusqu’à 50 objets et vérifier son estimation en utilisant des stratégies de dénombrement. B1.5 Compter jusqu’à 50 par intervalles de 1, de 2, de 5 et de 10, à l’aide d’une variété d’outils et de stratégies. |
Intention pédagogique
Cette situation aide l’élève :
- à estimer des quantités d’objets à partir d’un point de repère;
- à reconnaître diverses représentations visuelles des nombres à partir d’assiettes à pois.
| Contexte pédagogique | Préalables |
|---|---|
| L’élève doit développer un sens de la quantité ou du nombre d’objets contenus dans divers ensembles. L’estimation de la quantité devrait être acquise le plus tôt possible. Au cours des premières années d’études, l’élève réussit mieux à estimer les quantités lorsqu’on lui donne un choix fixe, par exemple : « Y a-t-il environ 5 ou 10 objets? », « Y en a-t-il environ 20 ou 30? » Les questions de ce genre amènent l’élève, qui n’a pas développé un bon sens du nombre, à faire des estimations plus justes. L’élève apprend aussi à utiliser un point de repère pour améliorer ses habiletés. Par exemple, en visualisant d’abord l’espace qu’occupent 20 billes dans un pot, elle ou il peut plus facilement estimer une quantité plus grande ou plus petite de billes dans ce pot. | Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Matériel
Activité principale
- annexe 1Q.1 (Les nombres cibles) (une copie par élève)
- annexe 1Q.2 (Chez moi) (une copie par élève)
- récipients (un par équipe de quatre)
- petits objets (centicubes [petits cubes de 1 cm3], cubes, jetons bicolores, haricots secs ou boutons)
- feuille grand format
Activité supplémentaire 1
- annexe 1Q.3 (Un problème juteux) (une copie par élève)
- feuille grand format
- boîtes de jus vides (jus préféré de chaque élève)
- matériel de manipulation (cubes ou jetons de la même couleur que les diverses sortes de jus)
Vocabulaire mathématique
plus, moins, autant
Avant l’apprentissage (mise en train)
Durée : environ 40 min
Montrer aux élèves un récipient rempli de petits objets identiques (cubes, centicubes, jetons, haricots secs ou boutons).
Indiquer aux élèves que vous allez essayer de prendre 22 objets dans votre main et inscrire 22 sur une grande feuille de papier.
Prendre une poignée d’objets et les compter à voix haute avec les élèves. Inscrire, sur la feuille, le nombre réel d’objets saisis afin d’avoir un point de repère pour se rapprocher le plus près possible du nombre cible lors de la prochaine pige.
Poser aux élèves les questions suivantes :
- Combien d’objets est-ce que je devais prendre?
- Est-ce que j’en ai pris plus ou moins?
- Est-ce que j’ai atteint le nombre cible?
- Est-ce que j’en ai pris trop ou pas assez?
Répéter l’activité en essayant de se rapprocher du nombre cible.
Demander de nouveau aux élèves si le nombre d’objets retirés du récipient est trop ou pas assez grand.
Former des équipes de quatre et placer un récipient rempli de petits objets identiques sur chaque table.
Demander à chaque élève de prendre une poignée de 18 objets dans le récipient.
Faire dénombrer les objets pour vérifier le nombre d’élèves :
- qui ont atteint le nombre cible;
- qui sont à deux objets du nombre cible;
- qui sont à cinq objets du nombre cible.
Répéter l’activité, mais en donnant un autre nombre d’objets à prendre dans le récipient.
Pendant l’apprentissage (exploration)
Durée : environ 50 min
Remettre une copie de l’annexe 1Q.1 à chaque élève.
Demander aux élèves :
- de se choisir un nombre cible entre 10 et 25 et de l’inscrire dans le cercle sur la fiche;
- d’essayer de prendre dans le récipient le nombre d’objets inscrit sur la fiche;
- de dénombrer individuellement les objets retirés du récipient afin d’avoir un point de repère lors du prochain essai;
- d’inscrire le résultat de ce premier essai à l’endroit approprié sur la fiche;
- d’indiquer ensuite si ce nombre est supérieur ou inférieur au nombre cible;
- de faire de nouveaux essais en essayant de se rapprocher davantage du nombre choisi.
Poursuivre l’activité jusqu’à ce que les élèves aient essayé quatre nombres cibles différents.
Circuler dans la salle de classe pendant que les élèves travaillent. Observer leur façon de procéder et poser des questions telles que :
- Comment as-tu fait pour savoir que tu avais pris trop ou pas assez d’objets?
- Est-ce que tu étais plus près du nombre cible à ton deuxième essai?
- Pourquoi étais-tu plus près du nombre cible la deuxième fois?
- Après avoir joué plusieurs fois, était-il plus facile de se rapprocher du nombre exact d’objets?
Après l’apprentissage (objectivation/transfert des connaissances)
Durée : environ 30 min
Rassembler les élèves et leur poser les questions suivantes :
- Quel a été ton plus grand nombre cible?
- Quel a été ton plus petit nombre cible?
- Comment as-tu fait pour savoir que tu avais pris trop ou pas assez d’objets?
- Est-ce que tu étais plus près du nombre cible au deuxième essai?
- Pourquoi étais-tu plus près du nombre cible la deuxième fois?
- Après avoir joué plusieurs fois, était-il plus facile dès le premier essai de se rapprocher du nombre exact d’objets? Pourquoi?
Faire remarquer aux élèves que le nombre d’objets retirés lors du premier essai a servi de point de repère pour les aider à se rapprocher le plus près possible du nombre cible au deuxième essai.
Exemples de critères d’évaluation
L’élève :
- améliore la précision de sa prise au deuxième essai;
- fait des estimations de plus en plus justes;
- détermine si elle ou il a pris plus, moins ou autant d’objets que le nombre cible;
- utilise les mots plus, moins et autant.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|
|
Suivi à la maison
Chez moi
À la maison, l’élève peut indiquer des objets qui se trouvent en petite quantité, en grande quantité ou en quantité fixe.
Remettre une copie de l’annexe 1Q.2 à chaque élève pour qu’elle ou il puisse réaliser l’activité.
Activité supplémentaire 1
Un problème juteux
Faire un sondage auprès des élèves pour connaître leur jus préféré parmi les suivants : jus de pomme, jus d’orange ou jus de raisin.
Utiliser des boîtes de jus vides pour représenter les données recueillies lors du sondage dans un diagramme concret ou dans un diagramme à pictogrammes.
Remettre une copie de l’annexe 1Q.3 à chaque élève.
Présenter le problème suivant :
Nous préparons une fête pour célébrer la nouvelle saison. Nous voulons que chaque élève reçoive au moins une boîte de son jus préféré. Combien de paquets de chaque sorte de jus devons-nous acheter?
Examiner l’annexe 1Q.3 avec les élèves et leur faire découvrir que les jus se vendent en paquets seulement.
Poser aux élèves les questions suivantes :
- Combien de boîtes de jus de pomme y a-t-il dans un paquet?
- Combien de boîtes de jus d’orange y a-t-il dans un paquet?
- Combien de boîtes de jus de raisin y a-t-il dans un paquet?
Inciter les élèves à utiliser des objets ou à faire des dessins pour résoudre le problème.
Préciser que les élèves doivent indiquer, sur leur feuille de travail, la stratégie utilisée pour résoudre le problème.
Faire une mise en commun pour que les élèves puissent expliquer la façon dont a été résolu le problème.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 101-105.
Situation d’apprentissage 3 : le jeu des échanges (représentation)
Durée totale : 2 h 30 min
| Attente | Contenus d'apprentissage |
| Nombres B1. Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire et représenter les nombres naturels de 0 jusqu’à 50 et décrire de quelles façons ils sont utilisés dans la vie quotidienne. B1.2 Composer et décomposer les nombres naturels de 0 jusqu’à 50 à l’aide d’une variété d’outils et de stratégies, dans divers contextes B1.3 Comparer et ordonner les nombres naturels jusqu’à 50 dans divers contextes. B1.4 Estimer le nombre d’objets dans des ensembles qui comprennent jusqu’à 50 objets et vérifier son estimation en utilisant des stratégies de dénombrement. B1.5 Compter jusqu’à 50 par intervalles de 1, de 2, de 5 et de 10 à l’aide d’une variété d’outils et de stratégies. |
Intention pédagogique
Le but de cette situation est d’aider l’élève :
- à illustrer différentes façons de représenter les nombres à l’aide de matériel concret;
- à déterminer le nombre de dizaines et d’unités d’un ensemble;
- à déterminer la valeur d’un chiffre selon sa position dans un nombre;
- à utiliser les mots dizaine et unité pour décrire la représentation des nombres.
| Contexte pédagogique | Préalables |
|---|---|
| En 1re année, l’élève continue à découvrir les nombreuses façons de représenter les nombres. Elle ou il sait que les nombres représentent des quantités et qu’ils peuvent être représentés par des objets. Les diverses représentations nous renseignent surtout sur ce qu’est le nombre, sur ses caractéristiques internes et ses décompositions. En 1re année, l’élève s’initie au concept de valeur de position et à son rôle dans la représentation des nombres. Bien que l’élève de 1re année soit capable de compter jusqu’à 50 et réussisse de mieux en mieux à représenter les nombres à l’aide de matériel concret, les ensembles lui apparaissent encore comme des groupes d’éléments individuels; par exemple, l’élève de 1re année à qui l’on demande de représenter le nombre 23 à l’aide d’objets montrera peut-être trois jetons pour représenter les trois unités et uniquement deux jetons pour représenter les 20 autres. Elle ou il a souvent de la difficulté à saisir l’idée qu’un groupe de 10 éléments peut être représenté par le chiffre 1 dans un nombre comme 11. | Dans cette situation d’apprentissage, l’élève doit pouvoir :
L’élève doit également avoir été initiée ou initié au concept de conservation du nombre. |
Matériel
Activité principale
- annexe 1Rep.1 (Tapis de valeur de position) (une copie par élève)
- feuille grand format
- marqueur
- récipients renfermant 35 jetons (un par élève)
- feuilles de papier
- trousse de valeur de position :
- bâtonnets de bois, cubes emboîtables ou centicubes (60 par élève)*;
- cure-pipes (4 par élève);
- sacs en plastique réutilisables (un par élève)
- dés (un par équipe)
- cure-dents (36)
* Préférer les bâtonnets, les cubes emboîtables ou les centicubes au matériel de base 10 qui est plus adapté à un groupe d’âge plus avancé pour représenter la valeur de position.
Activité supplémentaire 1
- annexe 1Rep.2 (C’est dans le sac!) (une copie par équipe de deux)
- annexe 1Rep.3 (Contenu des sacs)
- marqueur
- sacs en plastique réutilisables (30)
- petits objets
Activité supplémentaire 2
- annexe 1Rep.4 (Grille de nombres de 1 à 60) (une copie par élève)
- jetons
Activité supplémentaire 3
- grille de nombres munie de pochettes transparentes
- cartes de nombre de 1 à 50 pour la grille
Vocabulaire mathématique
dizaines, unités, échanger, regrouper, valeur de position
Avant l’apprentissage (mise en train)
Durée : environ 40 min
Avant l’entrée des élèves :
- dessiner 35 binettes sur une feuille grand format en les disposant de manière à ne pas créer de rangées ou de colonnes visibles et la plastifier ou projeter 35 binettes en les disposant de manière à ne pas créer de rangées ou de colonnes visibles;

- déposer un récipient renfermant 35 jetons, une feuille de papier et un crayon sur le pupitre de chaque élève.
Attirer l’attention des élèves sur la feuille grand format et leur demander d’estimer le nombre de binettes. Elles et ils essaieront peut-être de les dénombrer en les montrant du doigt, mais ce sera difficile.
Écrire toutes les estimations au tableau.
Demander aux élèves de réfléchir aux différentes manières de s’y prendre pour les dénombrer; par exemple, compter par groupes de 2, de 5 et de 10.
Dire aux élèves que, dans le récipient déposé sur leur pupitre, il y a le même nombre de jetons que de binettes sur la feuille grand format.
Proposer aux élèves d’utiliser les jetons pour représenter les différentes façons de s’y prendre pour dénombrer les binettes; par exemple, en faisant des groupes de 2, de 5 et de 10.
Après quelques minutes, leur poser la question suivante : « Quelles façons avez-vous trouvées pour dénombrer les jetons? ». Demander à l’élève qui suggère un regroupement de 2, de 5 ou de 10 de l’expliquer.
Regrouper les élèves autour de la feuille grand format, puis leur demander de nommer la meilleure façon, parmi celles qui ont été présentées, de dénombrer les binettes et d’expliquer leur réponse.

Entourer des groupes de 10 binettes.
Faire dénombrer les groupes de 10 et les binettes qui restent.
Écrire au tableau :
\(\ 3 \ \mathord{groupes\ de\ 10\ binettes}\)
\(= 10 + 10 + 10\)
\(= 30\)
\(\ + 5 \ \mathord{binettes}\)
\(\ + 1 + 1 + 1 + 1 + 1\)
\(\ + 5\)
Poser aux élèves la question suivante : Combien y a-t-il de binettes en tout? Écrire « = 35 ».
Faire remarquer aux élèves que 3 groupes de 10 et 5 unités correspondent au nombre 35.
Souligner qu’on appelle les groupes de 10 des dizaines et les binettes seules, des unités.
Poser aux élèves la question suivante : Comment peut-on se rappeler les mots dizaine et unité?
Pendant l’apprentissage (exploration)
Durée : environ 60 min
1re partie
Indiquer aux élèves qu’une trousse de valeur de position doit être préparée. Pour ce faire, remettre à chaque élève 50 bâtonnets, 3 cure-pipes et un sac en plastique.
Demander aux élèves de faire 3 paquets de 10 bâtonnets et d’attacher chaque paquet à l’aide d’un cure-pipe, puis de garder les 20 bâtonnets qui restent non attachés.
Poser aux élèves les questions suivantes :
- Combien de paquets de 10 bâtonnets avez-vous?
- Combien de bâtonnets non attachés avez-vous?
- Quel nom donne-t-on aux paquets de bâtonnets groupés?
- Pourquoi appelle-t-on les paquets des dizaines?
- Quel nom donne-t-on aux bâtonnets non attachés?
- Pourquoi les appelle-t-on des unités?
- Combien de bâtonnets y a-t-il en tout?
Écrire au tableau :
\(\ 3 \ \mathord{dizaines}\)
\(= 10 + 10 + 10\)
\(= \ \ \ \ \ \ \ 30\)
\(= \ \ \ \ \ \ \ 50\)
\(\ + 20 \ \mathord{unités}\)
\(\ + \ \ \ \ 20\)
\(\ + \ \ \ \ 20\)
Remettre à chaque élève une copie de l’annexe 1Rep.1 et expliquer que le tapis de valeur de position sert à représenter les nombres selon les dizaines et les unités.
Projeter un tapis de valeur de position et montrer la façon de représenter le nombre 16 à l’aide de cure-dents : un paquet de 10 cure-dents dans la colonne des dizaines et 6 cure-dents dans celle des unités.
Demander aux élèves de se servir de leur trousse pour représenter le nombre 25 sur leur tapis.
Inviter une ou un élève à dire ce qu’a fait l’élève et l’illustrer à l’écran à l’aide de cure-dents.
Demander aux élèves de trouver une deuxième façon de représenter 25, puis une troisième, et illustrer leurs suggestions à l’écran.
Souligner que 25 unités ou 2 paquets de 10 et 5 unités ou que un paquet de 10 et 15 unités sont diverses représentations de 25.
Poursuivre l’activité en demandant aux élèves de représenter les nombres suivants : 12, 7, 18, 20 et 36.
Faire illustrer chaque nombre à l’aide de cure-dents et poser aux élèves les questions ci-dessous pour chacun :
- Combien de dizaines avez-vous utilisées pour illustrer ce nombre?
- Combien d’unités avez-vous utilisées pour illustrer ce nombre?
- Y a-t-il d’autres façons de représenter ce nombre?
Note : Il est important de varier le matériel de manipulation dans la trousse, comme les cubes emboîtables ou le cadre à 10 cases.
2e partie
Apprendre aux élèves à jouer au Jeu des échanges, qui se joue à deux, à trois ou à quatre.
S’assurer que chaque élève a une trousse de valeur de position et une copie du tapis de valeur de position (annexe 1Rep.1).
Expliquer aux élèves qu’une des règles du jeu des échanges est que l’on ne peut jamais avoir plus de 9 bâtonnets dans la colonne des unités. Lorsqu’il y a plus de 9 unités dans la colonne, il faut échanger 10 unités contre un paquet de 10 et mettre tous les paquets de 10 dans la colonne des dizaines.
Demander aux élèves d’expliquer la raison pour laquelle il faut placer les paquets de 10 dans la colonne des dizaines.
Modeler le jeu et dire aux élèves de mettre le même nombre de bâtonnets sur leur propre tapis de valeur de position.
- Lancer le dé. Si le 6 sort, mettre 6 bâtonnets dans la colonne des unités.
- Lancer le dé de nouveau. Si le 2 sort, ajouter 2 bâtonnets dans la colonne des unités et demander aux élèves de dire le nombre d’unités qu’il y a maintenant (8).
- Lancer le dé de nouveau. Si le 4 sort, ajouter 4 bâtonnets dans la colonne des unités et demander aux élèves de dire le nombre d’unités qu’il y a maintenant (12).
Dire : « Oh! Quelle est la règle? »
Laisser les élèves s’apercevoir qu’il faut échanger les 10 bâtonnets contre un paquet de 10 et le mettre dans la colonne des dizaines.
Poser aux élèves les questions suivantes :
- Qu’avez-vous sur votre tapis? (1 dizaine et 2 unités)
- Combien cela fait-il de bâtonnets? (12)
Rappeler que ce qui a changé, ce n’est pas le nombre, mais sa représentation seulement.
Continuer à jouer jusqu’à ce que le nombre atteigne ou dépasse 30 et interroger les élèves après chaque lancer du dé.
Faire jouer les élèves en équipes. Elles et ils lancent le dé à tour de rôle, ajoutent des bâtonnets sur leur tapis et, le moment venu, échangent 10 unités contre une dizaine. L’élève qui est la première ou le premier à obtenir 3 dizaines (30) gagne.
Jouer à ce jeu souvent pendant l’année. Ranger les tapis, les trousses de valeur de position et les dés dans un bac pour que les élèves aient accès au matériel pendant les moments d’activité libre.
Variante
Modifier les règles du jeu pour jouer de 30 à 0 plus tard dans l’année. Pour ce faire, les élèves mettent trois paquets de 10 dans la colonne des dizaines comme point de départ et défont des paquets pour soustraire les nombres qu’indique le dé. Cette activité les initie graduellement aux concepts de décomposition et de regroupement dans les additions et les soustractions des nombres à deux chiffres.
Après l’apprentissage (objectivation/transfert des connaissances)
Durée : environ 50 min
Se joindre à une équipe de quatre pendant que les autres poursuivent leur jeu.
Leur demander de représenter le nombre 27 sans leur tapis de valeur de position.
Accorder une grande place à la discussion pendant le travail pour que chaque élève puisse décrire ce qui est fait dans ses propres mots.
Poser à l’élève quelques questions lorsque les explications ne sont pas claires :
- Comment as-tu représenté le nombre 27?
- Y a-t-il d’autres façons de représenter ce nombre? Lesquelles? (L’élève peut dire que 27 correspond à 2 dizaines et à 7 unités, à une dizaine et à 17 unités ou à 27 unités.)
- Combien de groupes de 10 as-tu faits?
- Combien d’unités as-tu placées sur le tapis?
- Où as-tu placé les dizaines?
- Où as-tu placé les unités?
- Après avoir fait des paquets de 10 unités, combien d’unités reste-t-il?
- Pourquoi fais-tu un paquet de 10 maintenant?
- Que représente le chiffre 2 dans le nombre 27?
- Que représente le chiffre 7 dans le nombre 27?
- Combien de dizaines y a-t-il dans le nombre 27?
- Combien y a-t-il d’unités en tout dans le nombre 27?
- Quelle représentation correspond le mieux à la façon d’écrire les nombres? (2 paquets de 10 et 7 unités)
Mettre l’accent sur le fait que 2 dizaines et 7 unités ont la même valeur que 27 unités. La représentation peut être différente, mais la quantité demeure la même.
Circuler parmi les élèves et les observer pendant les échanges, et consigner, dans un dossier anecdotique, les observations sur leurs habiletés à représenter les nombres, à regrouper les unités en dizaines et à expliquer les stratégies.
Exemples de critères d’évaluation
L’élève :
- représente les nombres de manière exacte;
- représente un nombre de différentes façons;
- explique qu’une quantité ne change pas, même si sa représentation est différente;
- utilise convenablement les mots dizaine et unité;
- utilise des mots tels que trop, regrouper, paquet et échanger pour expliquer ce que fait l’élève.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
Pour faciliter la tâche
- travailler plus longtemps à représenter des nombres sur le tapis de valeur de position avant de passer au jeu proprement dit;
- commencer par de petits nombres et progresser lentement vers de plus grands nombres.
Suivi à la maison
Jeu des échanges
À la maison, l’élève peut enseigner les règles du jeu des échanges aux membres de sa famille et jouer avec eux.
S’assurer que l’élève connaît bien les règles du jeu avant de lui laisser apporter une trousse de valeur de position à la maison.
Activité supplémentaire 1
Création d’un centre de valeur de position
Numéroter 30 sacs en plastique à l’aide de ruban-cache et d’un marqueur.
Grouper les élèves en équipes de deux et remettre à chaque équipe une copie de l’annexe 1Rep.2.
Remettre de un à quatre sacs à chaque équipe.
Demander aux élèves de mettre une quantité différente d’objets dans chacun des sacs; par exemple, sac no 2 : 26 billes; sac no 27 : 54 jetons.
Leur préciser :
- d’écrire le numéro du sac et le nombre d’objets contenus dans chacun sur leur fiche de réponses (annexe 1Rep.2);
- d’indiquer les différents groupes de dizaines et d’unités qui peuvent représenter le nombre d’objets dans le sac.
Exemple :
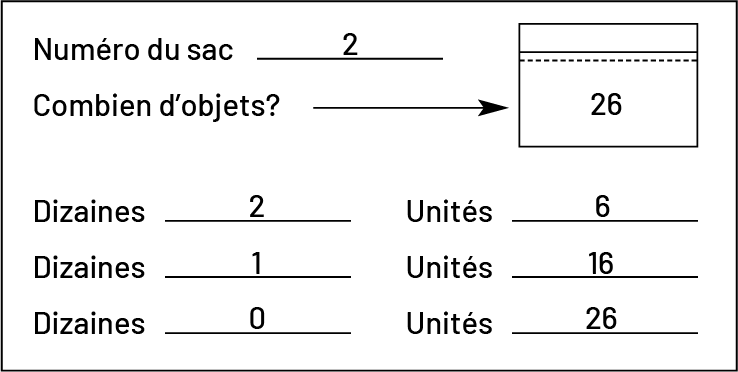
Dresser une liste du contenu de tous les sacs (quantité et nom des objets) à l’aide de l’annexe 1Rep.3.
Mettre des copies de l’annexe 1Rep. 2 ainsi que les sacs dans un centre d’apprentissage pour que les élèves puissent les utiliser pendant les temps d’activité libre.
Demander aux élèves de choisir différents sacs et de remplir une nouvelle feuille de réponses au moment de leur visite dans le centre d’apprentissage.
Activité supplémentaire 2
Les lettres secrètes
Remettre à chaque élève une grille de nombres (annexe 1Rep.4) et des jetons.
Donner aux élèves un indice décrivant un nombre précis; par exemple, 2 dizaines et 5 unités.
Leur demander de recouvrir ce nombre avec un jeton dans leur grille de nombres.
Continuer jusqu’à ce que les jetons forment un motif représentant les deux lettres secrètes H et I
(2, 12, 22, 32, 42, 52; 5, 15, 25, 35, 45, 55; 33, 34; 8, 18, 28, 38, 48, 58).
Exemples d’indices :
(Adapter les indices au degré de compréhension du groupe d’élèves.)
- 2 dizaines et 5 unités
- entre 27 et 29
- le double de 11
- après 17
- le double de 4
- 5 dizaines et 8 unités
- 3 à la position des dizaines et 3 à la position des unités
- après 34
- 10 moins 5
- après 47
- 10 plus 2
- entre 41 et 43
- après 1
- 5 de moins que 20
- 5 de plus que 40
- 10 de plus que 22
- 10 de moins que 48
- avant 53
- 3 dizaines et 4 unités
- 50 plus 5
Enrichir l’activité en demandant aux élèves de créer leurs propres lettres secrètes, comme leurs initiales, ou un dessin simple.
Leur dire d’ombrer les lettres sur une grille de nombres, puis de rédiger des indices appropriés au verso.
Leur préciser de faire une mise à l’essai avec une ou un partenaire afin de s’assurer que les indices sont appropriés.
Mettre les feuilles d’indices dans un centre d’apprentissage avec d’autres grilles de nombres et des jetons pour que les élèves puissent les résoudre pendant les activités libres.
Activité supplémentaire 3
Les grilles de nombres
Utiliser, en début d’année, des cartes de nombre de 1 à 30 et ajouter des nombres au fur et à mesure que les élèves progressent.
Activités à partir de grilles de nombres
Nombres mêlés
Mêler les cartes de nombres dans les pochettes de la grille de nombres avant que les élèves arrivent dans la salle de classe.
Dire aux élèves : « Il y a des nombres qui ne sont pas à leur place. Qui peut m’aider à les remettre en ordre? » S’inspirer de l’exemple suivant.
| 1 | 3 | 2 | 5 | 6 | 7 | 8 | 4 | 9 | 10 |
| 11 | 12 | 23 | 14 | 16 | 18 | 15 | 17 | 19 | 20 |
Compléter la rangée
Ne pas écrire certains nombres dans les rangées de la grille de nombres et demander aux élèves de trouver les nombres manquants. S’inspirer de l’exemple suivant.
| 1 | 2 | 3 | |||||||
| 11 | 12 | 14 | 15 | 16 | |||||
| 21 | 22 | 23 | 24 |
Trouver le nombre
Placer les cartes de 1 à 50, face numérotée cachée, dans une grille de nombres à pochettes.
Poser aux élèves les questions suivantes : « Où est le 10? Où est le 30? Où est le 25? »
Avant et après
Revoir l’emploi des mots avant, après et entre.
Laisser des colonnes vides et demander aux élèves de trouver les nombres qui viennent avant, après et entre les nombres visibles.
| 1 | 3 | 5 | |||||||
| 11 | 13 | 15 | |||||||
| 21 | 23 | 25 | |||||||
| 31 | 33 | 35 |
Jeu du nombre secret ou des 20 questions
Remplir la grille avec les nombres de 1 à 50.
Choisir un nombre secret.
Inviter les élèves à poser des questions auxquelles on ne peut répondre que par oui ou par non pour éliminer les nombres; par exemple, une ou un élève peut poser la question « Y a-t-il un 4 à la position des unités? ». Si la réponse est non, on retire du tableau tous les nombres qui ont un 4 à la position des unités.
Encourager les élèves à poser des questions qui font en sorte que l’on peut retirer un grand nombre de cartes d’un même coup; par exemple : « Est-ce un nombre supérieur à 25? Est-ce un nombre inférieur à 25? »
Souligner que la régularité dans les rangées et les colonnes aide à reconnaître les nombres à retirer.
Régularité
Faire découvrir des régularités, par exemple, en retournant les cartes à tous les cinq nombres.
Compter à rebours
Utiliser la grille de nombres pour faire compter les élèves à rebours à partir de différents nombres.
Retirer les nombres un par un pendant que les élèves comptent à voix haute.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 117-128.
