GEEM - Learning Situation

B1. Number Sense

Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life.

Learning Situation 1: Bandages (Counting)

Duration: 2 hrs 10 min

Overall Expectations

Specific Expectations

Number
B1. Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life

B1.1 Read and represent whole numbers up to and including 50, and describe various ways they are used in everyday life

B1.3 Compare and order whole numbers up to and including 50, in various contexts

B1.4 Estimate the number of objects in collections of up to 50, and verify their estimates by counting

B1.5 Count to 50 by 1s, 2s, 5s, and 10s, using a variety of tools and strategies

Learning Goals

The purpose of this learning situation is to allow students to:

use numbers in meaningful contexts to describe situations;
count by 2s, 5s and 10s;
count from any number;
compare, by one-to-one correspondence, the objects of two sets;
classify and order elements to solve a problem;
estimate a number of objects and verify accuracy by counting.

Learning Context	Prerequisites
In the early grades, counting is both a skill and a strategy that allows the student to solve problems. The Grade 1student continues to learn the names of numbers by counting to 50. Students also begin to skip count by 2s, 5s, and 10s. This allows the student to recognize patterns and provides a valuable strategy for counting large numbers of objects. The ability to count up or down from any number becomes an important strategy for solving certain problems. However, it is important to recognize that most students find it more difficult to count down than up. In addition, some students hesitate or have difficulty rounding up, such as from 29 to 30, or have difficulty naming some numbers between 11 and 16.	In this learning situation, the student should be able to: count in ascending order up to 35; recognize numbers up to 35; read and write number symbols up to 35; match objects with one-to-one correspondence.

Learning Context

Prerequisites

In the early grades, counting is both a skill and a strategy that allows the student to solve problems. The Grade 1student continues to learn the names of numbers by counting to 50. Students also begin to skip count by 2s, 5s, and 10s. This allows the student to recognize patterns and provides a valuable strategy for counting large numbers of objects. The ability to count up or down from any number becomes an important strategy for solving certain problems. However, it is important to recognize that most students find it more difficult to count down than up. In addition, some students hesitate or have difficulty rounding up, such as from 29 to 30, or have difficulty naming some numbers between 11 and 16.

In this learning situation, the student should be able to:

count in ascending order up to 35;
recognize numbers up to 35;
read and write number symbols up to 35;
match objects with one-to-one correspondence.

Materials

Main Activity

Appendix 1D.1 (Bandages) (one copy per student)
Appendix 1D.2 (Character Silhouette) (one copy per student)
Appendix 1D.3 (Problem Solving: Bandages) (one copy per student)
Appendix 1D.4 (How many are there?) (one copy per student)
large sheet of paper
wrapping paper
markers (one red and one green)
adhesive bandages or small strips of masking tape (at least 35 per team)
box containing 35 adhesive bandages (1)
objects (for example, tokens, interlocking cubes)

Additional Materials for Activity 1

wooden sticks (10 per team)

Mathematical Vocabulary

Number names from 1 to 60

Before Learning (Warm-Up)

Duration: approximately 40 minutes

Prior to the lesson, use Appendix 1D.2 (Character Silhouette) or draw a large silhouette of the character on wrapping paper. Cut it out and hang it where students can see it. Place the box containing 35 bandages next to the silhouette.

Write the poem Band-Aids by Shel Silverstein (Appendix 1D.1) on a large piece of paper in advance and post or project it on the interactive white board.

Read the poem with the students.

Invite students to look for the numbers in the poem and circle them with a red marker.

Then ask other students to find the names of the body parts and circle them with a green marker.

Present the box of bandages and ask the students how many bandages it contains.

Active Learning (Exploration)

Duration: approximately 50 minutes

Read the poem aloud. Invite a student to point to the body parts on the large silhouette and ask the others to point to their bodies. This exercise will help them realize that there are many bandages on the character.

Form teams of two.

Provide each group with a copy of Appendices 1D.2 and 1D.3 and provide them with manipulatives such as tokens, a tally board, bandages, masking tape.

Introduce the problem: "Are there more bandages on the character or in the box? How do you know?

Encourage students to discuss with a partner their strategy for solving the problem. This discussion allows them to realize that there is more than one way to find the solution. Partners who have proposed different strategies must then decide which one to choose.

Circulate as students work and ask questions to stimulate thinking such as:

How will you count the bandages on the character?
How are you going to determine which has the most bandages?
How are you going to determine which has the least bandages?
What strategy did you use to solve the problem?

Display the students' solutions.

Consolidation of Learning

Duration: approximately 40 minutes

Ask each team to share their strategy for solving the problem with the class.

Count the bandages, with students, by placing them on the large silhouette.

Ask students the following questions:

How does your count compare?
How did you determine the number of bandages on the character?
How did you determine if there were more bandages on the character or in the box?

Highlight:

that there are several ways to count bandages (for example, counting by 1 or in increments of 2, 5, and 10).
that grouping makes it easier to count a large number of objects.
that the one-to-one correspondence makes it possible to solve the problem without counting.

Examples of Success Criteria

The student:

explains the problem in their own words;
looks for new strategies;
selects appropriate manipulatives;
groups objects together to facilitate counting;
clearly explains the strategy used.

Differentiated Instruction

The activity can be modified to meet different student needs.

To Facilitate the Task

Provide students with their own copy of the silhouette with bandages taped to it. Suggest various strategies that can be used to count the bandages accurately (for example, make an X on each bandage as you count, peel off the bandages, and make groups of 1, 2, or 5 before counting them).

Follow-Up at Home

How many are there?

At home, students can count various objects such as doors, windows, spoons, forks, lamps, clocks.

Give each student a copy of Appendix 1D.4 (How Many?) to be completed with a family member.

Additional Activity 1

Bead Strings

Assign a different number to each student based on their understanding of number. Have them make a counting necklace (bead necklace, cereal necklace, or interlocking cubes) to represent the number.

Increase the difficulty by having them make necklaces showing skip counting by 2s, 5s, or 10s; for example, students can alternate colours or materials, or insert paper shapes or other objects between each group of 2s, 5s, or 10s.

Ask them to exchange necklaces and count the elements.

Keep the necklaces; they can be used as concrete materials for students or to help students count.

Additional Activity 2

Let's Go For A Walk

Ask students to estimate the number of steps it would take to walk across the classroom from one end to the other.

Ask them to walk the distance while counting the number of steps required to verify their answer.

Form teams of two and ask them to come up with a strategy to determine the number of steps it takes to get from the classroom to the school office or gym.

Have each team test their strategy to find the answer.

If teams cannot come up with a strategy suggest they use sticks to represent 10 steps. One student counts and walks while the other holds the sticks. Each time the counting student gets to 10, they pause and their partner gives them a stick. At the end, students can count each group of 10 (represented by a stick) to determine the total number of steps.

Invite each team to say the number of steps between the two locations and explain the strategy they used to count the steps without making mistakes.

Record each team's answers on the board for comparison and discuss why each team did not get exactly the same number of steps.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 85-90.

Learning Situation 2: The Big Catch (Quantity)

Duration: 2 hours

Overall Expectations

Specific Expectations

Number
B1. Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life

B1.1 Read and represent whole numbers up to and including 50, and describe various ways they are used in everyday life

B1.2 Compose and decompose whole numbers up to and including 50, using a variety of tools and strategies, in various contexts.

B1.4 Estimate the number of objects in collections of up to 50, and verify their estimates by counting

B1.5 Count to 50 by 1s, 2s, 5s, and 10s, using a variety of tools and strategies.

Learning Goals

This learning situation helps the student:

estimate quantities of objects from a benchmark;
recognize various visual representations of numbers from dot plates.

Learning Context	Prerequisites
The student must develop a sense of quantity or number of objects contained in various sets. Quantity estimation should be acquired as early as possible. In the early grades, the student is most successful in estimating quantities when given a fixed choice, for example, "Are there approximately 5 or 10 objects?", "Are there approximately 20 or 30?" Questions like these lead the student, who has not developed a good number sense, to make more accurate estimates. The student also learns to use a benchmark to improve their skills. For example, by first visualizing the space occupied by 20 marbles in a jar, they can more easily estimate a larger or smaller quantity of marbles in that jar.	In this learning situation, the student should be able to: estimate small quantities of objects; recognize various representations of numbers from 1 to 10.

Learning Context

Prerequisites

The student must develop a sense of quantity or number of objects contained in various sets. Quantity estimation should be acquired as early as possible. In the early grades, the student is most successful in estimating quantities when given a fixed choice, for example, "Are there approximately 5 or 10 objects?", "Are there approximately 20 or 30?" Questions like these lead the student, who has not developed a good number sense, to make more accurate estimates. The student also learns to use a benchmark to improve their skills. For example, by first visualizing the space occupied by 20 marbles in a jar, they can more easily estimate a larger or smaller quantity of marbles in that jar.

In this learning situation, the student should be able to:

estimate small quantities of objects;
recognize various representations of numbers from 1 to 10.

Materials

Main Activity

Appendix 1Q.1 (Target Numbers) (one copy per student)
Appendix 1Q.2 (My Home) (one copy per student)
containers (one per team of four)
small objects (centicubes, cubes, two-coloured tokens, dried beans, or buttons)
large sheets of paper;

Mathematical Vocabulary

more, less, as much

Before Learning (Warm-Up)

Duration: approximately 40 minutes

Show students a container filled with small identical objects (cubes, centicubes, counters, dried beans, or buttons).

Tell students that you are going to try to pick up 22 objects in your hand and write 22 on a large piece of paper.

Take a handful of objects and count them aloud with the students. Record the actual number of objects picked up on the sheet of paper. This will be a benchmark to use in getting closer to the target number on the next pick.

Ask students the following questions:

How many of the (object) was I trying to take?
Did I take more or less?
Did I reach my target number?
Did I take too many or too few?

Repeat the activity, trying to get closer to the target number.

Ask students again if the number of objects removed from the container is too many or too few.

Form teams of four and place a container filled with identical small objects on each table.

Have each student try to take a handful of 18 objects from the container.

Have students count the objects to verify the number of students who:

have reached the target number;
who are two objects away from the target number;
who are five objects away from the target number.

Repeat the activity, but give a different number of objects to take from the container.

Active Learning (Exploration)

Duration: approximately 50 minutes

Provide a copy of Appendix 1Q.1 to each student.

Ask students to:

choose a target number between 10 and 25 and write it in the circle on the card;
try to take the number of objects written on the card from the container without counting;
count the number of objects removed from the container individually to provide a benchmark for the next trial;
record the result of this first test in the appropriate place on the form;
then indicate whether this number is higher or lower than the target number;
repeat, trying to get closer to the chosen number.

Continue the activity until students have tried four different target numbers.

Circulate around the classroom while students are working. Observe how they work and ask questions such as:

How did you know if you took too many or too few?
Were you closer to the target number on your second try?
Why were you closer to the target number the second time?
After playing several times, was it easier to get close to the exact number of objects?

Consolidation of Learning

Duration: approximately 30 minutes

Gather the students and ask them the following questions:

What was your highest target number?
What was your lowest target number?
How did you know if you took too many or too few?
Were you closer to the target number on the second try?
Why were you closer to the target number the second time?
After playing several times, was it easier on the first try to get close to the exact number of objects? Why or why not?

Point out to students that the number of objects removed on the first try served as a benchmark to help them get as close as possible to the target number on the second try.

Examples of Success Criteria

The student:

improves the accuracy of their grab on the second try;
makes increasingly accurate estimates;
determines if they have taken more, fewer, or as many objects as the target number;
correctly uses the words: plus, minus, and equal.

Differentiated Instruction

The activity can be modified to meet the needs of the students.

Follow-Up at Home

My Home

At home, the student can point to objects that are in small quantities, large quantities, or fixed quantities.

Give a copy of Appendix 1Q.2 to each student to complete the activity.

Learning Situation 3: The Exchange Game (Representation)

Duration: 2 hrs 30 min

Overall Expectations

Specific Expectations

Number
B1. Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life

B1.1 Read and represent whole numbers up to and including 50, and describe various ways they are used in everyday life

B1.2 Compose and decompose whole numbers up to and including 50, using a variety of tools and strategies, in various contexts.

B1.3 Compare and order whole numbers up to and including 50, in various contexts.

B1.4 Estimate the number of objects in collections of up to 50, and verify their estimates by counting

B1.5 Count to 50 by 1s, 2s, 5s, and 10s, using a variety of tools and strategies.

Learning Goals

The purpose of this context is to help the student:

illustrate different ways of representing numbers using concrete materials;
determine the number of tens and ones in a set;
determine the value of a digit according to its position in a number;
use the words tens and ones to describe the representation of numbers.

Learning Context	Prerequisites
In Grade 1, students continue to discover the many ways numbers can be represented. They know that numbers represent quantities and that they can be represented by objects. The various representations provide information about what numbers are, and their decompositions. In Grade 1, students are introduced to the concept of place value and its role in the representation of numbers. Although the Grade 1 student is able to count to 50 and is becoming more successful at representing numbers with concrete materials, sets still appear to them as groups of individual elements; for example, a Grade 1 student who is asked to represent the number 23 with objects may show three tokens to represent the three ones and only two tokens to represent the other 20. They often have difficulty grasping the idea that a group of 10 elements can be represented by the number 1 in a number like 11.	In this learning situation, the student should be able to: count to 50; read numbers to 50; count by 2s, 5s and 10s. The student must also have been introduced to the concept of conservation of number.

Learning Context

Prerequisites

In Grade 1, students continue to discover the many ways numbers can be represented. They know that numbers represent quantities and that they can be represented by objects. The various representations provide information about what numbers are, and their decompositions. In Grade 1, students are introduced to the concept of place value and its role in the representation of numbers. Although the Grade 1 student is able to count to 50 and is becoming more successful at representing numbers with concrete materials, sets still appear to them as groups of individual elements; for example, a Grade 1 student who is asked to represent the number 23 with objects may show three tokens to represent the three ones and only two tokens to represent the other 20. They often have difficulty grasping the idea that a group of 10 elements can be represented by the number 1 in a number like 11.

In this learning situation, the student should be able to:

count to 50;
read numbers to 50;
count by 2s, 5s and 10s.

The student must also have been introduced to the concept of conservation of number.

Materials

Main Activity

Appendix 1Rep.1 (Place Value Mat) (one copy per student)
large sheets of paper
a marker
containers with 35 counters (one per student)
sheets of paper
place value kit:
- wooden sticks, interlocking cubes, or centicubes (60 per student)*;
- pipe cleaners (4 per student);
- reusable plastic bags (one per student)
dice (one die per team)
toothpicks (36)

* wooden sticks, interlocking cubes, or centicubes are preferred to the base 10 material that is more appropriate for an older age group to represent place value.

Additional Activity 1

Appendix 1 Rep.2 (It's In the Bag!) (one copy per pair)
Appendix 1Rep.3 (Contents of the Bags)
a marker
reusable plastic bags (30)
small objects

Additional Activity 2

Appendix 1Rep.4 (1 to 60 Chart) (one copy per student)
counters

Additional Activity 3

number grid with transparent pockets
number cards from 1 to 50 for the numbers grid

Mathematical Vocabulary

tens, ones, exchange, group, place value

Before Learning (Warm-Up)

Duration: approximately 40 minutes

Before students enter:

draw 35 smiley faces on a large sheet of paper, arranging them in such a way that there are no visible rows or columns, and laminate it. Alternatively project 35 smiley faces, arranged so that there are no visible rows or columns;

place a container of 35 counters, a piece of paper, and a pencil on each student's desk.

Direct students' attention to the large sheet of paper/projection and ask them to estimate the number of faces. They may try to count them by pointing to them, but it will be difficult.

Write all estimates on the board.

Ask students to think of different ways to count them; for example, counting in groups of 2, 5 and 10.

Tell students that in the container on their desk, there are the same number of counters as there are faces on the large sheet.

Suggest that students use the tokens to represent different ways of counting the faces, for example, in groups.

After a few minutes, ask them, "What ways did you find to count the counters?" Ask the student who suggests a grouping of 2, 5, or 10 to explain it.

Gather students around the large sheet of paper and ask them to name the best way to count the faces from among those presented and explain their answer.

Circle groups of 10 smiley faces.

Have students count the groups of 10 and the remaining faces.

Write on the board:

\(\ 3 \ \mathord{groups\ of\ 10\ smileys}\)
\(= 10 + 10 + 10\)
\(= 30\)

\(\ + 5 \ \mathord{ smileys}\)
\(\ + 1 + 1 + 1 + 1 + 1\)
\(\ + 5\)

Ask students the following question: How many smiley faces are there in total? Write "= 35".

Point out to the students that 3 groups of 10 and 5 ones correspond to the number 35.

Point out that groups of 10 are called tens and single faces are called ones.

Ask students the following question: How can we remember the words tens and ones?

Active Learning (Exploration)

Duration: approximately 60 minutes

Part 1

Explain to students that today, everyone is going to make a place value kit. To do this, give each student 50 sticks, 3 pipe cleaners, and a plastic bag.

Have students make 3 bundles of 10 sticks and tie each bundle with a pipe cleaner, then keep the 20 sticks that remain untied.

Ask students the following questions:

How many packages of 10 sticks do you have?
How many unattached sticks do you have?
What name is given to the bundles of sticks that are grouped together?
Why are the packages called tens?
What is the name given to unattached sticks?
Why are they called ones?
How many sticks are there in total?

Write on the board:

\(\ 3 \ \mathord{tens}\)
\(= 10 + 10 + 10\)
\(= \ \ \ \ \ \ \ 30\)
\(= \ \ \ \ \ \ \ 50\)

\(\ + 20 \ \mathord{ones}\)
\(\ + \ \ \ \ 20\)
\(\ + \ \ \ \ 20\)

Provide each student with a copy of Appendix 1Rep.1 and explain that the place value mat is used to represent numbers by tens and ones.

Project a place value mat and show how to represent the number 16 using sticks: a pack of 10 sticks in the tens column and 6 sticks in the ones column.

Ask students to use their kit to represent the number 25 on their mat.

Invite a student to say what the student did and illustrate it on the screen with sticks.

Ask students to come up with a second way to represent 25, then a third, and illustrate their suggestions on the screen.

Point out that 25 ones or 2 packages of 10 and 5 ones or a package of 10 and 15 ones are various representations of 25.

Continue the activity by asking students to represent the following numbers: 12, 7, 18, 20 and 36.

Have students illustrate each number with sticks and ask the questions below for each:

How many tens did you use to illustrate this number?
How many units did you use to illustrate this number?
Are there other ways to represent this number?

Note: It is important to vary the manipulatives in the kit, offering tools such as interlocking cubes or 10 frames.

Part 2

Teach students to play the Swap Game, which can be played in pairs, threes or fours.

Ensure that each student has a place value kit and a copy of the place value mat (Appendix 1Rep.1).

Explain to students that one of the rules of the trading game is that you can never have more than 9 sticks in the ones column. When there are more than 9 ones in the column, trade 10 ones for a 10-pack and put all 10-packs in the tens column.

Ask students to explain the reason for placing the packages of 10 in the tens column.

Model the game and tell students to put the same number of sticks on their own place value mat.

Roll the die. If the 6 comes up, put 6 sticks in the ones column.
Roll the die again. If 2 comes up, add 2 sticks to the ones column and ask students to say how many ones there are now (8).
Roll the die again. If the 4 comes up, add 4 sticks to the ones column and ask students to say how many ones there are now (12).

Say, "What's the rule?

Let the students realize that they need to exchange the 10 sticks for a pack of 10 and put it in the tens column.

Ask students the following questions:

What do you have on your mat? (1 ten and 2 ones)
How many sticks is that? (12)

Remember that what has changed is not the number, but only its representation.

Continue to play until the number reaches or exceeds 30 and question the students after each roll of the die.

Have students play in teams. They take turns rolling the die, adding sticks to their mat and, when the time comes, exchanging 10 ones for a ten. The student who is the first to get 3 tens (30) wins.

Play this game often throughout the year. Store mats, place value kits, and dice in a bin so that students have access to the materials during free activity time.

Variant

Modify the rules of the game to play from 30 to 0 later in the year. To do this, students put three packs of 10 in the tens column as a starting point and unpack to subtract the numbers the die indicates. This activity gradually introduces them to the concepts of decomposition and regrouping in the addition and subtraction of two-digit numbers.

Consolidation of Learning

Duration: approximately 50 minutes

Join a team of four while the others continue their game.

Ask students to represent the number 27 without their place value mat.

Allow plenty of room for discussion during the work so that each student can describe what is being done in their own words.

Ask the student a few questions when the explanations are not clear:

How did you represent the number 27?
Are there other ways to represent this number? (The student may say that 27 is 2 tens and 7 ones, one ten and 17 ones, or 27 ones.)
How many groups of 10 did you make?
How many ones did you place on the mat?
Where did you place the tens?
Where did you place the ones?
After making packs of 10 ones, how many ones are left?
Why are you making a 10 pack now?
What does the number 2 represent in the number 27?
What does the number 7 represent in the number 27?
How many tens are there in the number 27?
How many total ones are there in the number 27?
Which representation best matches the way the numbers are written? (2 packs of 10 and 7 ones)

Emphasize that 2 tens and 7 ones have the same value as 27 ones. The representation may be different, but the quantity remains the same.

Circulate among and observe students during exchanges, and record, in an anecdotal record, observations about their skills in representing numbers, grouping ones into tens, and explaining strategies.

Examples of Success Criteria

The student:

represents the numbers exactly;
represents a number in different ways;
explains that a quantity does not change, even if its representation is different;
uses the words tens and ones correctly;
uses words such as too, group, pack, and swap to explain what the student is doing.

Differentiated Instruction

The activity can be modified to meet the needs of the students.

To Facilitate the Task

Work longer on representing numbers on the place value mat before moving on to the actual game.
Start with small numbers and slowly progress to larger numbers.

Follow-Up at Home

Exchange Game

At home, students can teach and play the exchange game with family members.

Ensure that the student is familiar with the rules of the game before allowing them to take a place value kit home.

Additional Activity 1

Creation of a Place Value Centre

Number 30 plastic bags using masking tape and a marker.

Group students into teams of two and give each team a copy of Appendix 1Rep.2.

Give one to four bags to each team.

Ask students to put a different quantity of various objects in each bag; for example, bag #2: 26 marbles; bag #27: 54 chips.

Tell them:

write the number of the bag and the number of objects in each bag on their answer sheet (Appendix 1Rep.2);
indicate the different groups of tens and ones that can represent the number of objects in the bag.

Example:

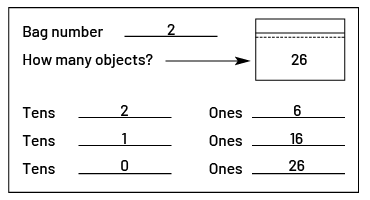
List the contents of all bags (quantity and names of elements) using Appendix 1Rep.3.

Place copies of Appendix 1Rep. 2 and the bags in a learning centre for students to use during free activity time.

Have students select different bags and complete a new answer sheet when they visit the learning centre.

Additional Activity 2

The Secret Letters

Give each student a number grid (Appendix 1Rep.4) and counters.

Give students a clue describing a specific number; for example, 2 tens and 5 ones.

Have them cover that number with a counter in their number grid.

Continue until the counters form a pattern representing the two secret letters H and I

(2, 12, 22, 32, 42, 52; 5, 15, 25, 35, 45, 55; 33, 34; 8, 18, 28, 38, 48, 58).

Examples of clues:

(Adapt the cues to the level of understanding of the group of students)

2 tens and 5 ones
between 27 and 29
double of 11
after 17
double of 4
5 tens and 8 ones
3 in the tens position and 3 in the ones position
after 34
10 minus 5
after 47
10 plus 2
between 41 and 43
after 1
5 less than 20
5 more than 40
10 more than 22
10 less than 48
before 53
3 tens and 4 ones
50 plus 5

Enrich the activity by having students create their own secret letters, such as their initials, or a simple drawing.

Tell them to shade the letters on a number grid, then write appropriate clues on the back.

Tell them to try their clues with a partner to ensure that the clues are appropriate.

Put the clue sheets in a learning centre with other number grids and counters for students to solve during free activities.

Additional Activity 3

Number Grids

Use number cards from 1 to 30 at the beginning of the year and add numbers as students progress.

Activities Using Number Grids

Mixed Numbers

Place the number cards randomly into the number grid pockets before students arrive in the classroom.

Tell students, "There are some numbers that are out of place. Who can help me put them back in order?" Use the following example as a guide.

Complete the Row

Do not write some numbers in the rows of the number grid and ask students to find the missing numbers. Use the following example as a guide.

Find the Number

Place the cards from 1 to 50, face down, in a pocket number grid.

Ask students the following questions: "Where is 10? Where is 30? Where is 25?

Before and After

Review the use of the words before, after, and between.

Leave columns empty and ask students to find the numbers that come before, after, and between the visible numbers.

Secret Number Game or 20 Questions

Fill in the grid with numbers from 1 to 50.

Choose a secret number.

Invite students to ask yes/no questions to eliminate numbers; for example, a student might ask, "Is there a 4 in the ones position?" If the answer is no, all numbers with a 4 in the ones position are removed from the chart.

Encourage students to ask questions that result in a large number of cards being removed in one move; for example, "Is this a number greater than 25? Is this a number less than 25?

Point out that the patterns in the rows and columns helps them recognize the numbers to be removed.

Pattern Rule

Have students discover patterns, for example, by turning over every fifth card.

Counting Backwards

Use the number grid to have students count backwards from different numbers.

Remove the numbers one at a time while students count aloud.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 117-128.