B1.6 Utiliser des schémas pour représenter et résoudre des problèmes de partage équitable d’un tout pouvant comprendre jusqu’à 10 éléments entre 2, 3, 4 et 6 personnes, y compris des problèmes dont le résultat est un nombre naturel, un nombre fractionnaire ou une fraction, et comparer les résultats.
Activité 1 : partage équitable entre 3 personnes
Présenter aux élèves la situation suivante.
Axel désire partager équitablement les gommes qui lui restent dans son paquet avec 2 de ses amis. Il a 7 morceaux de gomme à partager. Afin que chaque personne reçoive la même quantité, comment pourrait-il partager les morceaux de gomme?
Exemples
Stratégie 1
Modèle de surface à l’aide du géoplan
Un élève peut utiliser le géoplan pour représenter le partage des 7 morceaux de gomme entre les 3 amis. En premier, l’élève distribue 1 morceau de gomme entier à chaque enfant, puis en distribue un deuxième.

Le géoplan est pointillé à huit par douze. Au-dessus, il y a trois noms : Axel, Ami un, Ami deux. Sous Axel, il y a deux points par quatre points reliés, ce qui forme un rectangle violet dans lequel entreraient trois carrés. En dessous, il y a un rectangle violet identique, et un rectangle blanc de la même grosseur. Sous Ami un et Ami deux, il y a respectivement deux rectangles violets de la même grosseur.
On remarque qu’il reste un morceau de gomme à partager équitablement. L’élève peut donc le séparer en 3 parties égales, soit en tiers, et donner un tiers à chaque ami.
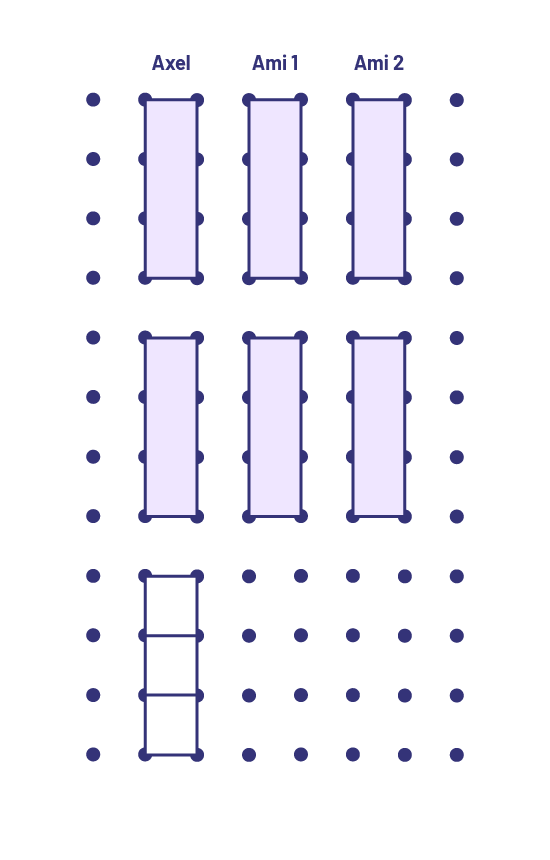
Le géoplan est pointillé à huit par douze. Au-dessus, il y a trois noms : Axel, Ami un, Ami deux. Sous Axel, il y a deux points par quatre points reliés, ce qui forme un rectangle violet dans lequel entreraient trois carrés. En dessous, il y a un rectangle violet identique, et un rectangle blanc de la même grosseur. Celui-ci est divisé en trois pour montrer les trois carrés. Sous Ami un et Ami deux, il y a respectivement deux rectangles violets de la même grosseur.

Le géoplan est pointillé à huit par douze. Au-dessus, il y a trois noms : Axel, Ami un, Ami deux. Sous Axel, sous Ami un et sous Ami deux respectivement, il y a deux points par quatre points reliés, ce qui forme un rectangle violet dans lequel entreraient trois carrés. Le même rectangle est répliqué en dessous pour les trois noms. Et sous celui-ci, pour les trois noms, l’on trouve un carré blanc.
Chaque enfant recevra alors 2 et un tiers morceaux de gomme.
Stratégie 2
Schéma à l’aide d’un modèle de surface
Une élève pourrait décider de couper les 7 gommes en 3 parties égales, puisqu’elle sait qu’ils sont 3 enfants. Elle partage par la suite les parties (1 un tiers) à chaque élève.

Sous le texte « une gomme en trois parties égales », il y a trois carrés violets placés l’un sous l’autre. Le premier carré a une flèche qui pointe à droite, vers un carré identique à côté duquel il est écrit Axel. Le deuxième carré pointe aussi à droite vers un carré identique à côté duquel il est écrit Ami un. Et le troisième carré a lui aussi une flèche qui pointe vers la droite vers un carré identique à côté duquel il est écrit Ami deux.
Par la suite, l’élève fait le même partage avec les autres morceaux de gomme, et ce, jusqu’à ce qu’il n’y ait plus de parties à partager.
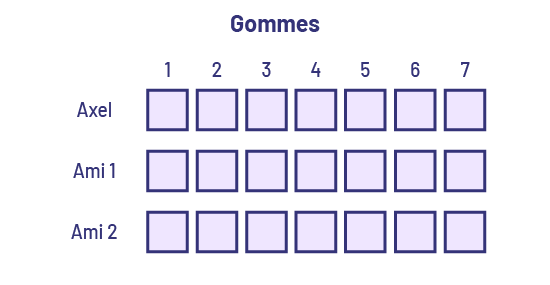
Chaque enfant reçoit 7 un tiers de morceaux de gomme.
Poser aux élèves des questions telles que :
- Quelles stratégies peut-on utiliser pour partager de façon équitable les morceaux de gomme?
- Existe-t-il plus d’une réponse possible? Pourquoi?
- À l’aide de mots, comment peut-on décrire les parts résultant du partage?
Activité 2 : partage équitable entre 6 personnes
Présenter aux élèves la situation suivante.
Isabella prépare 6 bols de salade pour elle et ses 5 convives. Il lui reste 5 morceaux de céleri seulement. Comment peut-elle partager de façon équitable les 5 morceaux de céleri dans les 6 bols?
Exemple
L’élève partage 5 morceaux de céleri entre 6 personnes.

Au-dessus de la file de céleris, le nom Isabella part du début du premier céleri et s’arrête entre le cinquième et le sixième morceau de ce céleri. Ensuite, le nom « premier ou première convive » part de cet endroit et s’arrête entre le quatrième et le cinquième morceau du deuxième céleri. Ensuite, le nom « deuxième convive » part de cet endroit et s’arrête entre le troisième et le quatrième morceau du troisième céleri. Ensuite, le nom « troisième convive » part de cet endroit et s’arrête entre le deuxième et le troisième morceau du quatrième céleri. Ensuite, le nom « quatrième convive » part de cet endroit et s’arrête entre le premier et le deuxième morceau du cinquième céleri. Enfin, le nom « cinquième convive » part de cet endroit et s’arrête au sixième morceau du cinquième céleri.
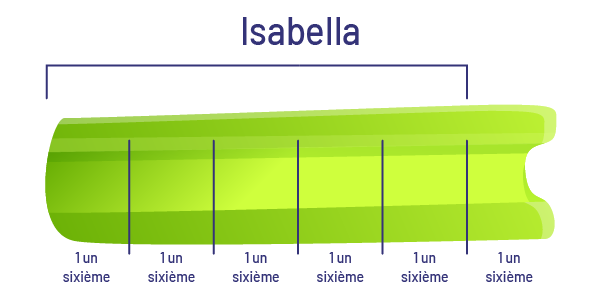
Chaque personne reçoit 5 un sixième d’un morceau de céleri.
Poser aux élèves des questions telles que :
- Quelles stratégies peut-on utiliser pour partager de façon équitable les morceaux de céleri dans les 6 bols?
- Existe-t-il plus d’une réponse possible? Pourquoi?
- À l’aide de mots, comment peut-on décrire les parts résultant du partage?
Activité 3 : idées pour explorer les fractions
Représenter les fruits d’une salade de fruits à l’aide de fractions; par exemple, \(\frac{1}{4}\) de fraises, \(\frac{1}{4}\) de melon d’eau, \(\frac{1}{4}\) d’ananas et \(\frac{1}{4}\) de pêches.
Présenter aux élèves une croustade aux pommes (en forme de carré) et leur demander la partie qu’elles et ils aimeraient manger (\(\frac{1}{2}\), \(\frac{1}{3}\) ou \(\frac{1}{4}\)) et d’expliquer leur choix.
En sciences, lorsque les élèves classifient les animaux, représenter les résultats à l’aide de fractions; par exemple, \(\frac{1}{3}\) des animaux nagent, \(\frac{1}{3}\) des animaux volent, \(\frac{1}{3}\) des animaux sautent.
Présenter aux élèves le jeu suivant qui se joue en équipes de deux. À tour de rôle, un des membres de l’équipe prend une poignée d’objets. Si la quantité d’objets se divise en \(\ 2 \ ( \frac{1}{2})\), il a deux points, si elle se divise en \(\ 3 \ ( \frac{1}{3})\), il a trois points et si elle se divise en \(\ 4 \ ( \frac{1}{4})\), il a 4 points.
Demander aux élèves de préparer un ragoût en représentant les légumes à l’aide de cubes de différentes couleurs; par exemple, un ragoût avec \(\frac{1}{4}\) de carottes (cubes orange), \(\frac{2}{4}\) de pommes de terre (cubes blancs) et \(\frac{1}{4}\) de haricots verts (cubes verts).
Présenter aux élèves le problème suivant. En éducation physique, deux amis font une course. Un ami a parcouru la moitié (\(\frac{1}{2}\)) de la distance et l’autre a parcouru \(\frac{1}{4}\) de la distance. Lequel est en train de gagner?
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activité 4 : du plus petit au plus grand (comparaison de résultats)
Démarche
Remettre aux élèves une liste aléatoire de fractions simples (par exemple, \(\frac{1}{2}\), \(\frac{1}{4}\) et \(\frac{1}{3}\)).
Demander aux élèves de les placer en ordre croissant en utilisant du matériel de manipulation.
Demander aux élèves d’expliquer leur séquence et de la justifier.
Note : Représenter ces fractions avec du matériel concret en respectant les quatre modèles : modèle de longueur (par exemple, droite numérique), modèle de surface (par exemple, cercle fractionnaire), modèle de volume (par exemple, verres remplis d’eau) et modèle d’ensemble (par exemple, jetons). Il est important que les élèves sachent ce que représente chaque fraction en fonction des modèles et soient en mesure de déterminer la fraction qui est la plus grande.
Intervention
Circuler dans la salle de classe et poser aux élèves des questions telles que :
- Quelle fraction est la plus grande? la plus petite? Comment le sais-tu?
- Que représente chaque nombre dans une fraction?
- Qu’est-ce qui est différent entre les objets que tu as utilisés pour illustrer les fractions et ceux qu’ont utilisés les autres? Qu’est-ce qui est pareil?
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 68 et 69.
