At a Glance...

Activity 1: Fair-Sharing Among 3 People

---

Present the following situation to the students.

Axel wants to share the remaining gum in his pack equally with two of his friends. He has 7 pieces of gum to share. In order for each person to receive the same amount, how could he share the pieces of gum?

Examples

Strategy 1

Area model using the geoboard

A student can use a geoboard to represent the division of the 7 pieces of gum among the 3 friends. First, the student distributes 1 whole piece of gum to each child, then distributes a second piece.

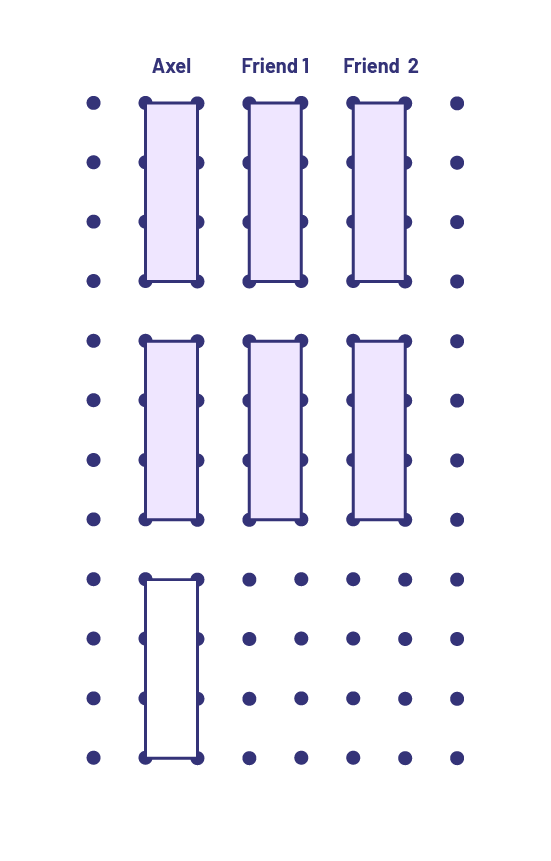
Notice that there is one piece of gum left to share equally. The student can then separate it into 3 equal parts, or thirds, and give one third to each friend.

Each child will then receive 2 and one third pieces of gum.

Strategy 2

Area Model on a Diagram

A student might decide to cut the 7 each of the pieces of gum into 3 equal parts, since tthere are 3 children. They then distribute the parts (1 one third) to each student.

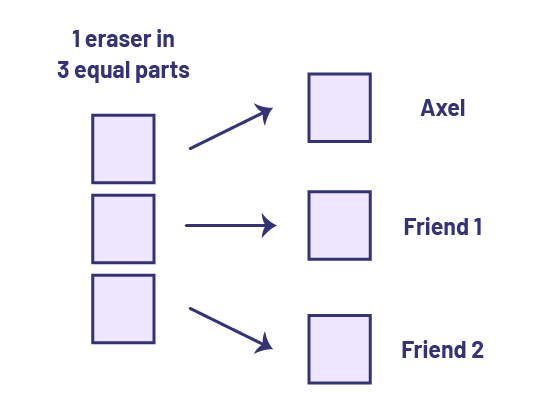
Then the student does the same sharing with the other pieces of gum until there are no more parts to share.

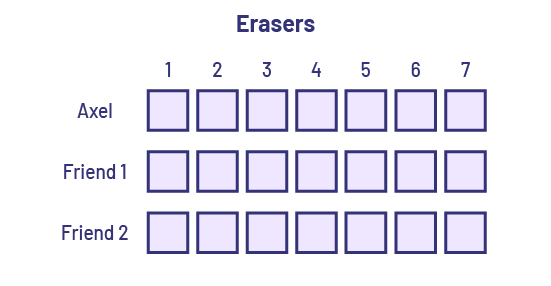
Each child is given one thirds of a piece of gum.

Ask questions such as:

• What strategies can be used to share the gum pieces equally?
• Is there more than one possible answer? Why or why not?
• Using words, how can you describe the parts resulting from sharing?

Activity 2: Fair-Sharing Among 6 People

---

Present the following situation to students.

Isabella prepares 6 bowls of salad for herself and her 5 guests. She has only 5 pieces of celery left. How can she divide the 5 pieces of celery equally among the 6 bowls?

Example

The student shares 5 pieces of celery among 6 people.

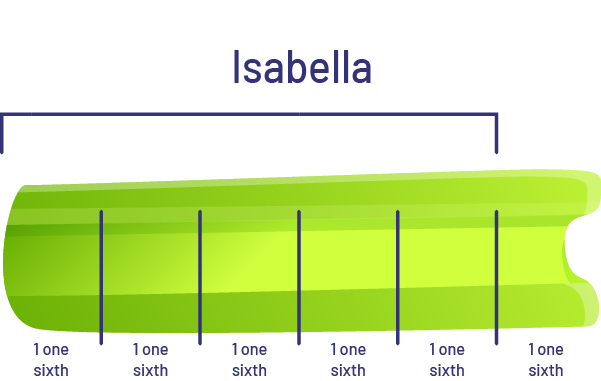
Each person receives 5 one sixths of a piece of celery.

Ask questions such as:

• What strategies can be used to share the celery pieces equally among the 6 bowls?
• Is there more than one possible answer? Why or why not?
• Using words, how can you describe the parts resulting from sharing?

Activity 3: Ideas for Exploring Fractions

---

Represent the fruit in a fruit salad using fractions; for example, strawberries, watermelon, pineapple, and peaches.

Present students with an apple crisp (in the shape of a square) and ask them which part they would like to eat \(\frac{1}{2}\), \(\frac{1}{3}\) or \(\frac{1}{4}\) and explain their choice.

In science, when students classify animals, represent results using fractions; for example, \(\frac{1}{3}\) animals swim, \(\frac{1}{3}\) animals fly, \(\frac{1}{3}\) animals jump.

Introduce the students to the following game which is played in teams of two. In turn, one of the team members takes a handful of objects. If the quantity of objects divides into \(\ 2 \ ( \frac{1}{2})\), they get two points, if it divides into \(\ 3 \ ( \frac{1}{3 })\), they get three points and if it divides into \(\ 4 \ ( \frac{1}{4})\), they get 4 points.

Have students prepare a stew by representing the vegetables with different coloured cubes; for example, a stew with carrots (orange cubes), potatoes (white cubes), and green beans (green cubes).

Present students with the following problem. In physical education, two friends are running a race. One friend has covered half (\(\frac{1}{2}\)) of the distance and the other has covered \(\frac{1}{4}\) of the distance. Who is winning?

Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).

Activity 4: From Smallest to Largest (Comparison of Results)

---

Directions

Hand out a random list of unit fractions (for example, \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{3}\)).

Have students place them in ascending order using manipulatives.

Ask students to explain their sequence and justify it.

Note: Students should have experience representing these fractions with concrete materials using four models: linear model (for example, number line), area model (for example, fractional circle), volume model (for example, glasses filled with water), and set model (for example, counters). It is important that students know what each fraction represents based on the models and are able to determine which fraction is greater.

Teacher Moves

Circulate around the classroom and ask students questions such as:

• Which fraction is greater? Smaller? How do you know?
• What is different between the objects you used to illustrate fractions and those used by others? What is the same?

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 68 et 69.