B2.3 Utiliser des stratégies de calcul mental, y compris l’estimation, pour additionner des nombres naturels dont la somme est égale ou inférieure à 50 et pour soustraire des nombres égaux ou inférieurs à 50, et expliquer les stratégies utilisées.
Activité 1 : jeu de la « calculatrice humaine »
Inviter une ou un élève à jouer le rôle de la « calculatrice humaine ». Les élèves qui jouent ce rôle se tiennent debout, en avant de la classe, en face d’une grille de nombres reproduite sur une feuille grand format (on peut aussi utiliser une grille projetée à l’aide du tableau blanc interactif). Les autres élèves utilisent une calculatrice ordinaire.
Demander aux élèves d’entrer un nombre, par exemple 35, dans la calculatrice.
Demander à la « calculatrice humaine » de montrer du doigt 35 sur la grille de nombres. L’objectif est de voir qui va aller le plus vite, la « calculatrice humaine » ou les élèves qui utilisent une calculatrice.
Demander à la « calculatrice humaine » et aux autres élèves d’additionner 15 au nombre initial et de donner la réponse dès qu’elle est affichée à l’écran de la calculatrice. La « calculatrice humaine » déplace son doigt verticalement d’une rangée vers le bas, de 35 à 45, et horizontalement de cinq colonnes vers la droite jusqu’à 50.
Le plus souvent, c’est la « calculatrice humaine » qui l’emporte. Les élèves peuvent jouer tour à tour le rôle de la calculatrice humaine.
Cette activité peut se faire d’abord avec le groupe-classe et, plus tard, en petits groupes.
Poser aux élèves des questions de plus en plus difficiles, comme \(35 + 10\), \(+11\), \(+12\), \(-20\), \(-30\), et ainsi de suite.
Confectionner des cartes. Écrire le nombre de départ sur un côté de la carte et le nombre à ajouter de l’autre côté. La « calculatrice humaine » met son doigt sur le nombre de départ et les autres élèves entrent ce nombre dans leur calculatrice.
Tourner la carte pour montrer aux élèves le nombre à ajouter. Ne pas écrire toute la question sur le même côté de la carte, car les élèves qui utilisent une calculatrice risquent d’être plus rapides.
Cette activité habitue les élèves à additionner par dizaines et non par unités.
Activité 2 : le nombre mystère
Matériel
- annexe 2D.1 (une copie par élève)
- jetons (un par élève ou par équipe)
Remettre une copie de l’annexe 2D.1 et un jeton à chaque élève ou à chaque équipe de deux.
Demander aux élèves de placer leur jeton sur un nombre de départ, comme 54.
Dessiner une flèche ou une série de flèches sur une grille vierge.
Inviter les élèves à déplacer leur jeton, une case à la fois, selon l’ordre des flèches pour déterminer le nombre mystère choisi par le personnel enseignant.
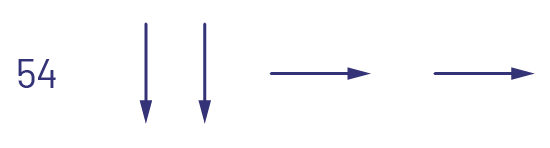
Note : La première flèche indique qu’il faut descendre d’une case, ce qui augmente le nombre de 10, pour arriver à 64. La deuxième flèche indique qu’il faut ensuite descendre d’une autre case jusqu’à 74. La troisième flèche indique qu’il faut effectuer un déplacement d’une case vers la droite jusqu’à 75. La dernière flèche indique qu’il faut effectuer un déplacement d’une autre case vers la droite pour arriver à 76, qui est le nombre mystère dans ce cas-ci. Le premier essai peut nécessiter une démonstration sur un tapis de nombres ou une grille de nombres.
Proposer aux élèves de choisir un nombre mystère, de l’écrire sur un morceau de papier et de fournir des indices sous forme de flèches à leur partenaire pour qu’elle ou il puisse découvrir ce nombre.
Demander aux élèves d’écrire la phrase mathématique qui correspond au parcours effectué pour découvrir le nombre mystère (par exemple, \(54 + 10 + 10 + 1 + 1 = 76\)).
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 144.
Activité 3 : la droite utile
Tracer une droite au tableau en n’indiquant rien d’autre que le premier terme d’une opération.
Préciser aux élèves que l’on peut utiliser une droite numérique ouverte pour représenter visuellement ce qui se passe dans notre tête pendant un calcul mental.
Exemple simple
Proposer aux élèves l’opération \(9 + 8\).
Allouer aux élèves du temps pour réfléchir, puis recueillir leurs suggestions; par exemple, une ou un élève pourrait dire : Je sais que \(9 + 1 = 10\). J’ai ensuite ajouté 7 en comptant 11, 12, 13, 14, 15, 16, 17. La réponse est donc 17.

Exemple plus complexe
Proposer aux élèves une opération telle que \(44 - 18\).
Allouer aux élèves du temps pour réfléchir, puis recueillir leurs suggestions; par exemple, une ou un élève pourrait exprimer son idée ainsi : À partir de 44, j’ai reculé de 10 pour arriver à 34. J’ai ensuite reculé de 4 jusqu’à 30, puis encore de 4 pour obtenir 26.

Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 144 et 145.
