B2.5 Représenter et résoudre des problèmes relatifs à la multiplication en tant qu’addition répétée de groupes égaux, y compris des groupes de un demi et de un quart, à l’aide d’une variété d’outils et de schémas.
Activité 1 : jeu de cercles et de points
Règles du jeu
Ce jeu se joue à deux.
La première personne qui joue :
- lance un dé et trace, sur une feuille de papier, le nombre de cercles indiqué sur le dé;
- lance le dé une deuxième fois et dessine, dans chaque cercle, le nombre de points indiqué sur le dé;
- écrit, ensuite, une phrase mathématique qui représente la multiplication (par exemple, si l’on a 3 cercles contenant 4 points chacun, il faut écrire 3 × 4 = 12).
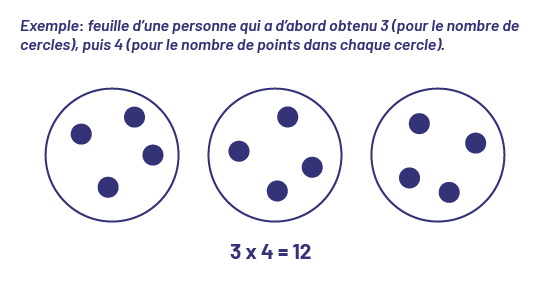
La deuxième personne répète les mêmes étapes. Elle :
- lance le dé pour connaître le nombre de cercles à tracer;
- lance le dé de nouveau pour connaître le nombre de points à dessiner dans chaque cercle;
- écrit une phrase mathématique.
Le résultat d’une multiplication s’appelle le produit. La personne qui obtient le produit le plus élevé a un point. La première personne qui obtient 10 points gagne la partie.
Activité 2 : problèmes de groupes égaux
Tout inconnu
France a acheté 5 oursons en peluche. Chaque ourson lui a coûté 2 $. Combien d’argent France a-t-elle dépensé pour l’achat des oursons en peluche?
Calculs effectués à l’aide de mes doigts
J’ai 5 doigts pour représenter les 5 oursons en peluche. Je vais compter chaque doigt par bonds de 2.
\(2 + 2 + 2 + 2 + 2 = \mathord{?}\) ou \(5 \times 2 \ \mathord{$}= \mathord{?}\)

Au-dessus du pouce, il y a le chiffre deux. Au-dessus de l’index, il y a le chiffre quatre. Au-dessus du majeur, il y a le chiffre six. Au-dessus de l’annulaire, il y a le chiffre huit. Et au-dessus de l’auriculaire, il y a le nombre dix.
Soit, 2, 4, 6, 8, 10. J’obtiens 10. France a donc dépensé 10 $ pour l’achat des oursons en peluche.
Nombre d’objets dans les groupes inconnu
France a 10 oursons en peluche. Elle veut les donner à 5 de ses amies. Combien d’oursons en peluche chaque amie recevra-t-elle si chacune en reçoit le même nombre?
Calculs effectués à l’aide de réglettes CuisenaireMC
Je prends la réglette orange qui vaut 10 unités. Je dois trouver 5 réglettes de la même valeur, qui sont égales à la réglette orange de 10. Je peux placer 5 réglettes rouges pour arriver à 10. La réglette rouge a une valeur de 2 unités. Donc, chaque amie recevra 2 oursons en peluche.
\(5 \ \times \mathord{?} = 10\) ou \(10 \div 5 = \mathord{?}\)
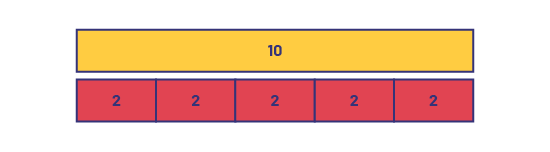
Sur la réglette orange, il y a un le nombre dix. Sur chaque réglette rouge, il y a le chiffre deux.
Nombre de groupes inconnu
France a acheté 10 oursons en peluche pour ses amies. Elle en met 2 dans chaque sac-cadeau. Combien de sacs-cadeaux France a-t-elle utilisés?
Calculs à l’aide d’une droite numérique
Il y a 10 oursons en peluche. Je sais que France en met 2 dans chaque sac-cadeau. Alors, je fais des bonds de 2 sur la droite numérique jusqu’à ce que j’arrive à 10. Je vois que j’ai fait 5 bonds de 2. Alors, France a besoin de 5 sacs-cadeaux.
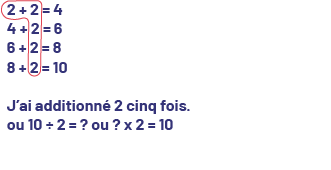
Les équations suivantes sont placées l’une sous l’autre : deux plus deux égale quatre. Quatre plus deux égale six. Six plus deux égale huit. Huit plus deux égale dix. Tous les chiffres deux sont entourés ensemble au crayon rouge pour les regrouper. En dessous, il est écrit : « J’ai additionné deux cinq fois. Ou dix divisé par deux égale point d’interrogation ou point d’interrogation multiplié par deux égale dix ».
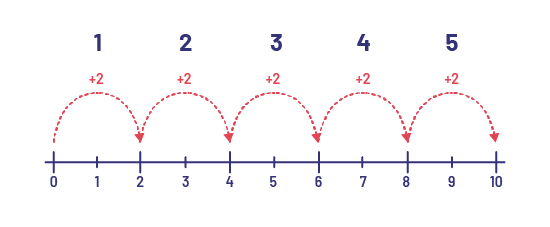
Une droite numérique est numérotée de zéro à dix. Au-dessus, des flèches courbes pointillées font des bonds de deux. Au-dessus d’elles, il est écrit « plus deux ». Et au-dessus des mentions « plus deux », il est écrit respectivement un, deux, trois, quatre et cinq.
Activité 3 : problèmes de partage égal
Exemple 1
Mélina a des réglisses rouges qu’elle aimerait distribuer à ses 6 amis. Elle décide de les couper en demis, puisqu’elles sont très longues. De combien de réglisses rouges a-t-elle besoin?
Calculs effectués à l’aide d’un schéma
Je sais que un demi plus un demi, ça fait un tout. Un autre demi plus un demi, ça fait un autre tout. Un autre demi plus un demi, ça fait un autre tout. Alors, \(1 + 1 + 1 = 3\).
\(\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \mathord{?}\) ou \( 6 \times \frac{1}{2} = \mathord{?}\)
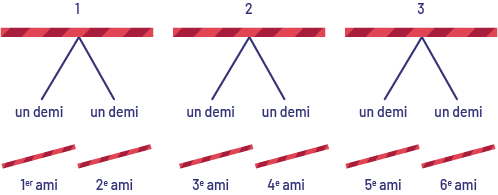
À trois reprises, un triangle sans base placé sous une réglisse pointe vers le milieu de celle-ci. Sous chaque segment, il est écrit « un demi ». Sous la première réglisse, il y a deux petites réglisses, respectivement attribuées au premier ami et au deuxième ami. Sous la deuxième réglisse, il y a deux petites réglisses, respectivement attribuées au troisième ami et au quatrième ami. Et sous la troisième réglisse, il y a deux petites réglisses, respectivement attribuées au cinquième ami et au sixième ami.
Mélina a besoin de 3 réglisses rouges.
Exemple 2
Papa veut faire de grands sous-marins pour moi et 7 membres de mon équipe de soccer. Il coupe chaque sous-marin en quarts. Chaque personne recevra un quart. Combien de sous-marins doit-il faire?
Calculs effectués à l’aide d’un schéma
\(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \mathord{?}\) ou \( 8 \times \frac{1}{4} = \mathord{?}\)
Je sais que \(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = 1 \mathord{ \ tout}\). Un sous-marin nourrit donc 4 personnes. Il y a 8 membres de l’équipe, alors il faut un autre sous-marin.
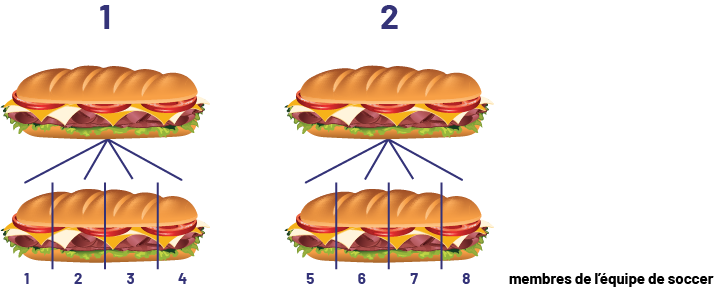
Sous le sandwich un, quatre traits pointent respectivement vers chacune des parties de son jumeau du bas, qui lui est divisé en quatre parts égales numérotées un, deux, trois, quatre. L’exercice se répète avec le sandwich deux; cependant, les parties de son jumeau du bas sont numérotées cinq, six, sept, huit. En bas à droite de l’image, il est écrit : « membres de l’équipe de soccer ».
Calculs effectués à l’aide de réglettes CuisenaireMC
Je sais qu’il y a 8 membres de l’équipe de soccer. Alors, je prends 8 réglettes blanches qui valent chacune 1 unité. Je forme des groupes de 4. J’ai deux groupes de 4. Ensuite, je trouve la réglette qui représente 4 unités, soit la réglette violette. J’ai deux réglettes violettes qui représentent les deux sous-marins.
\(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \mathord{?}\) ou \( 8 \times \frac{1}{4} = \mathord{?}\)
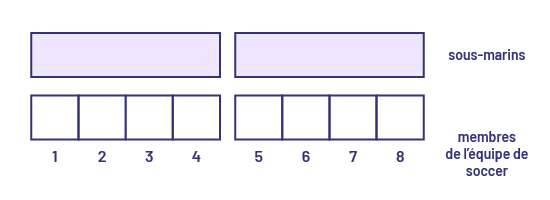
Papa doit faire 2 grands sous-marins pour les 8 membres de l’équipe de soccer.
Activité 4 : Opérations musicales (relation entre la multiplication et l’addition répétée)
Démarche
Faire jouer une pièce musicale. Dire aux élèves de circuler dans la salle de classe.
Arrêter la musique. Montrer aux élèves une carte sur laquelle est écrit un nombre divisible en parts égales (par exemple, 6, 8, 9 ou 10).
Dire aux élèves de se regrouper selon le nombre écrit sur la carte et de trouver une façon de former des sous-groupes égaux.
Demander aux élèves de déterminer et de présenter les additions et les multiplications possibles qui représentent le nombre (par exemple, pour le nombre 10, les élèves pourraient former cinq groupes et dire : \(2 + 2 + 2 + 2 + 2 = 10\) ou \(5 \times 2 = 10\). Elles et ils pourraient aussi former deux groupes et dire : \( 5 + 5 = 10\) ou \(2 \times 5 = 10\)).
Procéder de la même façon en utilisant un autre nombre.
Par la suite, montrer aux élèves des cartes sur lesquelles sont écrits de plus grands nombres divisibles en parts égales.
Intervention
Poser aux élèves des questions lorsqu’elles et ils présentent leur représentation, telles que :
- Comment est-ce que l’addition répétée ressemble à la multiplication?
- Peux-tu m’expliquer la relation entre les deux opérations?
- Quelle opération utiliserais-tu le plus entre les deux? Pourquoi?
- Peux-tu écrire, au tableau, les phrases mathématiques qui représentent la décomposition du nombre?
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 67.
