B2.5 Represent multiplication as repeated equal groups, including groups of one half and one fourth, and solve related problems, using various tools and drawings.
Activity 1: Circle and Dot Game
Rules of the Game
This game is played in pairs.
The first person to play:
- rolls a die and draws the number of circles indicated on the die on a piece of paper;
- rolls the die a second time and draws the number of dots in each circle indicated on the die;
- then writes a number sentence that represents the multiplication (for example, if there are 3 circles containing 4 points each, writes 3 × 4 = 12).
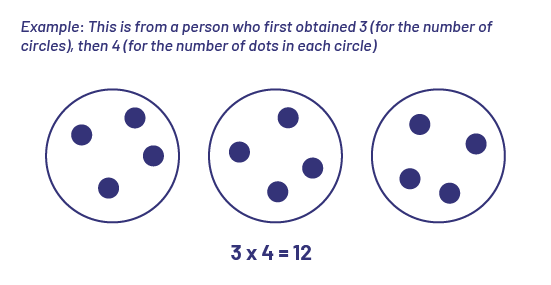
The second person repeats the same steps. They:
- roll the die to find out how many circles to draw;
- roll the die again to see how many dots to draw in each circle;
- write a number sentence.
The result of a multiplication is called the product. The person with the highest product gets one point. The first person to get 10 points wins the game.
Activity 2: Equal-Group Problems
Product Unknown
Frances bought 5 teddy bears. Each teddy bear cost her $2. How much money did Frances spend on the teddy bears?
Calculations Made With My Fingers
I have 5 fingers to represent the 5 teddy bears. I will count each finger in skips of 2.
\(2 + 2 + 2 + 2 + 2 = ?\) or \(5 \times 2 = ?\)

That is, 2, 4, 6, 8, 10. I get 10. So France spent $10 on the teddy bears.
Size of the Groups Unknown
Frances has 10 teddy bears. She wants to give them to 5 of her friends. How many teddy bears will each friend receive if they each receive the same number?
Calculations Made With Relational Rods
I took the orange rod that is worth 10 units. I had to find 5 rods of the same value, which are equal to the orange rod of 10. I found 5 red rods were the same length as the 10 rod. The red rod has a value of 2 units. So each friend will get 2 teddy bears.
\(5 \ \times \mathord{?} = 10\) or \(10 \div 5 = \mathord{?}\)

Number of Groups Unknown
Frances bought 10 teddy bears for her friends. She put 2 in each gift bag. How many gift bags did Frances use?
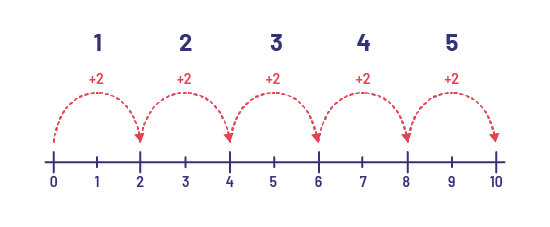
Calculations Using a Number Line
There are 10 teddy bears. I know that Frances puts 2 in each gift bag. So I skipped by 2 on the number line until I got to 10. I made 5 jumps of 2. So, I know that Frances needs 5 gift bags.
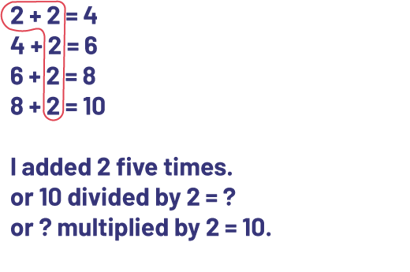
Activity 3: Equal-Sharing Problems
Below are examples of equal-sharing problems. Teachers can model these representations, but students are not expected to use fraction notation in Grade 2.
Example 1
Melina has some red licorice that she would like to distribute to her 6 friends. She decides to cut them into halves, since they are very long. How many red licorice pieces does she need?
Calculations Made With the Help of a Diagram
I know that a half plus a half is a whole. Another half plus a half is another whole. Another half plus a half is another whole. So, \(1 + 1 + 1 = 3\).
\(\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \mathord{?}\) or \( 6 \times \frac{1}{2} = \mathord{?}\)

Melina needs 3 red licorice.
Example 2
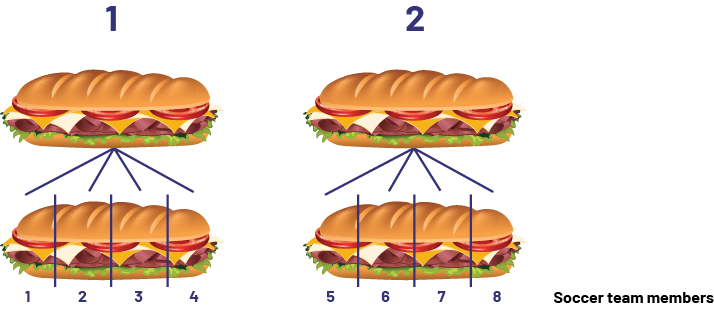
Dad wants to make big subs for me and 7 members of my soccer team. He cuts each sub into fourths. Each person will get a fourth. How many subs does he need to make?
Calculations Made With the Help of a Diagram
\(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \mathord{?}\) or \( 8 \times \frac{1}{4} = \mathord{?}\)
I know that \(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = 1 \). So one submarine sandwich feeds 4 people. There are 8 team members, so we need another submarine sandwich.
Calculations Made With Relational Rods
I know that there are 8 members of the soccer team. So I took 8 white rods, each worth 1 unit. I formed groups of 4 because dad cut each sub into fourths. I had two groups of 4. Then I found the rod that represents 4 units, the purple rod. I have two purple rods that represent the two submarine sandwiches.
\(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \mathord{?}\) or \( 8 \times \frac{1}{4} = \mathord{?}\)

Dad has to make 2 large subs for the 8 members of the soccer team.
Activity 4: Musical Operations (Relationship Between Multiplication and Repeated Addition)
Directions
Play a piece of music. Tell students to circulate around the classroom.
Stop the music. Show students a card with a number written on it that is divisible into equal parts (for example, 6, 8, 9, or 10).
Tell students to group themselves according to the number on the card.
Ask students to identify and present the possible additions and multiplications that represent the number (for example, for the number 10, students could form five groups and say: \(2 + 2 + 2 + 2 + 2 = 10\) or \(5 \times 2 = 10\). They could also form two groups and say: \(5 + 5 = 10\) or \(2 \times 5 = 10\).
Proceed in the same way using a different number.
Later, show students cards with larger numbers written on them that are equally divisible.
Teacher Moves
Ask students questions when they present their representation, such as:
- How is repeated addition like multiplication?
- What is the relationship between the two operations?
- Which operation would you be more likely to use between the two? Why?
- Write the number sentences on the board that represents the decomposition of the number into equal parts.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 67.
