B1.6 Utiliser des schémas pour représenter et résoudre des problèmes de partage équitable d’un tout pouvant comprendre jusqu’à 10 éléments entre 2, 3, 4 et 6 personnes, y compris des problèmes dont le résultat est un nombre naturel, un nombre fractionnaire ou une fraction, et comparer les résultats.
Habileté : représenter et résoudre des problèmes de partage équitable
Le développement de la compréhension de la quantité représentée par une fraction repose sur l’expérience de l’élève avec du matériel concret et sur un enseignement qui mise davantage sur le sens de la fraction que sur les procédures.
(Bezuk et Cramer, « Teaching about Fractions: What, When, and How? », dans P. Trafton (Ed.), National Council of Teachers of Mathematics 1989 Yearbook: New Directions For Elementary School Mathematics, 1989, p. 157, traduction libre)
Au cycle primaire, les élèves ont l’occasion d’explorer les fractions en partageant des ensembles d’objets (par exemple, si 3 amis veulent se partager également 18 pommes, chacun recevra \(\frac{1}{3}\) des pommes) et en examinant des touts séparés en parties équivalentes (par exemple, un rectangle séparé en quarts). Le partage peut alors servir de tremplin pour l’étude des fractions au cycle moyen. Notons qu’en 2e année, le programme-cadre circonscrit l’étude des fractions aux demis, aux tiers, aux quarts et aux sixièmes.
En continuant d’exploiter le principe de partage, les élèves créent des liens entre l’action du partage, le tout et les parties du tout. Elles et ils sont alors en mesure de mieux comprendre le fractionnement et développent un sens de la fraction. Les élèves comprennent que la fraction s’emploie aussi pour illustrer un reste à la suite d’un partage (par exemple, si 4 élèves veulent se partager 5 petits gâteaux, chacun reçoit 1 petit gâteau et \(\frac{1}{4}\) d’un petit gâteau).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
Exploration de fractions
Baroody et Coslick (Fostering Children’s Mathematical Power: An Investigative Approach to K-8 Mathematics Instruction, 1998, p. 9-14 et 9-15) privilégient une « approche signifiante » dans l’apprentissage des fractions. Ils préconisent que cet apprentissage suive une progression qui fait passer les élèves de représentations informelles et concrètes à une représentation formelle et abstraite. La première étape de cette progression est le partage de quantités.
Partager
Toute activité qui engage les élèves dans une expérience signifiante de partage, sans faire référence de manière explicite à la terminologie ou à la symbolique, leur fournit une base concrète à la compréhension du concept de fraction. En commençant par une tâche courante du quotidien (par exemple, le partage de crayons-feutres ou de crayons de couleur pour un projet d’art), les élèves peuvent acquérir l’habileté à diviser un ensemble d’éléments en parties équivalentes. Par la suite, elles et ils peuvent vivre des expériences qui font appel à des schèmes de pensée plus élaborés dans lesquels un seul élément est fractionné (par exemple, la division d’un carton en trois parties équivalentes pour faire un bricolage).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 58.
Dans cette vidéo, les élèves représentent le quart du tout à l’aide des modèles de surface et de longueur.
 Description de la vidéo
Description de la vidéo
Description à venir
Connaissance : nombre fractionnaire
L’apprentissage des fractions débute généralement avec l’utilisation de fractions propres, soit des fractions inférieures à 1. En 2e année, les élèves rencontrent des fractions qui représentent des quantités supérieures à 1 (par exemple, en comptant des morceaux de tartes coupées en quarts, on peut compter 11 quarts qui restent). De telles situations amènent les élèves aux nombres fractionnaires (par exemple, 2 et \(\frac{3}{4}\)).
Exemple
Si l’on a \(2 \frac{3}{4} \) tartes, on peut couper les 2 tartes en quarts, ce qui fait 8 quarts. Si l’on ajoute les 3 autres quarts, on obtient un total de 11 quarts, ou \(\frac{11}{4}\).
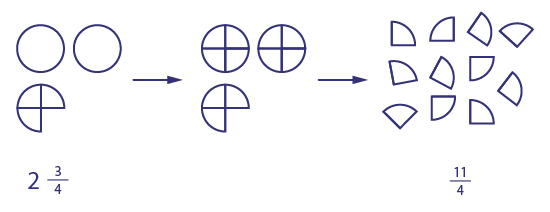
Le premier ensemble est constitué de deux cercles et de trois quarts d’un cercle. En dessous, il est écrit « deux et trois quarts ». Le deuxième ensemble est constitué de deux cercles divisés en quatre parties égales et de trois quarts d’un cercle. Le troisième ensemble est constitué d’onze quarts de cercles en pièces détachées. En dessous, il est écrit « onze quarts ».
Si l’on a 11 quarts de tartes, on peut grouper les quarts de tartes, 4 à la fois, pour former des tartes entières. On peut ainsi former 2 tartes avec 8 morceaux. Il reste alors 3 quarts. On a donc 2 et \(\frac{3}{4}\) tartes.
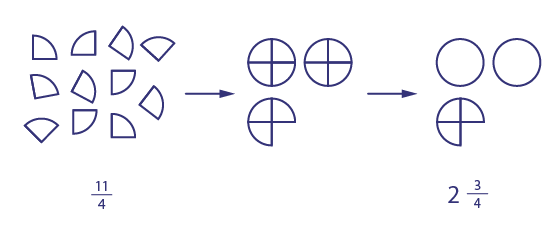
Le premier ensemble est constitué d’onze quarts de cercles en pièces détachées. En dessous, il est écrit « onze quarts ». Le deuxième ensemble est constitué de deux cercles divisés en quatre parties égales et de trois quarts d’un cercle. Le troisième ensemble est constitué de deux cercles et de trois quarts d’un cercle. En dessous, il est écrit « deux et trois quarts ».
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 53 et 54.
Connaissance : fraction
La compréhension de la représentation de quantités par des fractions permet d’approfondir le concept de quantité. Il importe de comprendre que les fractions (par exemple, un demi, un tiers, un quart) représentent des quantités différentes selon qu’elles font référence à une partie d’un tout (une longueur, une surface ou un solide) ou à une partie d’un ensemble. Par exemple, un tiers d’une tablette de chocolat (partie d’un tout) représente une quantité de chocolat en fonction de la grosseur de la tablette originale. Cependant, un tiers d’une douzaine d’œufs (partie d’un ensemble) représente quatre œufs.

Au-dessus du premier morceau de chocolat à gauche, qui contient trois carrés, il est écrit : « Parties d’un tout ». Une flèche au troisième carré mentionne la fraction un tiers. Au centre, il y a un morceau de chocolat à trois carrés. Le carré du bas possède une flèche qui mentionne la fraction un tiers. Et à droite, il y a une douzaine d’œufs dont les quatre derniers œufs à droite sont encerclés. Une flèche part de l’ensemble de quatre et mentionne la fraction un tiers. Et au-dessus des œufs, il est écrit : « Partie d’un ensemble ».
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 48.
Fournir aux élèves des occasions de découvrir que :
- lorsque la fraction représente une région (modèle de surface), l’aire de chaque partie doit être de mesure équivalente;
- lorsque les fractions sont utilisées pour décrire des ensembles (modèle d’ensemble), les objets composant les ensembles peuvent être de tailles différentes (par exemple, si l’on dit que \(\frac{1}{2}\) du bol de fruits est composé de pommes, l’autre \(\frac{1}{2}\) peut être composé de raisins qui ont une taille inférieure aux pommes);
- la fraction représente une relation plutôt qu’un nombre particulier. Il importe que les élèves sachent que \(\frac{1}{2}\) d’une petite quantité peut être beaucoup plus petit que \(\frac{1}{3}\) d’une grande quantité;
- la fraction représente une partie d’un tout.
Source : Guide d'enseignement efficace des mathématiques, de la 1re à la 3e année, p. 30.
Connaissance : partage équitable
Situation où un ensemble est partagé ou distribué parmi un nombre connu de personnes ou de groupes.
Exemple
Sacha a 12 pommes. Il veut les partager également entre 4 amis. Combien de pommes chaque ami recevra-t-il?
Note : Plusieurs élèves commencent par distribuer des objets entiers, puis séparent ceux qui restent. D’autres séparent chaque élément et distribuent les parties. Lorsque le nombre de personnes est supérieur au nombre d’objets à partager, il faut diviser les objets dès le début du processus de partage.
Un demi : Lorsqu’un tout est divisé en 2 parties équivalentes, chaque partie est la moitié de la quantité originale. Deux demis donnent un tout.
Un quart : Lorsqu’un tout est partagé en 4 parties équivalentes, chaque partie représente 1 quart de la quantité originale. Quatre quarts donnent un tout.
Un tiers : Lorsqu’un tout est partagé également en 3 parties, chaque partie représente 1 tiers du tout. Trois tiers forment un tout.
Un sixième : Lorsqu’un tout est partagé également en 6 parties, chaque partie représente 1 sixième du tout. Six sixièmes forment un tout.
