B1.6 Use drawings to represent, solve, and compare the results of fair-share problems that involve sharing up to 10 items among 2, 3, 4, and 6 sharers, including problems that result in whole numbers, mixed numbers, and fractional amounts.
Skill: Representing and Solving Fair-Share Problems
In the primary grades, students have the opportunity to explore fractions by sharing sets of objects (for example, if 3 friends want to share 18 apples equally, each will receive one third of the apples) and by examining whole parts separated into equivalent parts (for example, a rectangle separated into fourths). Partitioning can then serve as a springboard for the study of fractions in the junior grades. Note that in grade 2 , the curriculum limits the study of fractions to halves, thirds, fourths and sixths.
By continuing to build on the principle of division, students create connections between the action of division, the whole and the parts of the whole. They are then able to better understand fraction notation and develop a sense of fraction. Students understand that the fraction is also used to illustrate a remainder after sharing (for example, if 4 students want to share 5 cupcakes, each gets 1 cupcake and one fourth of a cupcake).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 28.
Exploration of Fractions
Baroody and Coslick (Fostering Children's Mathematical Power: An Investigative Approach to K-8 Mathematics Instruction, 1998, pp. 9-14 and 9-15) advocated that a "meaningful approach" to learning fractions follows a progression that moves students from informal, concrete representations to formal, abstract representation. The first step in this progression is the sharing of quantities.
Sharing
Any activity that engages students in a meaningful experience of sharing, without explicit reference to terminology or symbolism, provides them with a concrete foundation for understanding the concept of fraction. Beginning with a common everyday task (for example, sharing felt pens or crayons for an art project), students can develop the ability to divide a set of items into equivalent parts. Later, they may have experiences that involve more sophisticated thinking in which a single item is split (for example, dividing a cardboard box into three equivalent parts to make a craft).
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 58.
Knowledge: Mixed Numbers
Learning about fractions usually begins with proper fractions, which are fractions less than 1. In Grade 2 , students encounter fractions that represent quantities greater than 1 (for example, counting pieces of pie cut into fourths, there are 11 fourths left). Such situations lead students to mixed numbers (for example, 2 and 3 one fourths).
Example
If you have 2 pies, you can cut the 2 pies into fourths, making 8 fourths. Adding the other 3 fourths gives a total of 11 fourths, or \(\frac{11}{4}\).

If you have 11 fourths of pie, you can group the fourths, 4 at a time, to form whole pies. This way you can form 2 pies with 8 pieces. This will leave 3 fourths. So we have \(2\frac{3}{4}\) pies.
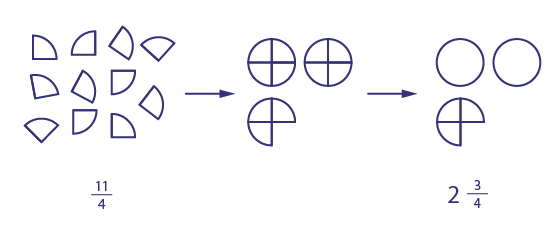
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 2, Fractions, p. 53 et 54.
Knowledge: Fraction
Understanding the representation of quantities by fractions deepens the concept of quantity. It is important to understand that fractions (for example, one-half, one-third, one-fourth) represent different quantities depending on whether they refer to a part of a whole (a length, an area, or a solid) or to a part of a set. For example, one third of a chocolate bar (part of a whole) represents a quantity of chocolate based on the size of the original bar. However, one third of a dozen eggs (part of a set) represents four eggs.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 48.
Provide opportunities for students to discover that:
- when the fraction represents an area (area model), the area of each part must be of equivalent size;
- when fractions are used to describe sets (set model), the objects making up the sets may be different sizes (for example, if the fruit bowl is said to be made up of apples, the other fruit bowl may be made up of grapes that are smaller than the apples);
- the fraction represents a relationship rather than a particular number. It is important for students to know that half of a small amount can be much smaller than one third of a large amount;
- the fraction represents a part of a whole.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, Document d'appui, p. 30.
Knowledge: Fair-Sharing
A situation where a whole or a set is shared or distributed among a known number of people or groups.
Example
Sacha has 12 apples. He wants to share them equally among 4 friends. How many apples will each friend get?
Note: Some students will begin by distributing whole objects, then partitioning the remaining ones. Others partition each whole and distribute the parts. Support students to recognize that when the number of people is greater than the number of objects to be shared, the objects must be divided from the start of the sharing process.
Half: When a whole is divided into 2 equivalent parts, each part is half of the original quantity. Two halves make a whole.
One fourth: When a whole is divided into 4 equivalent parts, each part represents 1 fourth of the original quantity. Four fourths make a whole.
One third: When a whole is divided equally into 3 parts, each part represents 1 third of the whole. Three thirds form a whole.
One sixth: When a whole is divided equally into 6 parts, each part represents 1 sixth of the whole. Six sixths form a whole.
