B2.3 Utiliser des stratégies de calcul mental, y compris l’estimation, pour additionner des nombres naturels dont la somme est égale ou inférieure à 50 et pour soustraire des nombres égaux ou inférieurs à 50, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental
La résolution de problèmes à l’aide du calcul mental est souvent un bon moyen d’inciter les élèves à élaborer des manières plus efficientes de faire des calculs papier-crayon. Le personnel enseignant peut encourager les élèves à recourir au calcul mental en leur présentant les équations horizontalement \(34 + 16\) plutôt que verticalement :
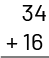
Les élèves qui prennent le temps d’observer les nombres et de penser à la meilleure façon de résoudre l’équation avant de commencer à faire quoi que ce soit sur papier sont plus susceptibles de choisir la méthode la plus efficiente pour résoudre l’équation. Un moment de réflexion, par exemple, avant de calculer \(19 + 21\) peut les aider à se rendre compte qu’il est très facile de combiner le 1 et le 19 pour faire 20, puis d’ajouter le 20 qui reste pour arriver à la réponse, soit 40. Devant un calcul, les élèves utilisent souvent, mais pas toujours, des stratégies souples dans leur tête et prennent, au besoin, quelques notes écrites pour visualiser leur cheminement.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 40 et 41.
Habileté : développer et utiliser des stratégies liées au dénombrement, à la valeur de position et à la décomposition
L’habileté des élèves à développer et à utiliser des stratégies liées au dénombrement, à la valeur de position et à la décomposition leur permet d’effectuer les opérations arithmétiques avec efficacité.
L’utilisation par les élèves de diverses stratégies liées au dénombrement (par exemple, décomposition, regroupement) leur permet d’effectuer les opérations arithmétiques de base avec efficacité et de mieux en comprendre le sens. Les élèves sont, par exemple, en mesure d’effectuer des calculs simples lorsqu’elles et ils réussissent à passer de « compter tout » à « compter à partir de » (par exemple, pour calculer \(22 + 4\), au lieu de compter tous les jetons jusqu’à 22, puis d’en ajouter 4, l’élève commence à compter à partir de 22 en disant « 23, 24, 25, 26 »). Les élèves peuvent aussi apprendre à utiliser efficacement la décomposition et le regroupement des nombres pour additionner deux quantités. Ainsi, pour additionner 38 et 5, elles et ils peuvent décomposer 5 de manière à obtenir 2 et 3, regrouper ensuite 2 et 38 afin de former quatre dizaines et enfin additionner le 3 qui reste pour arriver à 43. Les stratégies liées à la décomposition en fonction des valeurs de position sont aussi fort utiles. Les élèves peuvent, par exemple, additionner 16 et 23 en décomposant d’abord les deux nombres en dizaines et en unités (\(10 + 20 = 30\); \(6 + 3 = 9\); \(30 + 9 = 39\)). Les élèves peuvent aussi avoir recours à une stratégie liée aux doubles; par exemple, pour déterminer la somme de 26 et de 25, elles et ils peuvent décomposer 26 de manière à obtenir 25 et 1, puis additionner 25 et 25 pour obtenir 50 (les élèves savent que deux pièces de monnaie de 25 ¢ donnent 50 ¢) et ajouter ensuite le 1 qui reste pour arriver à 51.
Lorsque les élèves connaissent bien toutes les façons de décomposer les nombres jusqu’à 10, elles et ils peuvent effectuer les additions et les soustractions de nombres inférieurs à 20 qui ne nécessitent pas de regroupements (par exemple, \(10 + 4\), \(11 + 6\), \(15 - 5\) ou \(16 - 3\)). Ensuite, les élèves peuvent passer aux additions et aux soustractions de nombres inférieurs à 20 qui requièrent un regroupement (par exemple, \(13 + 8\), \(17 - 9\)). Ces stratégies sont aussi utilisées avec les nombres inférieurs à 50 (par exemple, pour calculer \(33 + 8\), l’élève décompose 8 en 7 et 1, puisqu’elle ou il sait qu’il faut 7 pour se rendre à la prochaine dizaine. Elle ou il additionne \(33 + 7\) qui donne 40, puis \(40 + 1\), ce qui est égal à 41).
Plusieurs sources (Carpenter et coll., 1998; Fuson et coll., 1997; Kamii et Dominick, 1998) indiquent que les élèves acquièrent une compréhension approfondie du sens des opérations et de la valeur de position si on leur offre le soutien et les occasions nécessaires pour élaborer leurs propres stratégies de résolution de problèmes de numération. De fait, les élèves sont en mesure de trouver des façons très efficaces d’effectuer des calculs mentaux complexes tels que \(13 + 29\). Elles et ils peuvent, par exemple, choisir de faire des dizaines, comme cela est illustré ci-dessous.
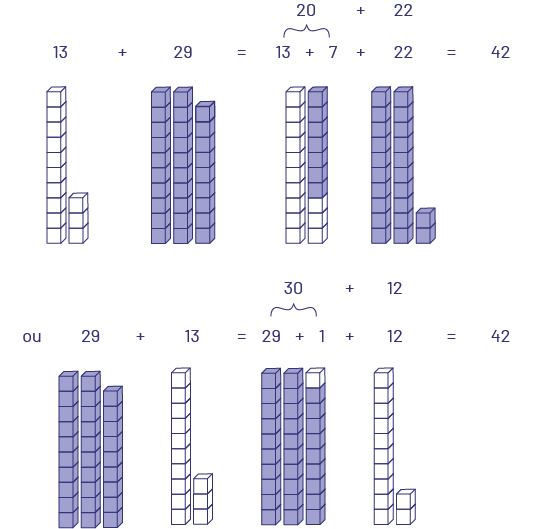
Première équation : 13 plus 29 égale 13 plus sept plus 22 égale 42. Sous le treize, il y a une tour de 10 unités blanches et une tour de trois unités blanches. Sous le 29, il y a deux tours de dix unités violettes et une tour de neuf unités violettes. Au-dessus de 13 plus sept, il y a une accolade qui dit : vingt. Et en dessous, il y a une tour de dix unités blanches et une tour de sept unités violettes et de trois unités blanches. Au-dessus de 22, il est écrit « plus 22 ». En dessous, il y a deux tours de dix unités violettes et une tour de deux unités violettes. Deuxième équation : ou 29 plus treize égale 29 plus un plus douze égale 42. Sous le 29, il y a deux tours de dix unités violettes et une tour de neuf unités violettes. Sous le 13, il y a une tour de 10 unités blanches et une tour de trois unités blanches. Au-dessus de 29 plus un, il y a une accolade qui dit : trente. Sous 29 plus un, il y a deux tours de dix unités violettes et une tour de neuf unités violettes et d’une unité blanche. Au-dessus du douze, il est écrit « plus douze ». Et sous le douze, il y a une tour de dix unités blanches et une tour de deux unités blanches.
Les élèves qui n’ont pas été amenés à développer de telles stratégies s’en remettent presque toujours automatiquement à l’algorithme usuel de l’addition. Plusieurs peuvent l’utiliser correctement, alors que d’autres commettent des erreurs et obtiennent une réponse erronée, comme cela est illustré ci-dessous.
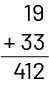
Pour déterminer la somme de 19 et de 33, des élèves additionnent 9 et 3, et écrivent 12, puis additionnent 1 et 3, et écrivent 4. Elles et ils donnent donc comme réponse 412, sans se rendre compte de l’invraisemblance de la réponse.
Cependant, les élèves qui ont développé certaines stratégies de calcul mental reconnaissent que cette réponse est invraisemblable, puisque l’addition des dizaines donne 40; la réponse doit donc être près de ce nombre et ne peut pas être un nombre aussi grand que 412.
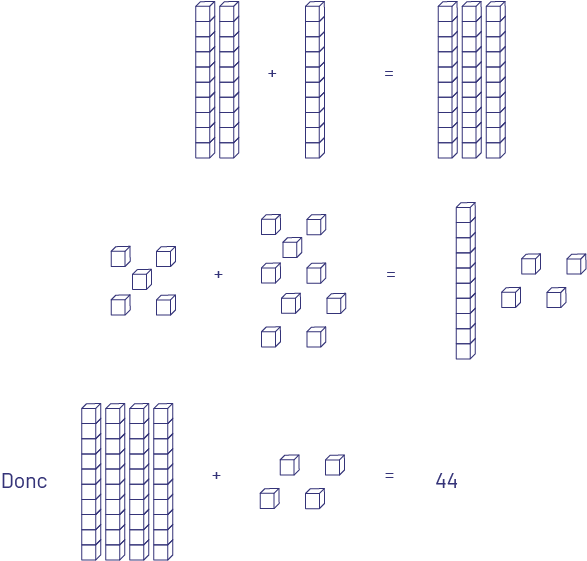
Les élèves doivent aussi avoir de nombreuses occasions de modéliser les opérations arithmétiques et d’utiliser diverses stratégies. Une ou un élève, par exemple, peut modéliser la solution de l’addition de 25 et de 19 en utilisant le matériel de base dix comme suit : combiner 2 languettes et 1 languette, puis combiner 5 cubes d’unité et 9 cubes d’unité et les remplacer par 1 languette et 4 cubes d’unité, ce qui donne 4 languettes et 4 cubes d’unité (44).
Il est donc important d’offrir aux élèves de nombreuses occasions de faire des expériences leur permettant de se familiariser avec les stratégies pour apprendre les faits numériques de base relatifs à l’addition et à la soustraction, pour que celles-ci deviennent des stratégies de calcul mental.
Les élèves peuvent ensuite utiliser une grille de nombres pour modéliser la solution de l’addition de 13 et de 37 en procédant comme suit : commencer à 13 sur la grille, descendre de 3 cases jusqu’à 43, puis se déplacer de 7 cases vers la droite jusqu’à 50.

Une grille numérotée dix par dix présente tous les nombres d’un à cent, sauf le nombre vingt, qui est absent. Les cases des nombres 13 et 50 sont colorées de violet. À partir du nombre 13 jusqu’au nombre 43 en descendant, puis de 43 jusqu’à 50 en allant vers la droite, des flèches relient chaque nombre au suivant. Sous la grille, il est écrit : 13 plus 37 égale cinquante.
\(13 + 37 = 50\)
L’utilisation de matériel de base dix et la grille de nombres sont deux stratégies différentes aussi valables l’une que l’autre, pourvu que les élèves soient capables d’expliquer leur raisonnement. Les élèves qui peuvent résoudre des problèmes comme ceux qui précèdent de manières variées comprennent mieux la façon d’utiliser les algorithmes usuels parce qu’elles et ils sont davantage en mesure de saisir la façon dont les différentes étapes de l’algorithme agissent sur les nombres. De plus, les occasions de modéliser des opérations arithmétiques aident les élèves à effectuer mentalement des opérations comportant des nombres à deux chiffres, sans devoir recourir à un crayon et à du papier.
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 26-30.
Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec la soustraction.
 Description de la vidéo
Description de la vidéo
Description à venir
Les modèles aident les élèves à établir des relations et ainsi à mieux comprendre ce que les symboles représentent dans les opérations. Le personnel enseignant peut aider les élèves à relier leur compréhension du problème d’abord avec du matériel de manipulation, puis avec des symboles comme les signes =, + et –, pour ensuite calculer mentalement.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 14.
L’estimation
L’estimation est une habileté importante associée aux opérations sur les nombres à plusieurs chiffres. Cette habileté aide les élèves à développer leur sens du nombre et à l’utiliser pour comprendre chacune des étapes des algorithmes usuels.
Le but de l’estimation n’est pas d’arriver à une réponse exacte, mais à une approximation logique. Des questions comme « La réponse est-elle moins que 25? plus que 10? » aident les élèves à reconnaître les possibilités et à évaluer la vraisemblance de leurs réponses. L’enseignante ou l’enseignant peut utiliser les stratégies présentées ci-dessous pour aider les élèves à développer l’habileté à estimer. Il faut éviter d’enseigner ces stratégies comme des termes et des démarches à mémoriser ou à utiliser constamment. L’enseignante ou l’enseignant peut s’en servir pour aider les élèves à mieux comprendre ce qu’elles et ils font et la raison pour laquelle elles et ils le font. Les stratégies peuvent être présentées aux élèves uniquement lorsque l’occasion se présente. Il ne faut donc pas s’attendre à ce que les élèves utilisent toutes ces stratégies, du moins pas avant les dernières années d’études du cycle primaire.
En 2e année, les élèves peuvent utiliser les stratégies d’estimation suivantes :
- Le regroupement
- Le regroupement est utile lorsque les nombres sont plus faciles à calculer. Le regroupement permet d’effectuer une addition répétée.
- Les nombres pratiques
- La stratégie des nombres pratiques consiste à utiliser les nombres qui sont faciles à manier. Dans l’addition et la soustraction, les élèves cherchent les nombres dont la somme ou la différence est près de 10.
Bien des élèves ne saisissent pas l’importance et la pertinence de l’estimation. Elles et ils croient que l’estimation est une façon d’arriver à la réponse exacte, de sorte qu’il leur semble nécessaire de changer leur estimation après avoir effectué un calcul précis. En offrant chaque jour aux élèves de nombreuses occasions de s’exercer à estimer, on peut les aider à améliorer cette habileté, à développer leur sens de l’estimation et à comprendre l’utilité de l’estimation dans la vie quotidienne.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, 68-70.
