B2.3 Use mental math strategies, including estimation, to add and subtract whole numbers that add up to no more than 50, and explain the strategies used.
Skill: Using Mental Math Strategies
Problem solving using mental math is often a good way to encourage students to develop more efficient ways of doing paper-and-pencil calculations. Teachers can encourage students to use mental math by presenting equations horizontally (34 + 16) rather than vertically:
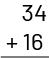
Students who take the time to look at the numbers and think about the best way to solve the equation before they start doing anything on paper are more likely to choose the most efficient way to solve the equation. A moment of reflection, for example, before calculating \(19 + 21\) can help them realize that it is very easy to combine the 1 and 19 to make 20, and then add the remaining 20 to arrive at the answer, 40. When faced with a calculation, students often, but not always, use flexible strategies in their heads and make a few written notes, if necessary, to visualize their path.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 40-41.
Skill: Develop and Use Strategies Related to Counting, Place Value and Decomposition
Students' ability to develop and use strategies related to counting, place value, and decomposition enables them to perform mathematical operations effectively.
Young students depend on their counting strategies to help them make sense of addition and subtraction. Moving from the counting-all stage to the counting-on stage helps them do simple computations (for example, when adding 22 and 4, rather than counting all the counters for 22 and then for 4, they count on from 22: 23, 24, 25, 26). Students also need to develop a flexible approach to combining and partitioning numbers in order to fully understand the operations of addition and subtraction. This flexible approach to combining and partitioning numbers involves knowing that two quantities, such as 38 objects and 5 objects, can be combined by partitioning 5 into 2 and 3, combining the 2 with 38 to make four tens, and adding the 3 remaining to make 43. Using a flexible approach also involves, for example, combining 16 objects and 23 objects by partitioning both numbers into their respective tens and ones, combining the tens (10 + 20 = 30), combining the ones (6 + 3 = 9), and then combining the tens with the ones (30 + 9 = 39). Another student might solve the same problem by decomposing 26 into 25 and 1, adding the two 25’s to make 50 (because they know that two quarters make 50 cents), and then adding the 1 remaining to make 51.
Once students know all the combinations of numbers to 10, they are prepared to work with numbers less than 20 that do not require regrouping (for example, 10 + 4, 11 + 6, 15 – 5, 16 – 3). After this, they can work with numbers less than 20 that do require regrouping (for example, 13 + 8, 17 – 9), and having developed this valuable regrouping concept, they can extend it to all other numbers less than 50 (for example, to calculate 33 + 8, the student decomposes 8 into 7 and 1, since they know that it takes 7 to get to the next ten. They add 33 + 7, which gives 40, then 40 + 1 which equals 41.
There is significant evidence (Carpenter et al., 1998; Fuson et al., 1997; Kamii &Dominick, 1998) that children develop an enhanced understanding of computations and the place value system if they are given the opportunities and support to develop their own strategies for solving number problems. When children couple their emerging computational strategies with an understanding of base ten grouping (also called unitizing), they develop very efficient ways of using their understanding of place value to mentally calculate complex computations, such as (13 + 29). For example, they may choose to make tens, as illustrated below.
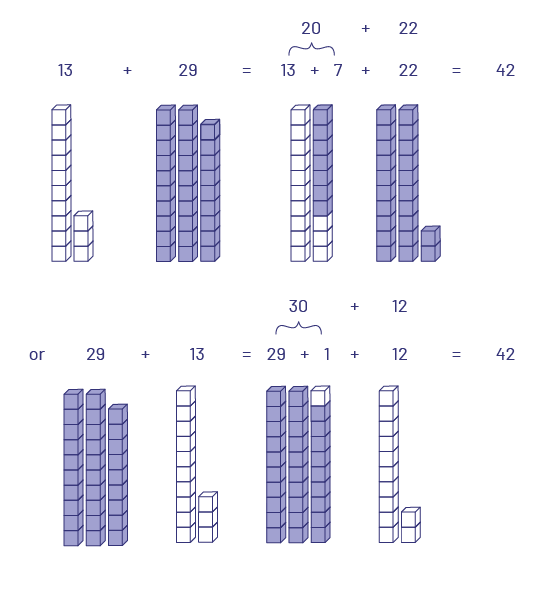
Students who have not been taught to develop such strategies almost always automatically rely on the standard addition algorithm. Many may use it correctly, while others make mistakes and get the wrong answer, as illustrated below.
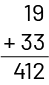
To determine the sum of 19 and 33, students add 9 and 3, and write 12, then add 1 and 3, and write 4. They therefore give as an answer 412, without realizing the implausibility of the answer.
However, students who have developed some mental math strategies recognize that this answer is implausible, since adding the tens gives 40; therefore, the answer must be close to that number and cannot be a number as large as 412.
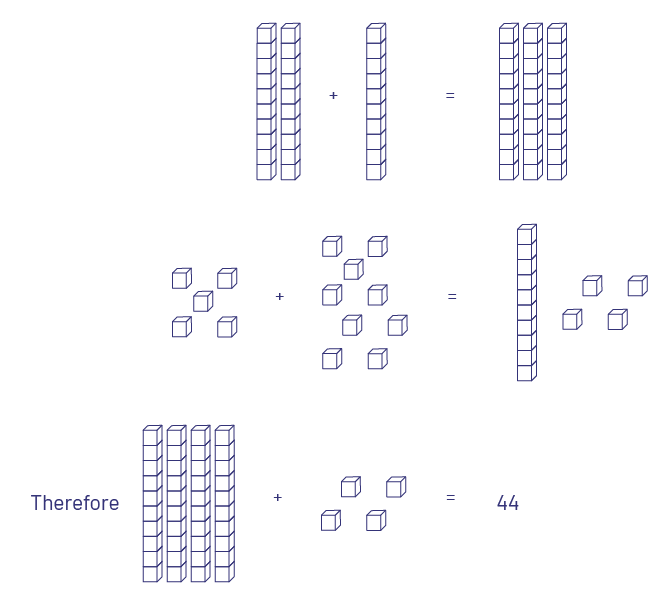
Students should also have many opportunities to model mathematical operations and use a variety of strategies. A student, for example, can model the solution to the addition of 25 and 19 using base ten materials as follows: combine 2 rods and 1 rod, then combine 5 unit cubes and 9 unit cubes and replace them with 1 rod and 4 unit cubes, resulting in 4 rods and 4 unit cubes (44).
Therefore, it is important to provide many opportunities for students to have experiences that allow them to become familiar with strategies for learning basic addition and subtraction facts, so that these become mental computational strategies.
Students can then use a number chart to model the solution to the addition of 13 and 37 by doing the following: start at 13 on the grid, move down 3 spaces to 43, and then move 7 spaces to the right to 50.

\(13 + 37 = 50\)
The use of base ten materials and the number chart are two different strategies that are equally valid, as long as students are able to explain their reasoning. Students who can solve problems like the above in a variety of ways have a better understanding of how to use standard algorithms because they are better able to understand how the different steps in the algorithm affect the numbers. In addition, opportunities to model mathematical operations help students mentally perform operations involving two-digit numbers without the need for pencil and paper.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 26-30.
Models help students make connections and thus gain a better understanding of what the symbols represent in operations. Teachers can help students connect their understanding of the problem first with manipulatives and then with symbols such as =, +, and - signs, and then calculate mentally.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 14..
Estimation
Estimation is an important skill associated with operations on multi-digit numbers. This skill helps students develop their number sense and use it to understand each step of standard algorithms.
The goal of estimation is not to arrive at an exact answer, but rather for a logical approximation. Questions such as "Is the answer less than 25? more than 10?" and so on help students recognize possibilities for the answer and assess the reasonableness of their answers. The teacher can use the strategies outlined below to help students develop the skill of estimating. These strategies should not be taught as terms and procedures to be memorized or used constantly. The teacher can use them to help students better understand what they are doing and why they are doing it. Strategies should be introduced to students only when the opportunity arises. Therefore, students should not be expected to use all of these strategies, at least not until the later grades of the Primary Division.
In Grade 2 , students may use the following estimation strategies:
- Clustering: Combining is useful when numbers are close to each other. Clustering allows for repeated addition.
- Nice Numbers: The compatible number strategy involves using numbers that are easy to work with. In addition and subtraction, students look for numbers whose sum or difference is close to a multiple of 10.
Many students do not understand the importance and relevance of estimation. They believe that estimating is a way to arrive at the correct answer, so they find it necessary to change their estimation after making an accurate calculation. Providing students with many opportunities to practice estimating each day can help them improve this skill, develop their sense of estimation, and understand the usefulness of estimation in everyday life.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 68-70.
