B2.6 Représenter et résoudre des problèmes relatifs à la division de 12 éléments ou moins en tant que partage égal d’une quantité, à l’aide d’une variété d’outils et de schémas.
Habileté : représenter et résoudre des problèmes relatifs à la division
Au début, les élèves ont habituellement besoin de modéliser les faits en utilisant leurs doigts ou des objets. Elles et ils utilisent la stratégie de dénombrement nouvellement acquise pour trouver la réponse à un problème tel que : « Jeanne a 3 pommes et on lui en donne 2 de plus. Combien en a-t-elle maintenant? » Les élèves devront peut-être compter 3 jetons, puis 2 autres jetons, puis recompter tous les jetons ensemble à partir du premier pour arriver au total de 5 jetons.
Dans le cas de la multiplication ou de la division, les élèves modélisent ces opérations au moyen d’objets, de traits de dénombrement ou de dessins pour représenter des objets organisés par groupes pour ensuite dénombrer ces objets afin de trouver une réponse. Elles et ils utilisent ces modèles afin de trouver une solution à des problèmes tels que : « Trois bols contiennent des pommes. Chaque bol contient 5 pommes. Combien y a-t-il de pommes en tout? » Les élèves pourront dessiner les bols de pommes et dénombrer les pommes dessinées afin de déterminer le nombre total de pommes.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 12.
Pour aborder la division, les élèves doivent comprendre d’autres concepts mathématiques. Elles et ils doivent notamment savoir que la division peut s’interpréter comme une soustraction répétée. Elles et ils doivent aussi être en mesure de créer des groupes ou des ensembles de taille égale et de séparer des quantités en groupes ou en ensembles égaux.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 8.
Effets des opérations
Chaque opération produit un effet sur les quantités en cause. Selon l’opération, certaines quantités augmentent ou diminuent. Elles peuvent augmenter ou diminuer de beaucoup ou de peu. Suivre l’effet des opérations sur les nombres permet aux élèves d’établir des liens entre les opérations et d’anticiper le résultat d’une opération. Si, par exemple, on soustrait 8 de 160, on remarquera peu d’effet, car la différence entre 160 et 152 est relativement petite. Cependant, si l’on divise 160 par 8, l’effet produit est grand, car le quotient obtenu, soit 20, est beaucoup plus petit que 160.
Une mise en garde s’impose : il faut faire preuve de prudence lorsqu’on généralise, car les opérations sur les nombres décimaux ou les fractions peuvent avoir des effets différents que les effets sur les nombres naturels. Dans certains cas, l’effet peut même être l’inverse.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 90 et 91.
Dans la division, une quantité est séparée en groupes égaux. Le dividende représente la quantité à partager, alors que le diviseur et le quotient représentent respectivement le nombre de groupes et la taille des groupes si la division a le sens de partage ou, l’inverse, si la division a le sens de groupement.
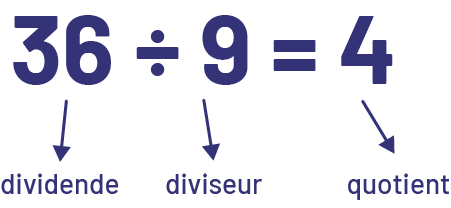
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 81.
Dans les problèmes présentés aux élèves, on associe trop souvent la division à un seul sens, soit le partage. Le sens de groupement est habituellement négligé. La division a un sens de partage lorsque la quantité totale et le nombre de groupes sont connus (par exemple, 3 élèves veulent se partager équitablement 15 pommes et l’on cherche le nombre de pommes que chaque personne recevra).
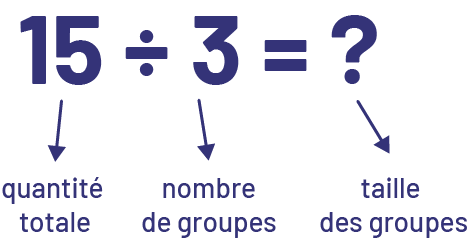
La division a un sens de groupement lorsque la quantité totale et le nombre d’éléments dans chaque groupe (taille des groupes) sont connus (par exemple, on a 15 pommes et on veut les mettre dans des sacs, soit 3 pommes par sac; on cherche le nombre de sacs nécessaire).
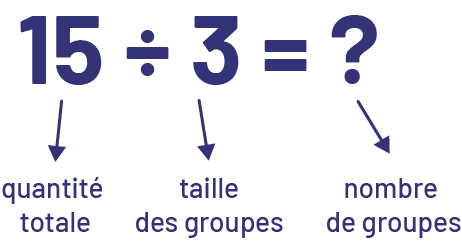
L’équation suivante est présentée : 15 divisé par trois égale point d’interrogation. Sous le nombre 15, il est écrit « quantité totale ». Sous le chiffre trois, il est écrit « taille des groupes ». Et sous le point d’interrogation, il est écrit « nombre de groupes ».
Il est essentiel de traiter des deux types de problèmes, puisqu’ils sont la base de l’intégration d’autres concepts mathématiques. Il n’est pas nécessaire que les élèves sachent les noms des types de problèmes, mais il est essentiel qu’elles et ils aient l’occasion de résoudre des problèmes des divers types, tout en employant une variété de stratégies.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 86.
Problèmes écrits relatifs à la division
Les élèves acquièrent une bonne compréhension de la division ainsi que des relations entre les nombres en résolvant des problèmes écrits. Les types de problèmes présentés ci-dessous, au moyen d’exemples, peuvent aider les élèves à percevoir les faits numériques de base relatifs à la division de diverses façons, selon qu’il s’agit de problèmes de groupes égaux ou d’arrangements. Le recours aux problèmes pour présenter les faits numériques de base oblige les élèves à raisonner pour trouver des solutions, ce qui leur permet de développer un meilleur sens des opérations.
Les exemples de problèmes écrits ci-dessous contiennent des nombres composés d’un chiffre. Les structures des deux types de problèmes écrits se prêtent aussi aux nombres à plusieurs chiffres.
Problèmes de groupes égaux
- Groupes égaux : Taille des groupes inconnue (partage)
- Julie a 10 livres. Elle veut les donner à 5 de ses camarades. Combien de livres chaque camarade recevra-t-il?
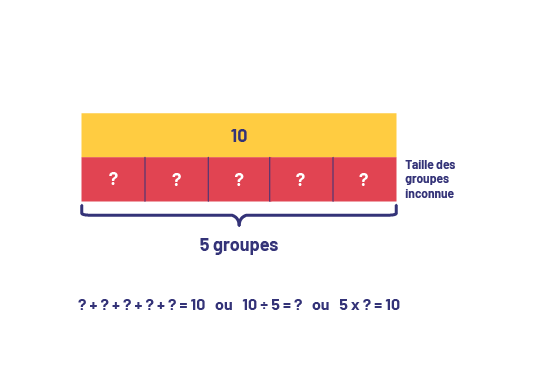
Une réglette orange repose sur cinq plus petites réglettes rouges toutes de taille identique, ce qui forme un rectangle. Sur la réglette orange, il y a un le nombre dix. Sur chaque réglette rouge, il y a un point d’interrogation. À côté des réglettes rouges, il est écrit « taille des groupes inconnue ». En dessous des réglettes, une accolade dit : « cinq groupes ». Au bas, il est écrit : pont d’interrogation plus point d’interrogation, plus point d’interrogation plus point d’interrogation plus point d’interrogation égale dix ou cinq multiplié par point d’interrogation égale dix.
- Groupes égaux : Nombre de groupes inconnu (groupement)
- Julie a acheté 10 livres pour ses camarades et prépare des sacs-cadeaux. Elle met 2 livres dans chaque sac-cadeau. Combien de sacs-cadeaux Julie a-t-elle utilisés?
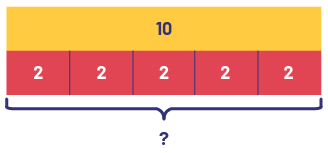
Une réglette orange repose sur cinq plus petites réglettes rouges toutes de taille identique, ce qui forme un rectangle. Sur la réglette orange, il y a un le nombre dix. Sur chaque réglette rouge, il y a le chiffre deux. En dessous, une accolade indique un point d’interrogation.
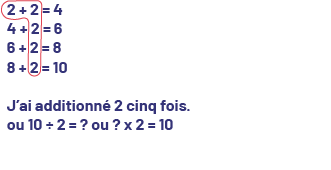
Les équations suivantes sont placées l’une sous l’autre : deux plus deux égale quatre. Quatre plus deux égale six. Six plus deux égale huit. Huit plus deux égale dix. Tous les chiffres deux sont entourés ensemble au crayon rouge pour les regrouper. En dessous, il est écrit : « J’ai additionné deux cinq fois. Ou dix divisé par deux égale point d’interrogation ou point d’interrogation multiplié par deux égale dix ».
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10 et 11.
