B2.6 Represent division of up to 12 items as the equal sharing of a quantity, and solve related problems, using various tools and drawings.
Skill: Representing and Solving Problems Related to Division
At first, students usually need to model facts using their fingers or objects. They use the newly acquired counting strategy to find the answer to a problem such as, "Jane has 3 apples and is given 2 more. How many does she have now?" Students may need to count 3 tokens, then 2 more tokens, then count all the tokens together again from the first token to arrive at a total of 5 tokens.
In the case of multiplication or division, students model these operations using objects, tally marks, or drawings to represent objects organized in groups and then count these objects to find an answer. They use these models to find a solution to problems such as: "Three bowls contain apples. Each bowl contains 5 apples. How many apples are there in total?" Students may draw the bowls and count the apples drawn to determine the total number of apples.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 12.
To address division, students need to understand other mathematical concepts. In particular, they need to know that division can be interpreted as repeated subtraction. They also need to be able to create groups or sets of equal size and to separate quantities into equal groups or sets.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 8.
Effect of Operations
Each operation has an effect on the quantities involved. Depending on the operation, certain quantities increase or decrease. They may increase or decrease by a lot or a little. Tracking the effect of operations on numbers allows students to make connections between operations and to anticipate the result of an operation. If, for example, 8 is subtracted from 160, little effect will be noticed because the difference between 160 and 152 is relatively small. However, if we divide 160 by 8, the product effect is large, because the resulting quotient, 20, is much smaller than 160.
One caveat is that care must be taken when generalizing, because operations on decimal numbers or fractions may have different effects than operations on whole numbers. In some cases, the effect may even be the opposite.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 90-91.
In division, a quantity is separated into equal groups. The dividend represents the quantity to be divided, while the divisor and quotient represent respectively the number of groups and the size of the groups if the division is partitive or, the opposite, if the division is quotative.
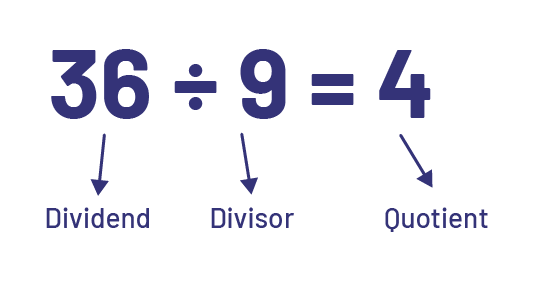
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 81.
In problems presented to students, division is too often associated with only one sense, namely equal-sharing (partitive division). The equal-grouping sense (quotative division) is usually neglected. Division has a partitive meaning when the total quantity and the number of groups are known (for example, 3 students want to share 15 apples equally and we are looking for the number of apples each person will receive).
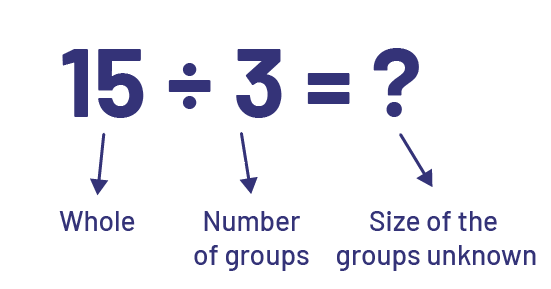
Division has a quotative meaning when the total quantity and the size of groups are known (for example, we have 15 apples and we want to put them in bags, 3 apples per bag; we look for the number of bags needed).
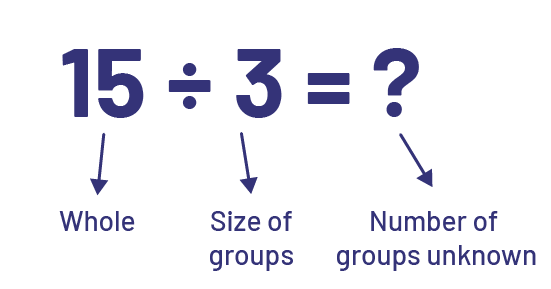
It is essential that both types of problems be addressed, as they are the basis for the integration of other mathematical concepts. It is not necessary for students to know the names of the problem types, but it is essential that they have the opportunity to solve problems of the various types, while employing a variety of strategies.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 86.
Written Problems Related to Division
Students develop an understanding of division as well as number relationships by solving written problems. The types of problems presented below, with examples, can help students see the basic division facts in a variety of ways, depending on whether the problems are partitive or quotative. Using problems to introduce basic number facts forces students to reason their way to solutions, which helps them develop a better sense of operations.
The written problem examples below contain single-digit numbers. The structures of both types of written problems also lend themselves to multi-digit numbers.
Equal-Sharing Division Problems (Partitive Division)
- Equal-Sharing: Group Size Unknown (Partitive Division) Julie has 10 books. She wants to give them to 5 of her classmates. How many books will each classmate receive?
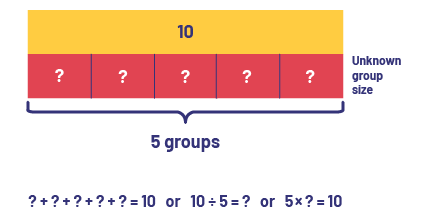
- Equal-Sharing: Number of Groups Unknown (Quotative Division) Julie has bought 10 books for her classmates and is making gift bags. She puts 2 books in each gift bag. How many gift bags did Julie use?
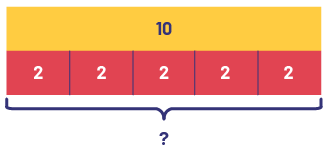
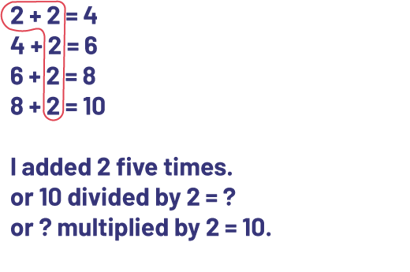
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10-11.