À vue d'oeil...

B1.7 Représenter et résoudre des problèmes de partage équitable ciblant la recherche et l’utilisation des fractions équivalentes, y compris des problèmes comportant des demis, des quarts et des huitièmes; des tiers et des sixièmes; ou des cinquièmes et des dixièmes.

Activité 1 : comparons des fractions (représenter et comparer des fractions)

---

Démarche

Demander à 6 élèves de se répartir en 2 groupes égaux.

Poser la question suivante :

• Quelle fraction chaque groupe représente-t-il?

Écrire cette fraction sur 2 cartons et demander à un ou à une élève de chaque groupe de la montrer.

• Combien d’élèves y a-t-il dans chaque demi?

Demander à 6 autres élèves de se répartir en 3 groupes égaux.

Poser la question suivante :

• Quelle fraction chaque groupe représente-t-il?

Écrire cette fraction sur 3 cartons et demander à un ou à une élève de chaque groupe de la montrer.

• Combien d’élèves y a-t-il dans chaque tiers?

Faire ressortir qu’il y a plus d’élèves dans le demi du 1^er groupe (3 élèves) que dans le tiers du 2^e groupe (2 élèves).

Demander à 6 élèves de se répartir en 2 groupes égaux.

Demander à 9 élèves de se répartir en 3 groupes égaux.

Procéder de la même façon que précédemment.

Faire ressortir qu’il y a le même nombre d’élèves dans le demi du groupe de 6 élèves et dans le tiers du groupe de 9 élèves, soit 3 élèves dans chaque groupe.

Demander à 6 élèves de se répartir en 2 groupes égaux.

Demander à 12 autres élèves de se répartir en 3 groupes égaux.

Procéder de la même façon que précédemment.

Faire ressortir qu’il y a moins d’élèves dans le demi du groupe de 6 élèves que dans le tiers du groupe de 12 élèves.

Refaire en comparant $\frac{1}{4}$ et $\frac{1}{2}$ de 20 jetons.

Note : Faire remarquer que la fraction unitaire ($\frac{1}{x}$ d’un ensemble) représente toujours 1 groupe d’un ensemble partagé en x groupes égaux, mais que la fraction d’un ensemble représente une quantité différente d’éléments selon le nombre d’éléments dans l’ensemble.

Intervention

Poursuivre le questionnement utilisé lors d’un enseignement explicite.

Source : Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, p. 56-57.

Activité 2 : la fête champêtre

---

Pour la fête champêtre, le personnel enseignant a organisé des jeux dans la cour d’école. Il y a une station de tapis glissants, où les élèves courent, prennent leur élan et glissent le plus loin possible sur un tapis plastifié mouillé. Pour l’analyse des résultats, le personnel enseignant a divisé la longueur des tapis en 5 ou en 10 sections égales.

Zoé glisse et le personnel enseignant affirme qu’elle a glissé sur une longueur de $\frac{2}{10}$ du tapis. Noah glisse et le personnel enseignant affirme qu’il a glissé sur une longueur de $\frac{2}{5}$ du tapis. Que remarques-tu? Qu’est-ce qui doit arriver pour que les 2 élèves glissent à distance égale?

Stratégie

Représentation de fractions équivalentes à l’aide d’un modèle de longueur

Voici les résultats de Zoé et de Noah.

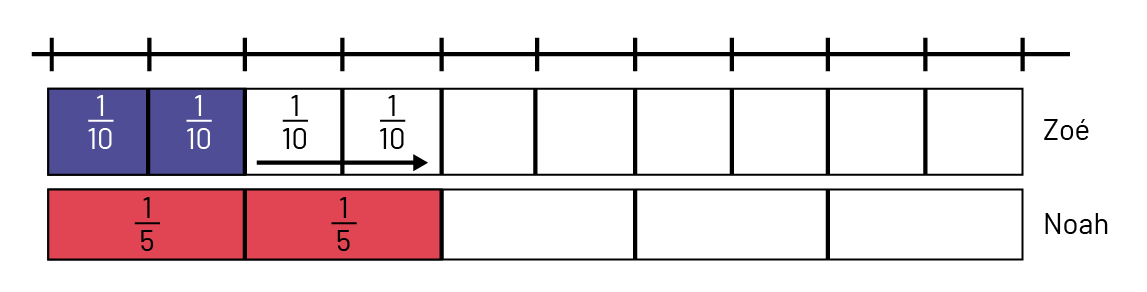Image Représentation de fractions équivalentes à l’aide d’un modèle de longueur. Une droite est divisée en dix parties égales. Sous la droite, il y a un tableau de dix cases de la même dimension que la droite, dans chaque case on peut lire la fraction, un dixième. Sous le premier tableau, il y a un deuxième tableau, ce dernier est divisé en 5 cases égales. Chaque case représente 2 cases du tableau précédent. On peut y lire la fraction un cinquième.

Je dessine $\frac{2}{10}$ du tout sur une bande fractionnaire pour représenter le résultat de Zoé. Je représente aussi le résultat de Noah en dessinant $\frac{2}{5}$ du tout sur une autre bande fractionnaire. En regardant les 2 bandes fractionnaires, je réalise que Noah a réussi à glisser sur une plus longue distance que Zoé. En effet, $\frac{2}{5}$ ou 2 un cinquième est plus long que la bande de Zoé qui indique $\frac{2}{10}$ ou 2 un dixième.

Cependant, j’observe que si Zoé avait réussi l’exploit de glisser sur une autre distance de $\frac{2}{10}$, elle aurait réussi à glisser sur la même distance que Noah. Grâce à cette observation, je constate que $\frac{4}{10}$ ou 4 un dixième et $\frac{2}{5}$ sont des fractions équivalentes.

Source : En avant, les maths!, 3^e année, CM, Nombres, p. 3.

Activité 3 : les petites balles rebondissantes!

---

Le personnel enseignant a caché 8 petites balles rebondissantes un peu partout dans la cour d’école. Les 8 balles représentent un tout. Les élèves ont 5 minutes pour partir à la recherche des balles. Voici les questions posées aux élèves comme indices.

• Si $\frac{1}{2}$ des 8 balles sont vertes, combien de balles sont vertes?
• Si $\frac{2}{4}$ des 8 balles sont violettes, combien de balles sont violettes?
• Que peux-tu dire à propos $\frac{4}{8}$ des balles? Que remarques-tu?

Stratégie

Représentation de fractions équivalentes à l’aide d’un modèle d’un ensemble d’objets

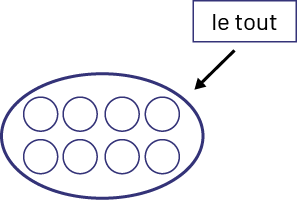
Pour trouver la réponse à la 1^re question, je prends 8 jetons pour représenter les 8 balles.

Je vois que le tout est composé de 8 balles.

Je dois maintenant partager les 8 balles en 2 groupes égaux pour que le résultat représente $\frac{1}{2}$.

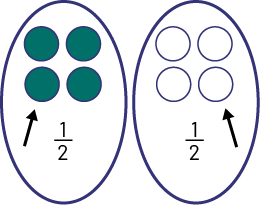
Je vois 4 balles. C’est le résultat de $\frac{1}{2}$ des 8 balles récoltées. Donc, 4 balles sont vertes.

Pour trouver la réponse à la 2^e question, je dois maintenant partager les 8 balles en 4 groupes égaux pour que le résultat représente des $\frac{1}{4}$. Je dois donc mettre 2 balles dans chaque groupe pour représenter $\frac{1}{4}$ des 8 balles récoltées. Je cherche à connaître le nombre de balles qui représente 2 fois $\frac{1}{4}$ ou $\frac{2}{4}$ des 8 balles récoltées, donc j’encercle 2 groupes de $\frac{1}{4}$ et cela fait un total de 4 balles.

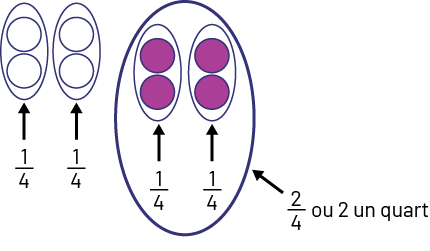Image Deux ovales sont représentés. Dans chaque ovale, il y a 4 balles, celles de l’ovale de gauche sont vertes. Une flèche pointe les balles, on peut lire la fraction un demi.

Je remarque qu’il y a 2 balles dans $\frac{1}{4}$ des balles récoltées.

Je remarque qu’il y a 4 balles dans $\frac{2}{4}$ des balles récoltées, comme dans la demie des 8 balles récoltées. Donc, je sais que 4 balles sont violettes.

Pour trouver la réponse à la troisième question, je dois maintenant partager les 8 balles en 8 groupes égaux pour que le résultat représente des $\frac{1}{8}$.

Je dois donc mettre 1 balle dans chaque groupe. Je cherche à connaître le nombre de balles qui représente 4 un huitième ou $\frac{4}{8}$ des balles récoltées. Donc, j’encercle 4 groupes de $\frac{1}{8}$ et cela fait un total de 4 balles. Il reste un autre groupe de 4 balles. Donc, cela fait un autre groupe de $\frac{4}{8}$.

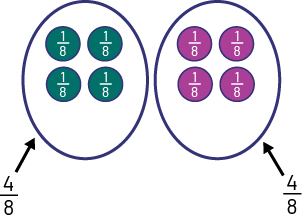Image Un ovale représente l’ensemble de 4 balles vertes. Chaque balle verte est annotée un huitième. L’ensemble représente la fraction 4 sur 8 ou 4 huitièmes. Un deuxième ovale représente l’ensemble de 4 balles violettes. Chaque balle est annotée un huitième. L’ensemble représente la fraction 4 sur 8 ou un huitième.

Donc, sur un tout de 8 balles, $\frac{4}{8}$ des balles peuvent être vertes ou $\frac{4}{8}$ des balles peuvent être violettes.

Je vais positionner côte à côte les regroupements.

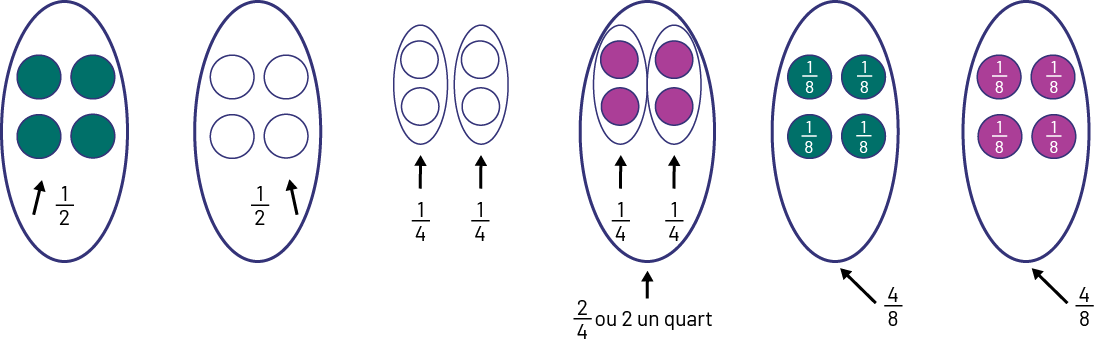
Image Deux ovales sont représentés. Dans chaque ovale, il y a 4 balles, celles de l’ovale de gauche sont vertes.Une flèche pointe les balles, on peut lire la fraction un demi.À côté on peut voir :8 balles sont placées sur 2 rangées de 4 balles chacune. Des ovales encerclent les balles 2 par 2, chaque ovale représente un quart des balles. Un grand ovale encercle 2 petits ovales, cela représente la fraction 2 sur 4 ou 2 un quart.Puis : Un ovale représente l’ensemble de 4 balles vertes. Chaque balle verte est annotée un huitième. L’ensemble représente la fraction 4 sur 8 ou 4 huitièmes.Un deuxième ovale représente l’ensemble de 4 balles violettes. Chaque balle est annotée un huitième. L’ensemble représente la fraction 4 sur 8 ou un huitième.

Je constate qu’il y a 4 balles dans $\frac{1}{2}$ des 8 balles.

Je constate qu’il y a 4 balles dans le $\frac{2}{4}$ ou 2 un quart des 8 balles.

Je constate qu’il y a 4 balles dans le $\frac{4}{8}$ des 8 balles.

Je compare le $\frac{1}{2}$ du tout, le $\frac{2}{4}$ du tout et le $\frac{4}{8}$ du tout et je remarque que j’ai 4 balles dans chaque cas. Donc, $\frac{1}{2}$, $\frac{2}{4}$ et $\frac{4}{8}$ sont des fractions équivalentes.

Source : En avant, les maths!, 3^e année, CM, Nombres, p. 4 à 6.