B1.7 Represent and solve fair-share problems that focus on determining and using equivalent fractions, including problems that involve halves, fourths, and eighths; thirds and sixths; and fifths and tenths.
Activity 1: Let's Compare Fractions (Representing and Comparing Fractions)
Directions
Ask 6 students to form 2 equal groups.
Ask the following question:
- What fraction does each group represent?
Write this fraction on 2 cards and ask a student from each group to show it.
- How many students are in each half?
Ask 6 other students to form 3 equal groups.
Ask the following question:
- What fraction does each group represent?
Write this fraction on 3 cards and have one student from each group show it.
- How many students are in each third?
Point out that there are more students in one half of the first group (3 students) than in one third of the second group (2 students).
Ask 6 students to form 2 equal groups.
Ask 9 students to form 3 equal groups.
Proceed in the same way as above.
Point out that there are the same number of students in one half of the group of 6 students and one third of the group of 9 students, namely, 3 students in each group.
Ask 6 students to form 2 equal groups.
Ask 12 other students to form 3 equal groups.
Proceed in the same way as above.
Point out that there are fewer students in the one half of the group of 6 students than in the one third of the group of 12 students.
Repeat by comparing \(\frac{1}{4}\) and \(\frac{1}{2}\) of 20 tokens.
Note: Point out that the unit fraction (\(\frac{1}{x}\) of a set) always represents 1 group of a set divided into x equal groups, but that the fraction of a set represents a different quantity of elements depending on the number of elements in the set.
Intervention
Continue the questioning used in direct instruction.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 56-57.
Activity 2: The County Fair
At the county fair, teachers organized games in the schoolyard. One of the stations featured a slide mat, where students would run, take off, and slide as far as possible on a wet plastic mat. To analyze the results, the teachers divided the length of the mats into either 5 or 10 equal sections.
Zoe slid, and the teacher claims she slid \(\frac{2}{10}\) of the mat. Noah slid, and the teacher claims he slid \(\frac{2}{5}\) of the mat. What do you notice? What must happen for the two students to slide an equal distance?
Strategy
Representation of Equivalent Fractions Using a Linear Model
Here are the results of Zoe and Noah.
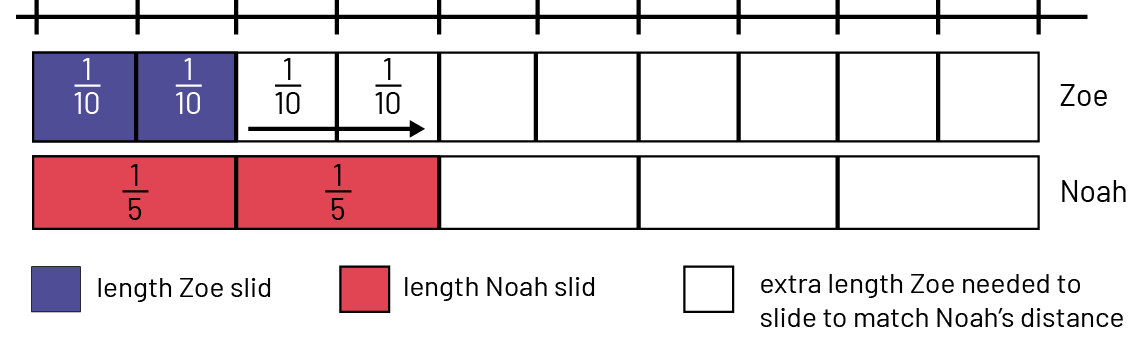
I draw \(\frac{2}{10}\) on a fractional strip to represent Zoe's result. I also represent Noah's result by drawing \(\frac{2}{5}\) on another fractional strip. Looking at the 2 fractional strips, I realize that Noah managed to slide a longer distance than Zoe. Indeed, \(\frac{2}{5}\) or 2 one fifths is longer than Zoe's strip which indicates \(\frac{2}{10}\) or 2 one tenths. However, I observe that if Zoe had managed to slide another distance of \(\frac{2}{10}\), she would have managed to slide the same distance as Noah. From this observation, I can see that \(\frac{4}{10}\) or 4 one tenths and \(\frac{2}{5}\) are equivalent fractions.
Source: translated from En avant les maths! 3e, CM, Nombres, p. 3.
Activity 3: The Little Bouncing Balls!
The teachers hid 8 small bouncing balls all over the schoolyard. The 8 balls represent a whole. Students have 5 minutes to search for the balls. Here are the clues given to the students as questions.
- If \(\frac{1}{2}\) of the 8 balls are green, how many balls are green?
- If \(\frac{2}{4}\) of the 8 balls are purple, how many balls are purple?
- What can you say about \(\frac{4}{8}\) of the balls? What do you notice?
Strategy
Representation of Equivalent Fractions Using the Set Model
To find the answer to the 1st question, I take 8 tokens to represent the 8 balls.
I see that the whole is composed of 8 balls.
I need to divide the 8 balls into two equal groups so that the result represents \(\frac{1}{2}\).
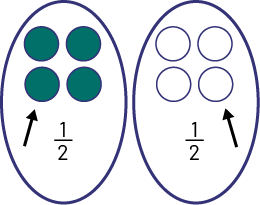
I see 4 balls. This is the result of \(\frac{1}{2}\) of the 8 balls collected. So 4 balls are green.
To find the answer to the 2nd question, I must now divide the 8 balls into 4 equal groups so that the result represents \(\frac{1}{4}\). So I have to put 2 balls in each group to represent \(\frac{1}{4}\) of the 8 balls. I want to know the number of balls that represents 2 times \(\frac{1}{4}\) or \(\frac{2}{4}\) of the 8 balls collected, so I circle 2 groups of \(\frac{1}{4}\) and that makes a total of 4 balls.
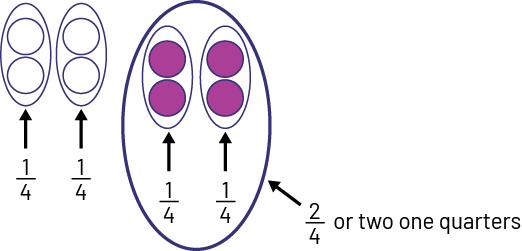
I notice that there are 2 balls in \(\frac{1}{4}\) of the collected balls.
I notice that there are 4 balls in \(\frac{2}{4}\) of the collected balls, as in the half of the 8 collected balls. So I know that 4 balls are purple.
To find the answer to the third question, I now need to divide the 8 balls into 8 equal groups so that the result represents \(\frac{1}{8}\).
So I have to put 1 ball in each group. I want to know the number of balls that represents 4 one eighths or \(\frac{4}{8}\) of the balls collected. I circle 4 groups of \(\frac{1}{8}\) and that makes a total of 4 balls. There remains another group of 4 balls. So that makes another group of \(\frac{4}{8}\).
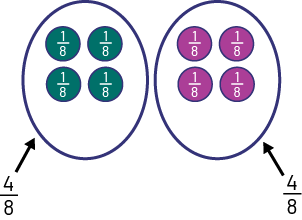
So out of a set of 8 balls, \(\frac{4}{8}\) balls can be green or \(\frac{4}{8}\) balls can be purple.
I will position the groups side by side.

I see that there are 4 balls in \(\frac{1}{2}\) of the 8 balls.
I see that there are 4 balls in the \(\frac{2}{4}\) or 2 fourths of the 8 balls.
I see that there are 4 balls in the \(\frac{4}{8}\) of the 8 balls.
I compare the \(\frac{1}{2}\) of the whole, the \(\frac{2}{4}\) of the whole and the \(\frac{4}{8}\) of the whole and I notice that I have 4 balls in each case. So \(\frac{1}{2}\), \(\frac{2}{4}\) and \(\frac{4}{8}\) are equivalent fractions.
Source: translated from En avant les maths! 3e, CM, Nombres, p. 5-6.
