B2.2 Se rappeler les faits de multiplication de 2, 5 et 10, et les faits de division associés, et démontrer sa compréhension de ces faits.
Habileté : se rappeler des faits de multiplication de 2, 5 et 10 et les faits de division associés
Pour apprendre les faits numériques de base relatifs à la multiplication et à la division, il ne suffit pas de les mémoriser. Il est important de comprendre que ces opérations peuvent être abordées de façons différentes.
La multiplication peut être représentée sous forme d’addition répétée, de dispositions rectangulaires ou d’un ensemble de groupes égaux. Voici quelques propriétés et stratégies qui favorisent la compréhension conceptuelle de la multiplication :
- la propriété de l’élément neutre dans la multiplication de nombres naturels (\(a \times 1\) donne toujours a);
- la propriété du 0 dans la multiplication de nombres naturels (\(0 \times a \) donne toujours 0);
- la propriété de commutativité \((2 \times 3 = 3 \times 2)\);
- la propriété de distributivité \([5 \times 6 = 5 \times (4 + 2) = (5 \times 4) + (5 \times 2)]\) ;
- la propriété d’associativité \([5 \times 12 = 5 \times (2 \times 6) = (5 \times 2) \times 6]\) ;
- l’opération inverse de la division.
La division peut être représentée sous forme de soustractions répétées, d’une répartition égale ou de partage. Voici quelques propriétés et stratégies qui favorisent la compréhension conceptuelle de la division :
- la propriété de l’élément neutre dans la division de nombres entiers (\( a \div 1\) donne toujours a);
- le rapport entre la division et le sens de la fraction (12 bonbons divisés en 3 groupes représentent à la fois \(12 \div 3\) et le tout divisé en 3 parties);
- l’opération inverse de la multiplication.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 21-22.
Régularités dans des suites de nombres
Les élèves développent une meilleure compréhension du sens des opérations arithmétiques en explorant les régularités qu’elles génèrent dans les suites de nombres. Les élèves peuvent utiliser la droite numérique ou la grille de nombres pour analyser les suites de nombres obtenues lorsqu’on compte par intervalles. Par exemple, si on compte par intervalles de 10 à partir d’un chiffre quelconque de 0 à 9, tous les nombres obtenus se termineront par ce chiffre (par exemple, si on commence à compter à 3, on aura la suite 3, 13, 23, 33, 43…). Les élèves peuvent utiliser du matériel de manipulation pour découvrir le lien qui existe entre les nombres pairs et la divisibilité par 2 (par exemple, en tentant de répartir également un nombre pair ou un nombre impair de cubes entre 2 élèves).
L’étude des régularités dans les suites de nombres facilite aussi l’apprentissage des faits numériques de base (par
exemple, tous les multiples de 5, soit 5, 10, 15, 20, 25…, se terminent par 5 ou 0) et l’établissement de liens entre
les nombres (par exemple, tous les multiples de 10  sont aussi multiples de 5
sont aussi multiples de 5 ).
).
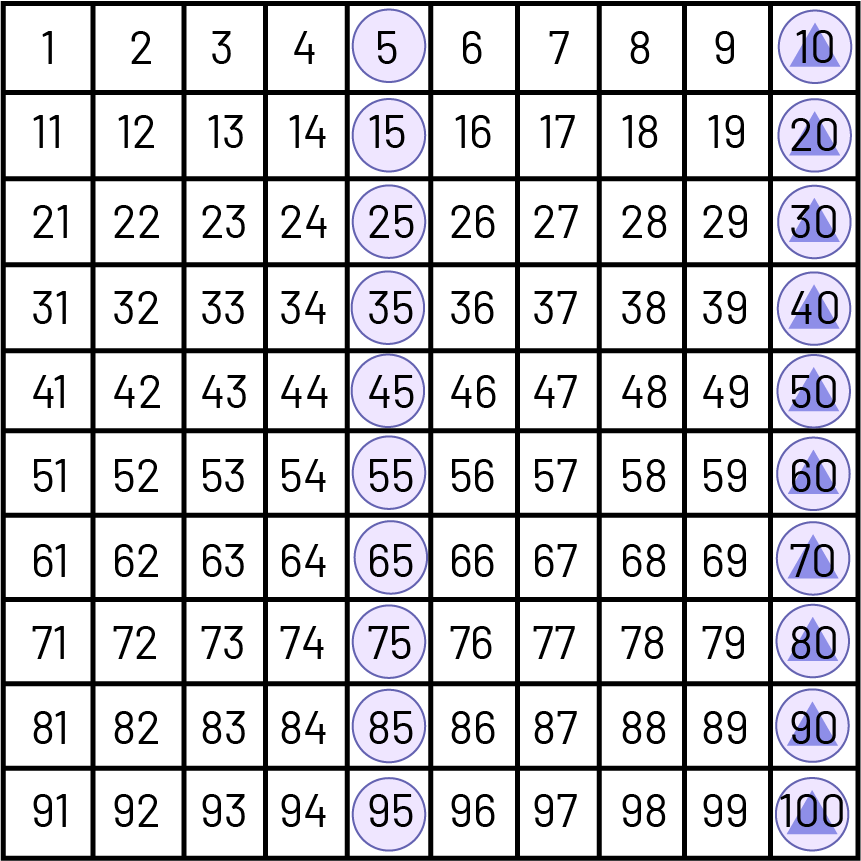 Image Grille de nombres de un à 100. Tous les multiples de 5 sont encerclés : 5, dix, 15, 20, 25,
30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95,
100. Tous les multiples de dix sont marqués d’un triangle : dix, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Image Grille de nombres de un à 100. Tous les multiples de 5 sont encerclés : 5, dix, 15, 20, 25,
30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95,
100. Tous les multiples de dix sont marqués d’un triangle : dix, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Les élèves prennent généralement plaisir à découvrir des régularités dans les suites de nombres générées par les opérations arithmétiques, chaque découverte suscitant habituellement un sentiment d’émerveillement. Les activités liées à la recherche de régularités encouragent les élèves à jongler avec les nombres et favorisent le développement de la pensée divergente et de l’esprit d’analyse, 2 composantes importantes de la pensée mathématique. De plus, l’habileté à explorer les régularités est essentielle à l’étude de l’algèbre et de la géométrie.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 30-31.
Représentation des faits numériques de base relatifs à la multiplication et à la division
Utiliser des modèles pour représenter les faits numériques de base peut aider les élèves à comprendre le sens des opérations fondamentales et à en amoindrir le caractère abstrait. De nombreux modèles peuvent être élaborés à l’aide du matériel ci-dessous pour amener les élèves à comprendre la multiplication et la division :
- des objets mobiles, comme des jetons, des bâtonnets et des carreaux, ainsi que divers contenants pour les y placer;
- des cubes emboîtables;
- du matériel visuel, comme des illustrations;
- des dispositions rectangulaires (arrangement de rangées et de colonnes);
- du matériel de base 10;
- des pièces de monnaie (1 ¢, 5 ¢, 10 ¢, 25 ¢ et 1 $);
- du papier quadrillé;
- des droites numériques;
- des grilles de nombres.
Les modèles de tous genres peuvent aider les élèves à établir des relations et ainsi à mieux comprendre ce que représentent les symboles dans les opérations. Les élèves ont besoin de travailler avec des représentations qui les aident à percevoir les relations entre la multiplication et les additions répétées, et entre la multiplication et la division (les élèves qui font l’apprentissage de la division longue peuvent également tirer parti des représentations qui les aident à percevoir les divisions longues comme des soustractions répétées ou des additions répétées). La compréhension des dispositions rectangulaires comme outil de multiplication ou de division se développe avec le temps et la pratique. Une fois que les élèves peuvent se représenter des faits tels que \(5 \times 6\) à l’aide de dispositions rectangulaires, ils peuvent se servir de celles-ci pour trouver la réponse à \(50 \times 6\), et ainsi de suite.
Les représentations de tous genres aident les élèves à faire des rapprochements entre les modèles, les symboles et les mots. On trouvera ci-dessous différentes représentations du fait numérique de base \(2 \times 6\). Chacune des 5 représentations est appropriée.
Rappelons seulement que les élèves éprouvent moins le besoin de recourir aux représentations visuelles à mesure que certains automatismes se développent pour résoudre les faits numériques de base. Au cycle primaire, quelques élèves seulement développeront certains automatismes dans l’application des faits numériques de base relatifs à la multiplication. L’essentiel à ce stade est de mettre l’accent sur la compréhension du concept et sur les stratégies se rattachant à la multiplication.
 Image Exemple d’illustration : Deux rectangles, dans lesquels, il y a 2 rangées de 3 cœurs.
Exemple de droite numérique : Droite numérique de, un à 15, par intervalles de, un. Des flèches représentent des bonds
de 6 au départ du, un. Exemple de matériel de base dix : 12 blocs unités sont rangés en 4 colonnes de 4, puis
représenté par un bloc de dizaine et 2 blocs d’unité. Exemple de dispositions rectangulaire : 2 rangées de 6 jetons. 2
rangées multipliées par 6 colonnes. Exemple avec un géoplan : Sur le géoplan en haut à gauche 6 carrés sont créés, à
la verticale, puis un espace, et enfin, 6 autres carrés à la
verticale. Exemple de problème écrit : Deux boîtes de six biscuits font douze biscuits en tout. Exemple de symboles :
2 multiplié par 6 égale 12.
Image Exemple d’illustration : Deux rectangles, dans lesquels, il y a 2 rangées de 3 cœurs.
Exemple de droite numérique : Droite numérique de, un à 15, par intervalles de, un. Des flèches représentent des bonds
de 6 au départ du, un. Exemple de matériel de base dix : 12 blocs unités sont rangés en 4 colonnes de 4, puis
représenté par un bloc de dizaine et 2 blocs d’unité. Exemple de dispositions rectangulaire : 2 rangées de 6 jetons. 2
rangées multipliées par 6 colonnes. Exemple avec un géoplan : Sur le géoplan en haut à gauche 6 carrés sont créés, à
la verticale, puis un espace, et enfin, 6 autres carrés à la
verticale. Exemple de problème écrit : Deux boîtes de six biscuits font douze biscuits en tout. Exemple de symboles :
2 multiplié par 6 égale 12.
Stratégies pour apprendre les faits numériques de base relatifs à la multiplication et à la division
Le personnel enseignant peut aider les élèves à élaborer des stratégies efficaces pour dégager les faits en faisant appel à leur raisonnement et en les encourageant à chercher des régularités et des relations entre les nombres. Les stratégies décrites ci-dessous permettent aux élèves de s’appuyer sur des connaissances déjà acquises pour déterminer des faits inconnus. Par exemple, savoir que \(2 \times 2 = 4\) aide l’élève à trouver que \(2 \times 3 = 6\) (puisque dans \(2 \times 3\), il y a 2 de plus que dans \(2 \times 2\)), ce qui dénote une importante aptitude de raisonnement. Les stratégies devraient être enseignées dans un contexte de résolution de problèmes. À cet égard, il faut :
- choisir des problèmes se prêtant bien à l’utilisation des stratégies enseignées;
- donner aux élèves des occasions de modeler eux-mêmes la stratégie à l’étude;
- faire en sorte que les élèves appliquent la stratégie dans un contexte signifiant.
Les stratégies qui suivent ne sont pas présentées selon un ordre particulier. Il arrive que des élèves trouvent certaines stratégies plus utiles que d’autres ou ignorent certaines stratégies au profit de leurs propres stratégies. D’autres trouvent plus facile de mémoriser les faits que de s’appuyer sur une stratégie. Quel que soit le cas, l’objectif premier du personnel enseignant est d’amener tous les élèves à bien comprendre la multiplication et la division.
La commutativité
Les élèves bénéficient d’expériences qui les aident à reconnaître la propriété de commutativité de la multiplication (\(2 \times 4 = 4 \times 2\)). Les élèves qui comprennent la commutativité peuvent mettre à profit la moitié des faits numériques de base pour apprendre l’autre moitié.
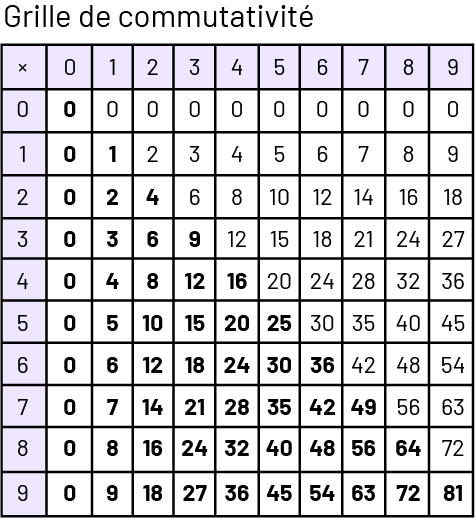 Image
Grille de commutativité. Dans la case du coin en haut à gauche, il y a le symbole multiplié. Les autres cases de la
première rangée et de la première colonne vont de zéro à 9. Les autres cases contiennent le résultat des
multiplications entre les nombres des premières cases.
Image
Grille de commutativité. Dans la case du coin en haut à gauche, il y a le symbole multiplié. Les autres cases de la
première rangée et de la première colonne vont de zéro à 9. Les autres cases contiennent le résultat des
multiplications entre les nombres des premières cases.
Les doubles
La table de multiplication de 2 devrait être reliée aux connaissances que les élèves ont déjà acquises sur l’addition de doubles. Cette stratégie est particulièrement importante parce que les élèves qui maîtrisent bien la table de 2 peuvent relier ces faits numériques à la table de multiplication de 3. En effet, si \(2 \times 4\) donne 8, il s’ensuit que \(3 \times 4\) est égal à 8 plus un autre 4.
Les faits numériques relatifs à 5
Les élèves qui sont habitués à compter par 5 et à reconnaître les régularités de 5 dans une grille de nombres n’ont généralement pas de difficulté à apprendre les faits numériques de base relatifs à 5. Il existe toute une gamme de chansons, de comptines et de livres d’histoire portant sur le 5 dont on peut se servir pour appuyer l’apprentissage de cette stratégie.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 23-27.
Multiplier par 10
Les élèves doivent apprendre à maîtriser l’effet de la multiplication et de la division par 10 et des multiples de 10. L’explication de ces opérations se résume souvent à l’énoncé suivant : « Lorsqu’on multiplie par 10, on ajoute un 0 et lorsqu’on divise par 10, on enlève un 0 ». Cet énoncé est à déconseiller, car il ne tient pas compte de la compréhension des opérations et les élèves sont alors encouragés à appliquer un « truc » de façon mécanique, sans pouvoir faire de lien au cours d’une multiplication ou d’une division par des nombres tels que 10, 100 ou 1 000.
Il est utile pour les élèves de reconnaître que des opérations comme \(5 \times 10\) ou \(60 \div 2 \) peuvent être considérées comme \(5 \times 1\) dizaine, 6 dizaines \(\div 2\). On peut alors mieux comprendre l’apparition ou la disparition des chiffres « 0 » dans les opérations.
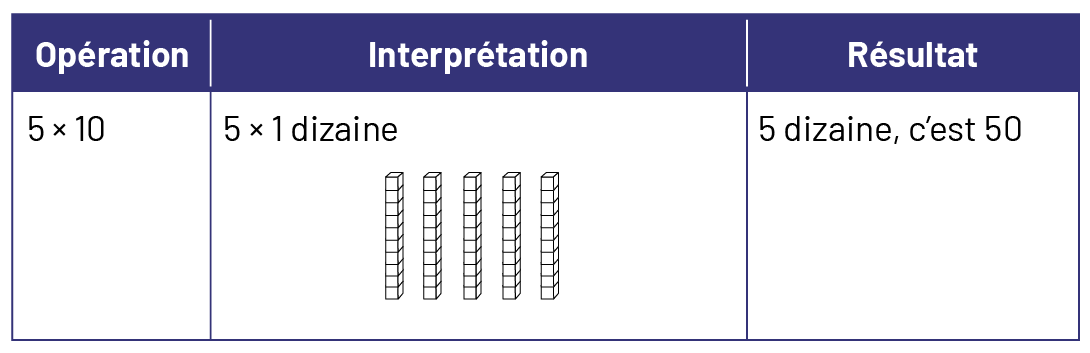
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 91.
La relation inverse de la division et de la multiplication
Les élèves qui maîtrisent les faits numériques de base relatifs à la multiplication devraient se servir de ces acquis pour découvrir les faits numériques de base relatifs à la division. Il est recommandé d’enseigner simultanément la division et la multiplication afin de mettre en évidence les relations entre les 2. Lorsque les élèves unissent 4 groupes de 5 éléments pour un total de 20, le personnel enseignant devrait les encourager à se rendre compte que lorsque ce total est à nouveau réparti entre 4 groupes, chaque groupe compte 5 éléments.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 29.
