GEEM - Skills and Knowledge

B2.2 Recall and demonstrate multiplication facts of 2, 5, and 10, and related division facts.

Skill: Recalling Multiplication Facts of 2, 5 and 10 and Related Division Facts

To learn the basic multiplication and division facts, it is not enough to memorize them. It is important to understand that these facts can be approached in different ways.

For example, multiplication can be represented as repeated addition, area (arrays), or sets of equal groups. Properties and strategies that support conceptual understanding of multiplication include:

the identity property of multiplication: ($a\; \times \;1$ always equals a);
the zero property of multiplication: ($0 \times \; n$ = 0);
the commutative property $\left( {2\; \times \;3\; = \;3 \times \;2} \right)$;
the distributive property $\left[ {5\; \times \;6\; = \;5\; \times \;\left( {4\; + \;2} \right)\; = \;\left( {5\; \times \;4} \right)\; + \;\left( {5\; \times \;2} \right)} \right]$;
the associative property $\left[ {5\; \times \;12\; = \;5\; \times \;\left( {2\; \times \;6} \right)\; = \;\left( {5\; \times \;2} \right)\; \times \;6} \right]$;
the inverse operation of the division.

Division can be represented as repeated subtraction, equal grouping (quotative division) or equal-sharing (partitive division). Properties and strategies that support conceptual understanding of division include:

the identity property, which states that when dividing an amount by 1, the amount stays the same ($a\; \div \;1$ always equals a);
the relationship between division and fractions (12 candies divided into 3 groups represent both $12\; \div \;3$ and the whole divided into 3 equal parts);
the inverse operation of the multiplication.

Source: translated from Guide d'enseignement efficace des mathématiques de la maternelle à la 6^e année, Fascicule 5, p. 21-22.

Patterns in Numbers

Students develop a better understanding of the meaning of mathematical operations by exploring the patterns they generate in number sequences. They can use a number line or a hundreds chart to analyze number sequences obtained when counting by intervals. For example, if we count by intervals of 10 from any number from 0 to 9, all the numbers obtained will end with this number (for example, if we start counting at 3, we will have the sequence 3, 13 , 23, 33, 43…). Students can use manipulatives to discover the connection between even numbers and divisibility by 2 (for example, by trying to divide an even number or an odd number of cubes equally between 2 students).

The study of patterns in number sequences also facilitates the learning of basic number facts (for example, all multiples of 5, that is 5, 10, 15, 20, 25, end in 5 or 0) and the building of connections between numbers (for example, all multiples of 10[▲] are also multiples of 5[●] ).

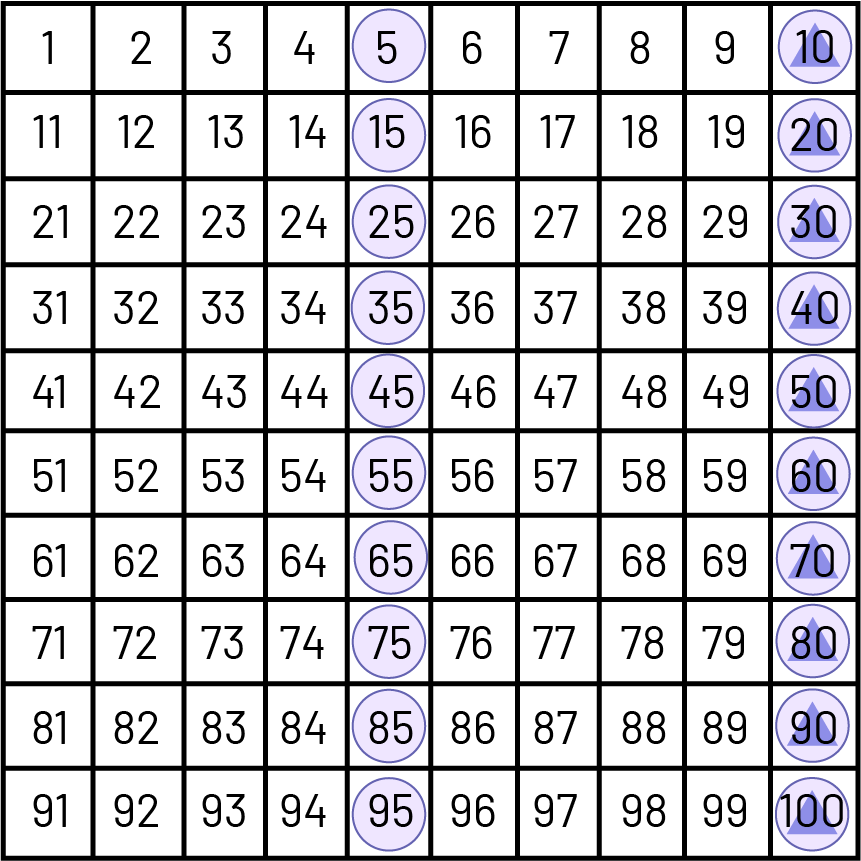
Students generally enjoy identifying patterns in the number sequences generated by mathematical operations, with each discovery usually evoking a sense of wonder. Activities related to finding patterns encourage students to juggle numbers and promote the development of divergent thinking and analytical skills, two important components of mathematical thinking. In addition, the ability to explore patterns is essential to the study of algebra and geometry.

Source: translated from Guide d’enseignement efficace des mathématiques de la 1^re à la 3^e année, Numération et sens du nombre, p. 30-31.

Representation of Multiplication and Division Facts

Using models to represent basic number facts can help students understand the meaning of basic operations and lessen their abstract nature. Many models can be developed using the materials below to build students' understanding of addition and subtraction:

concrete objects, such as counters, sticks, tiles, and various containers to place them in;
interlocking cubes;
visual material, such as illustrations;
arrays;
base ten blocks;
coins (1¢, 5¢, 10¢, 25¢, $1and $2);
grid paper;
number lines;
hundred charts.

Models of all kinds can help students make connections and thus better understand what symbols represent in operations. Students need to work with representations that help them perceive relationships between multiplication and repeated addition, and between multiplication and division (students learning long division can also benefit from representations that help them to perceive long divisions as repeated subtraction or repeated addition). Understanding that arrays are a model for multiplication or division develops with time and practice. Once students can represent facts such as $5\; \times \;6$ using arrays, they can use these to find the answer to $50 \; \times \;6$, and so on.

Representations of all kinds help students make connections between models, symbols and words. Below are different representations of the basic number fact $2\; \times \;6$ . Each of the 5 representations is appropriate.

Students feel less need to use visual representations as they develop automaticity with basic number facts. In the primary grades, only a few students will develop some automaticity in the application of basic number facts related to multiplication. The key at this stage is to focus on conceptual understanding and strategies related to multiplication.

Strategies for Learning Multiplication and Division Facts

Teachers can help students develop effective strategies for finding facts by using their reasoning and encouraging them to look for patterns and relationships between numbers. The strategies described below allow students to use prior knowledge to determine unknown facts. For example, knowing that $2 \times 2 = 4$ helps the student find that $2 \times 3 = 6$ (since $2 \times 3$, there are 2 more than in $2 \times 2$), which indicates strong reasoning skills. Strategies should be taught in a problem-solving context. In this regard, one should:

select problems that lend themselves well to the use of the strategies taught;
provide opportunities for students to model the strategy under consideration;
have students apply the strategy in a meaningful context.

The following strategies are not presented in any particular order. Some students may find some strategies more useful than others, or may ignore some strategies in favour of their own. Others find it easier to memorize facts than to rely on a strategy. Whatever the case, the teacher's primary goal is to get all students to fully understand multiplication and division.

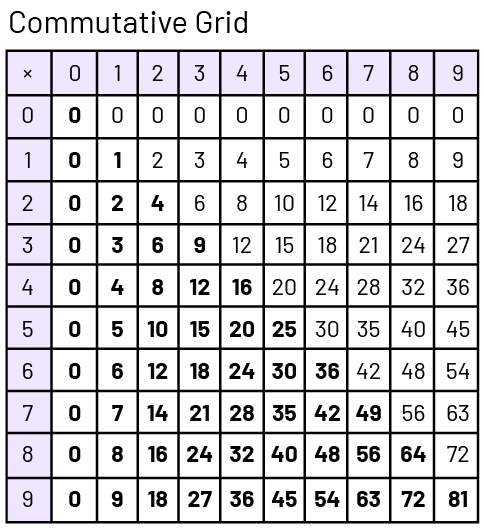
Commutative Property

Students benefit from experiences that help them recognize the commutative property of multiplication ($2 \times 4 = 4 \times 2$). Students who understand commutative property can use half of the basic number facts to learn the other half.

Doubles

The multiplication facts of 2 should be related to the knowledge students have already learned about adding doubles. This strategy is particularly important because students who are familiar with the multiplication facts of 2 can relate these number facts to the 3 times table. Indeed, if $2 \times 4$ is 8, it follows that $3 \times 4$ equals 8 plus another 4.

Five Facts

Students who are accustomed to counting by 5s and recognizing patterns of 5s in a number chart generally have no difficulty learning the five facts. There are a variety of songs, rhymes, and storybooks based on fives that can be used to support learning this strategy.

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6^e année, Fascicule 5, p. 23-27.

Ten Facts

Students need to learn to master the effect of multiplication and division by 10 and multiples of 10. The explanation of these operations often boils down to the statement, "When you multiply by 10, you add a 0 and when you divide by 10, you take away a 0." This statement is not recommended because it does not take into account the understanding of operations and students are encouraged to apply a mechanical shortcut without being able to make a connection during multiplication or division by numbers such as 10, 100, or 1000.

It is helpful for students to recognize that operations like $5 \times 10$ or $60 \div 2 $ can be thought of as $5 \times 1$ tens, 6 tens $\div 2 $. We can then better understand the appearance or disappearance of the digit 0 when performing the operations.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 91.

Inverse Relationship of Division and Multiplication

Students who have mastered multiplication number facts should use this knowledge to uncover division number facts. It is recommended that division and multiplication be taught simultaneously to highlight the relationships between the two. When students create 4 groups of 5 items for a total of 20 items, teachers should encourage them to realize that when that total is again divided among 4 groups, each group has 5 items.

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6^e année, Fascicule 5, p. 29.