B2.3 Utiliser des stratégies de calcul mental, y compris l’estimation, pour additionner des nombres dont la somme est égale ou inférieure à 1 000 et pour soustraire des nombres naturels égaux ou inférieurs à 1 000, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental
La plupart des calculs effectués au quotidien sont reliés à un calcul mental. Les personnes qui acquièrent de bonnes habiletés de calcul mental ne dépendent pas de l’électronique ou du papier pour effectuer les calculs de la vie courante. Or, il est important de démystifier le calcul mental. Il ne s’agit pas d’utiliser un algorithme dans sa tête, mais de calculer avec souplesse et efficacité.
On peut faire appel à diverses activités pédagogiques qui permettent de développer le calcul mental. Peu importe la situation d’apprentissage, le personnel enseignant profite des occasions, lors d’échanges mathématiques, pour faire ressortir les relations qui existent entre les différentes stratégies de calcul mental utilisées par les élèves. Cela fait ressortir les ressemblances et les différences entre les stratégies ainsi que leurs forces et leurs faiblesses et aide les élèves à établir des liens et à assimiler d’autres stratégies.
Plusieurs stratégies de calcul mental sont basées sur la relation entre le tout et ses parties (décomposition et regroupement), sur l’établissement de relations entre les nombres et sur les propriétés des opérations. Souvent, ces stratégies proviennent d’un transfert de modèles utilisés au cours de l’apprentissage des opérations.
Exemples de stratégies de calcul mental
Appliquer une propriété des opérations
Utiliser la commutativité de l’addition.
\(68 + 27 + 12 = \mathord{?}\)
\(68 + 27 + 12 = 68 + 12 + 27\)
\(68 + 12 = 80\)
\(80 + 27 = 107\)
\(68 + 27 + 12 = 107\)
Utiliser les valeurs de position
Additionner 10, 20, 30, 100… à partir de n’importe quel nombre.
\(163 + 230 = \mathord{?}\)
\(163 + 200 = 363\)
363, 373, 383, 393
\(163 + 230 = 393\)
Décomposer les nombres
Décomposer un nombre ou des nombres.
\(78 + 29 = \mathord{?}\)
\(75 + 3 + 25 + 4 = 100 + 7\)
\(78 + 29 = 107\)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 111-112.
Pour faciliter la lecture et la compréhension de cette section, les opérations sont présentées sous forme d’expressions numériques et de modèles. En classe, en modelant les stratégies des élèves, le personnel enseignant devrait aussi représenter les opérations horizontalement, par exemple :
\(35 + 26\)
\(273 - 185\)
Addition
L’utilisation de matériel de manipulation est une des premières stratégies auxquelles les élèves ont recours. Ils peuvent prendre des objets de la classe tels que des billes, des jetons ou des blocs pour représenter, par exemple, \(86 + 56\), et employer des stratégies de dénombrement pour trouver la somme. Ces stratégies ne sont cependant pas très efficaces avec de grands nombres.
Une addition de grands nombres peut être représentée sur une droite numérique. Par exemple, les élèves pourraient effectuer \(435 + 223\) en décomposant \(223 \ (200 + 15 + 8)\) et en représentant l’opération comme suit :
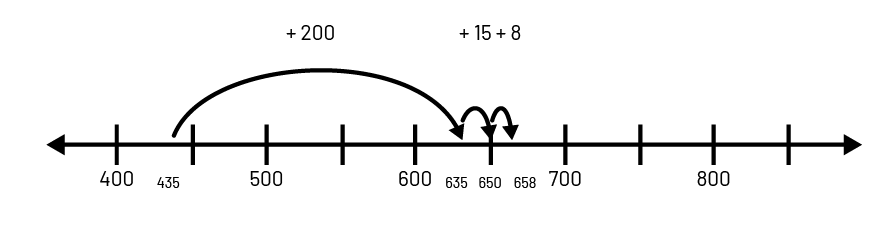 Image Droite numérique de 400 à 800 par intervalles de 50. Une flèche représente un bond qui
commence à 435 et qui finit à 635, donc un bond de plus 200. Une deuxième flèche fait un bond de 635 à 650, un bond de
plus 15. Une troisième flèche fait un bond de 650 à 658, un
bond de plus 8.
Image Droite numérique de 400 à 800 par intervalles de 50. Une flèche représente un bond qui
commence à 435 et qui finit à 635, donc un bond de plus 200. Une deuxième flèche fait un bond de 635 à 650, un bond de
plus 15. Une troisième flèche fait un bond de 650 à 658, un
bond de plus 8.
Au fil du temps, les élèves développent progressivement leur sens de l’abstraction et peuvent utiliser la même stratégie sans avoir recours à une droite numérique, mais en effectuant le calcul mentalement.
Le matériel de base 10 aide certains élèves à visualiser l’opération plus clairement.
Voici comment le matériel de base 10 peut servir pour représenter les additions.
Exemple
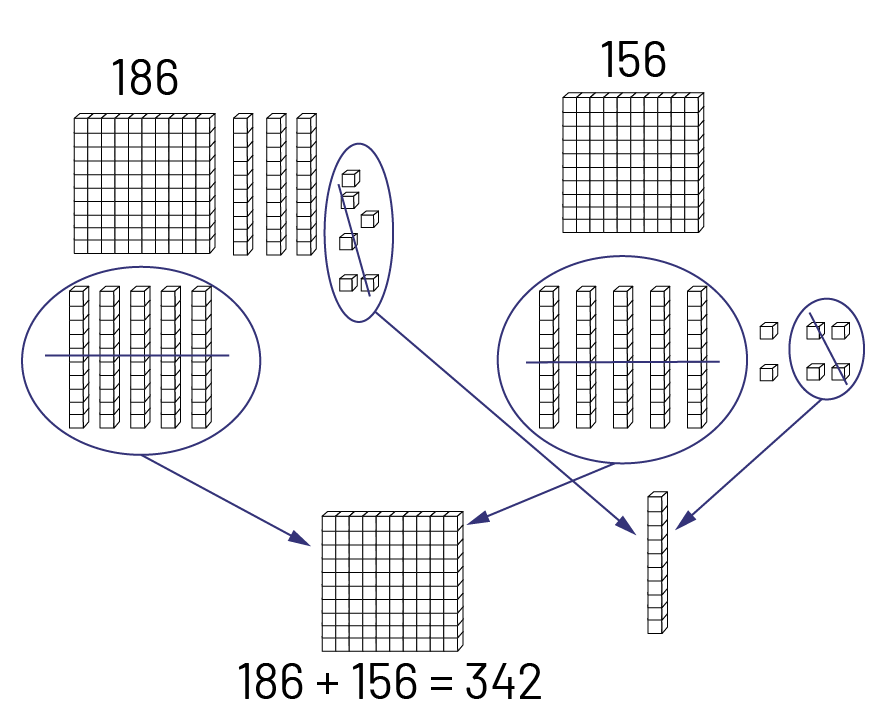 Image L’addition, 186 plus 156 égal 342, est représentée avec des blocs. 186 : un bloc de
centaine, 8 blocs de dizaines et 6 unités. 156 : un bloc de centaine, 5 blocs de dizaines et 6 unités. 5 blocs de
dizaines de 186 et de 156 donc mis ensemble et cela devient un bloc de centaine. 6 blocs d’unité de 186 et 4 blocs
d’unité de 156 sont mis ensemble, cela fait un bloc de dizaine.
Image L’addition, 186 plus 156 égal 342, est représentée avec des blocs. 186 : un bloc de
centaine, 8 blocs de dizaines et 6 unités. 156 : un bloc de centaine, 5 blocs de dizaines et 6 unités. 5 blocs de
dizaines de 186 et de 156 donc mis ensemble et cela devient un bloc de centaine. 6 blocs d’unité de 186 et 4 blocs
d’unité de 156 sont mis ensemble, cela fait un bloc de dizaine.
Les élèves peuvent aussi avoir recours à un tapis de valeur de position qui permet d’organiser le matériel selon la position du chiffre dans le nombre.
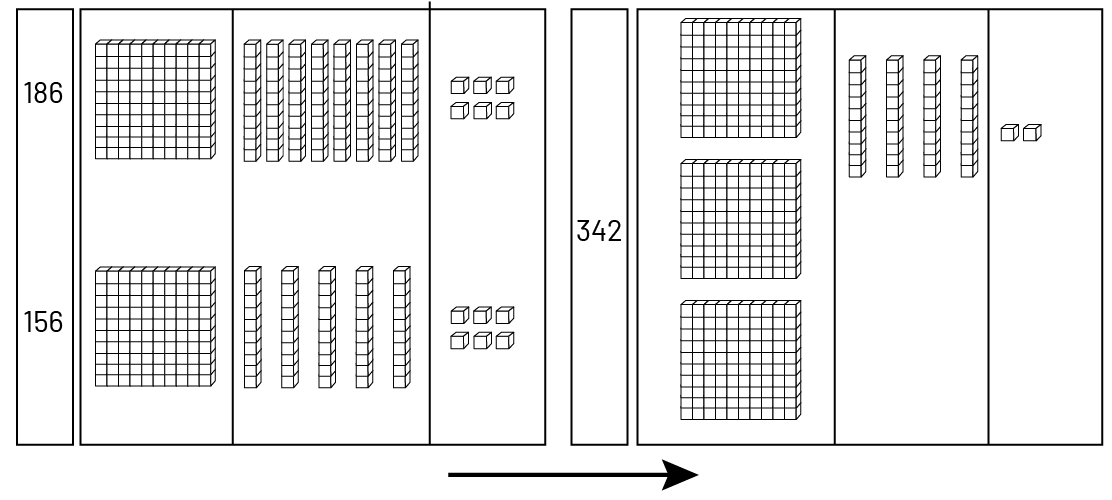 Image Des blocs sont utilisés sur un tapis de valeurs. Dans la première colonne, on retrouve les
nombres. Dans la deuxième colonne les blocs de centaines correspondant au nombre. Dans la troisième colonne, les blocs
des dizaines correspondant au nombre. Dans la quatrième colonne, les blocs d’unité correspondant au nombre. 186 : un
bloc de centaine, 8 blocs de dizaines et 6 blocs d’unités. 156 : un bloc de centaine, 5 blocs de dizaine, 6 blocs
d’unité. 342 : 3 blocs de centaines, 4 blocs de dizaines, 2 blocs d’unité.
Image Des blocs sont utilisés sur un tapis de valeurs. Dans la première colonne, on retrouve les
nombres. Dans la deuxième colonne les blocs de centaines correspondant au nombre. Dans la troisième colonne, les blocs
des dizaines correspondant au nombre. Dans la quatrième colonne, les blocs d’unité correspondant au nombre. 186 : un
bloc de centaine, 8 blocs de dizaines et 6 blocs d’unités. 156 : un bloc de centaine, 5 blocs de dizaine, 6 blocs
d’unité. 342 : 3 blocs de centaines, 4 blocs de dizaines, 2 blocs d’unité.
La même expression numérique (\(186 + 156\)) peut être représentée à l’aide d’illustrations. Ainsi, les élèves démontrent un certain niveau d’abstraction puisqu’un dessin quelconque représente 100, 10 ou 1.
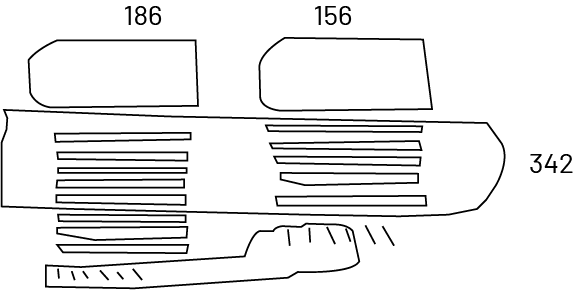 Image Une illustration qui représente les nombres 186 et 156, pour un total de 342 éléments. 186 :
un bloc qui représente la centaine, 8 bâtons représentent les dizaines et 6 bâtonnets représentent les unités.
156 : un bloc représente la centaine, 5 bâtons représentent les dizaines et 6 bâtonnets représentent les
unités.
Image Une illustration qui représente les nombres 186 et 156, pour un total de 342 éléments. 186 :
un bloc qui représente la centaine, 8 bâtons représentent les dizaines et 6 bâtonnets représentent les unités.
156 : un bloc représente la centaine, 5 bâtons représentent les dizaines et 6 bâtonnets représentent les
unités.
À partir de leurs expériences avec les nombres et quelques algorithmes, les élèves peuvent additionner en utilisant des algorithmes personnels. Selon l’enseignement qu’ils ont reçu, certains élèves ont recours au papier-crayon pour garder des traces de ce qu’ils font. Voici quelques exemples de stratégies de calcul.
Exemples
\(378 + 123\)
Stratégie de calcul mental
Algorithme personnel écrit
- Additionner de gauche à droite :
300 et 100 égalent 400.
70 et 20 égalent 90.
8 et 3 égalent 11.
Donc, 378 plus 123 égalent 501.
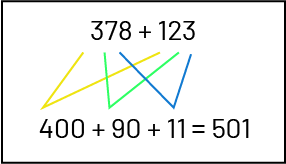 Image Dans un encadré, on explique l’addition : 378 plus 123 Des tracés jaunes partent de
centaines 300 et 100 et arrête au chiffre 400. Des tracés verts partent de dizaines 70 et 20, et arrête au chiffre
90. Des tracés bleus partent des unités, 8 et 3, et arrête au chiffre 11. On obtient ainsi la nouvelle addition :
400 plus 90 plus 11 égal 501.
Image Dans un encadré, on explique l’addition : 378 plus 123 Des tracés jaunes partent de
centaines 300 et 100 et arrête au chiffre 400. Des tracés verts partent de dizaines 70 et 20, et arrête au chiffre
90. Des tracés bleus partent des unités, 8 et 3, et arrête au chiffre 11. On obtient ainsi la nouvelle addition :
400 plus 90 plus 11 égal 501.
- Transformer le problème et compenser :
378, c’est 3 de plus que 375.
123, c’est 2 de moins que 125.
375 plus 125 égalent 500.
500 plus 3 moins 2, c’est égal à 501.
Donc, 378 plus 123, égalent 501.
\(378 + 123 = \mathord{?}\)
\(375 + 125 = 500\)
\(500 + 3 - 2 = 501\)
\(378 + 123 = 501\)
- Compter par intervalles selon la valeur de position :
378 plus 1 centaine donnent 478.
478 plus 2 dizaines donnent 488, 498.
498 plus 3 unités donnent 499, 500, 501.
Donc, 378 plus 123 donnent 501.
\(378 + 100 = 478\)
\(478 + 10 = 488\)
\(488 + 10 = 498\)
\(498 + 1 = 499\)
\(499 + 1 = 500\)
\(500 + 1 = 501\)
- Décomposer un des nombres selon la valeur de position :
378 plus 100 égalent 478.
478 plus 20 égalent 498.
498 plus 3 égalent 501.
Donc, 378 plus 123 égalent 501.
\(378 + 100 = 478\)
\(478 + 20 = 498\)
\(498 + 3 = 501\)
- Arrondir un nombre et compenser :
En arrondissant 378 à 380, je devrai compenser en enlevant
2 unités à 123; j’ai maintenant 380 plus 121, ce qui donne 501.
\(378 + 2 = 380\)
\(123 - 2 = 121\)
\(380 + 121 = 501\)
Soustraction
Comme pour l’addition, les élèves utilisent souvent du matériel de manipulation pour effectuer des soustractions. Cette stratégie les aide à saisir le concept de retrait, même si elle n’est pas très efficace lorsqu’il s’agit de grands nombres.
Le matériel de base 10 permet aux élèves d’effectuer la soustraction au moyen d’un retrait.
Exemple
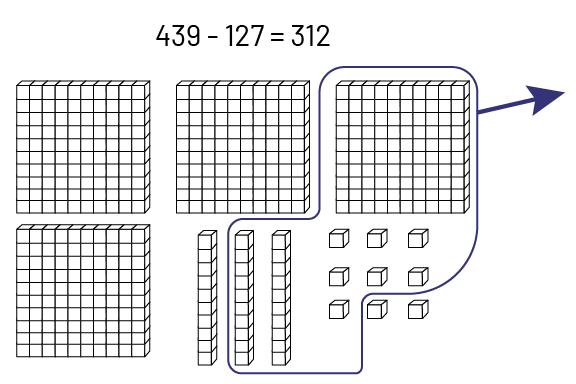
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 121-128.
Après avoir fait l’expérience de diverses façons de représenter les opérations, les élèves comprennent mieux leur valeur respective. Voici quelques exemples de stratégies de calcul.
Exemples
\(588 - 234\)
Stratégie de calcul mental
Algorithme personnel écrit
- Décomposer des nombres selon les valeurs de position et effectuer des soustractions partielles :
500 moins 200 égalent 300.
80 moins 30 égalent 50.
8 moins 4 égalent 4.
Donc, 588 moins 234 donnent 354.
\(588 - 234 = \mathord{?}\)
\(500 - 200 = 300\)
\(80 - 30 = 50\)
\(8 - 4 = 4\)
\(300 + 50 + 4 = 354\)
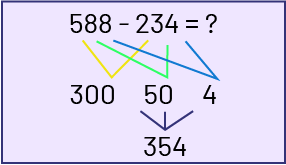 Image L’encadré explique la soustraction : 588 moins 234 égal inconnue. Des tracés jaunes
partent des centaines, 500 et 200, et s’arrêtent au nombre 300. Des tracés verts partent de dizaines, 80 et 30,
et s’arrêtent nombre 50. Des tracés bleus partent de unités 8 et 4, et arrêtent au nombre 4. 300, 50 et 4 sont
additionnés, on obtient 354.
Image L’encadré explique la soustraction : 588 moins 234 égal inconnue. Des tracés jaunes
partent des centaines, 500 et 200, et s’arrêtent au nombre 300. Des tracés verts partent de dizaines, 80 et 30,
et s’arrêtent nombre 50. Des tracés bleus partent de unités 8 et 4, et arrêtent au nombre 4. 300, 50 et 4 sont
additionnés, on obtient 354.
- Arrondir les nombres, soustraire et rajuster :
J’arrondis 588 à 600. Je soustrais 200
(400), ensuite 30 (370), puis 4 (366).
J’enlève 12 (ajouté à 588 au début).
J’obtiens donc 354.
\(588 - 234\)
\(600 - 234\)
\(600 - 200 = 400\)
\(400 - 30 = 370\)
\(370 - 4 = 366\)
\(366 - 12 = 354\)
- Soustraire par la gauche :
588 moins 200 égalent 388.
388 moins 30 égalent à 358.
358 moins 4 égalent 354.
\(588 - 234 = \mathord{?}\)
\(588 - 200 = 388\)
\(388 - 30 = 358\)
\(358 - 4 = 354\)
\(588 - 234 = 354\)
- Décomposer les nombres :
Je sais que 500 moins 200 donnent 300, que 88, c’est 84
plus 4 et que 84 moins 34 donnent 50. Il ne me reste plus qu’à
additionner 300, 4 et 50, ce qui donne 354.
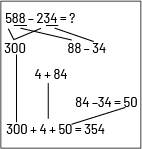 Image Explications de la soustraction : 588 moins 234 égal inconnue. Les centaines sont mises
en évidence par un trait, 500 moins 200 égal 300. Les dizaines et les unités sont mises en évidence par un trait :
88 moins 34. 4 plus 84. 84 moins 34 égal 50. 300 plus 4plus 50 égal 354.
Image Explications de la soustraction : 588 moins 234 égal inconnue. Les centaines sont mises
en évidence par un trait, 500 moins 200 égal 300. Les dizaines et les unités sont mises en évidence par un trait :
88 moins 34. 4 plus 84. 84 moins 34 égal 50. 300 plus 4plus 50 égal 354.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 130-131.
Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec la soustraction.
 Description de la vidéo
Description de la vidéo
Description à venir
Estimation
Estimer le résultat d’une opération, c’est en déterminer la valeur approximative par écrit ou mentalement. Les élèves éprouvent souvent de la difficulté avec l’estimation, car elles et ils ont du mal à reconnaître que plusieurs réponses peuvent être acceptables pour une situation donnée. Ainsi, il peut leur arriver, pour une estimation, de calculer la réponse exacte et de l’arrondir.
L’estimation est extrêmement utile dans les situations quotidiennes. Il peut même arriver qu’elle soit la seule réponse possible ou la réponse recherchée. Par exemple, en faisant des emplettes, on veut connaître le coût total de ses achats pour être en mesure de respecter son budget. Dans ce cas, on veut une idée approximative du résultat et non le coût total exact.
L’estimation sert souvent à donner un aperçu du résultat escompté ou à vérifier la vraisemblance de la solution. Les élèves doivent développer le réflexe d’effectuer mentalement une estimation rapide aussitôt qu’un calcul doit être effectué de manière à obtenir une idée générale du résultat. Malheureusement, plusieurs ne font pas le lien entre l’estimation et le résultat exact; l’estimation est alors perçue comme un autre calcul qu’il faut effectuer et non pas comme une stratégie réalisée informellement qui vient confirmer la vraisemblance du résultat du calcul.
Le personnel enseignant doit utiliser diverses stratégies d’enseignement pour faire prendre conscience aux élèves de la raison d’être de l’estimation. Par exemple, les élèves ne voient pas la pertinence de l’estimation si le résultat exact accompagne toujours l’estimation. Le personnel enseignant doit présenter des situations dont la solution du problème est une estimation ou des problèmes qui n’exigent pas une réponse précise (par exemple, déterminer la part de la dette nationale pour chaque citoyen ou faire les achats du matériel scolaire en prévision de l’an prochain).
Puisqu’au quotidien, les estimations sont souvent le fruit d’un calcul mental informel, il est donc normal que les élèves puissent s’y exercer et apprennent à estimer dans ce contexte. Le personnel enseignant devrait donc leur demander d’estimer le résultat d’une opération (sans utiliser papier et crayon) et de communiquer ce résultat approximatif (par exemple, \(346 + 516\), c’est près de 850).
Puisque le résultat d’une estimation représente une quantité approximative plutôt que précise, il ne devrait pas être communiqué exclusivement à l’aide d’un nombre (par exemple, au lieu d’affirmer que c’est 350, on peut dire que c’est environ 350). De plus, le résultat d’une estimation peut aider à indiquer l’ordre de grandeur ou l’envergure de la réponse (par exemple, ce sera au moins…, ce sera plus que…, la réponse doit être entre… et…, ou la réponse sera plus grande que…).
L’aptitude à estimer le résultat d’une opération est une caractéristique du sens des opérations. Elle manifeste une habileté à utiliser les nombres et les opérations de façon polyvalente. Pour estimer, les élèves utilisent une variété de stratégies basées sur leur sens du nombre et leur sens des opérations comme l’arrondissement, l’utilisation de repères, l’application des propriétés des opérations, la décomposition ou la compensation.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 92-94.
En 3e année, les élèves peuvent utiliser les stratégies d’estimation suivantes :
- Regroupement
Le regroupement est utile lorsque les nombres sont plus faciles à calculer. Le regroupement permet d’effectuer une addition répétée.
 Image Encadré qui donne un exemple de regroupement. Une addition verticale : 81 plus 37, plus 12,
plus 62 égal. On regroupe 80 et 12, on obtient un nombre près de cent. Ainsi que 37 et 62, on obtient un nombre près
de cent. La
réponse est près de 200
Image Encadré qui donne un exemple de regroupement. Une addition verticale : 81 plus 37, plus 12,
plus 62 égal. On regroupe 80 et 12, on obtient un nombre près de cent. Ainsi que 37 et 62, on obtient un nombre près
de cent. La
réponse est près de 200
- Les nombres pratiques
La stratégie des nombres pratiques consiste à utiliser les nombres qui sont faciles à manier. Dans l’addition et la soustraction, les élèves cherchent les nombres dont la somme ou la différence est près d’un multiple de 10.

- Estimation par la gauche
Dans ce type d’estimation, on effectue l’opération en se servant du chiffre de gauche. On peut ensuite obtenir une estimation plus précise en regardant le reste des nombres et en ajustant la réponse au besoin.
 Image Encadré qui donne un exemple d’estimation par la gauche : Une soustraction à la verticale.
763 moins 325 égal. On soustraie les centaines, 700 moins 300. Le reste des nombres indique que la réponse se situera
autour de 440.
Image Encadré qui donne un exemple d’estimation par la gauche : Une soustraction à la verticale.
763 moins 325 égal. On soustraie les centaines, 700 moins 300. Le reste des nombres indique que la réponse se situera
autour de 440.
- Arrondissement
L’arrondissement est une méthode d’estimation plus complexe que l’estimation par la gauche. Elle exige 2 étapes : d’abord arrondir chaque nombre, puis calculer l’estimation.
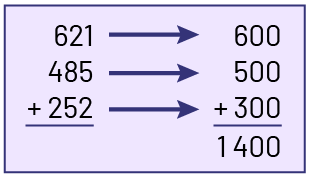 Image Encadré qui donne un exemple d’arrondissement : Une addition verticale : 621 plus, 485 plus,
252 égal. Les nombres de l’addition sont arrondis, on obtient : 600 plus, 500 plus, 300 égal 1400.
Image Encadré qui donne un exemple d’arrondissement : Une addition verticale : 621 plus, 485 plus,
252 égal. Les nombres de l’addition sont arrondis, on obtient : 600 plus, 500 plus, 300 égal 1400.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 69.
