At a Glance...

B2.3 Use mental math strategies, including estimation, to add and subtract whole numbers that add up to no more than 1000, and explain the strategies used.

Skill: Using Mental Math Strategies

---

Most of the calculations made on a daily basis are related to a mental calculation. People who acquire good mental math skills do not depend on electronics or paper to perform everyday calculations. However, it is important to demystify mental calculation. It is not about using an algorithm in your head, but about calculating with flexibility and efficiency.

A variety of instructional activities can be used to develop mental math skills. In all learning situations, teachers should take advantage of opportunities in mathematical exchanges to highlight the relationships among the different mental math strategies used by students. This highlights the similarities and differences between strategies, their strengths and weaknesses, and helps students make connections and learn other strategies.

Many mental math strategies are based on the relationship between the whole and its parts (partitioning and combining), on establishing relationships between numbers, and on the properties of operations. Often, these strategies come from a transfer of models used during the learning of operations.

Examples of Mental Math Strategies

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 111-112.

To facilitate the reading and understanding of this section, the operations are presented in the form of numerical expressions and models. In the classroom, when modelling strategies for students, teachers should represent operations horizontally, for example:

\(35 + 26\)

\(273 - 185\)

Addition

Using manipulatives is one of the first strategies students use to add. They can take objects from the classroom such as marbles, counters, or blocks to represent, for example, 86 + 56, and use counting strategies to find the sum. However, these strategies are not very effective with large numbers.

Addition of large numbers can be represented on a number line. For example, students could perform \(435 + 223\) by decomposing \(223 \ (200 + 15 + 8)\) and representing the operation as follows:

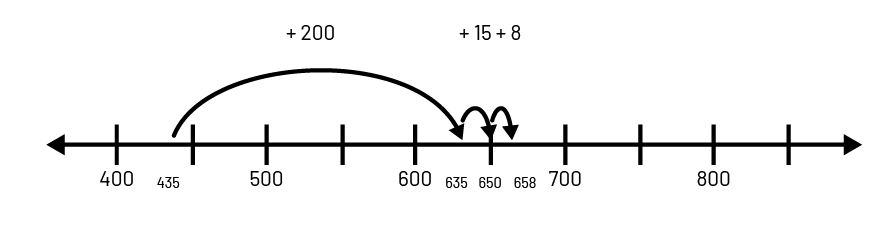
Over time, students gradually develop their sense of abstraction and can use the same strategy without using a number line, but by performing the calculation mentally.

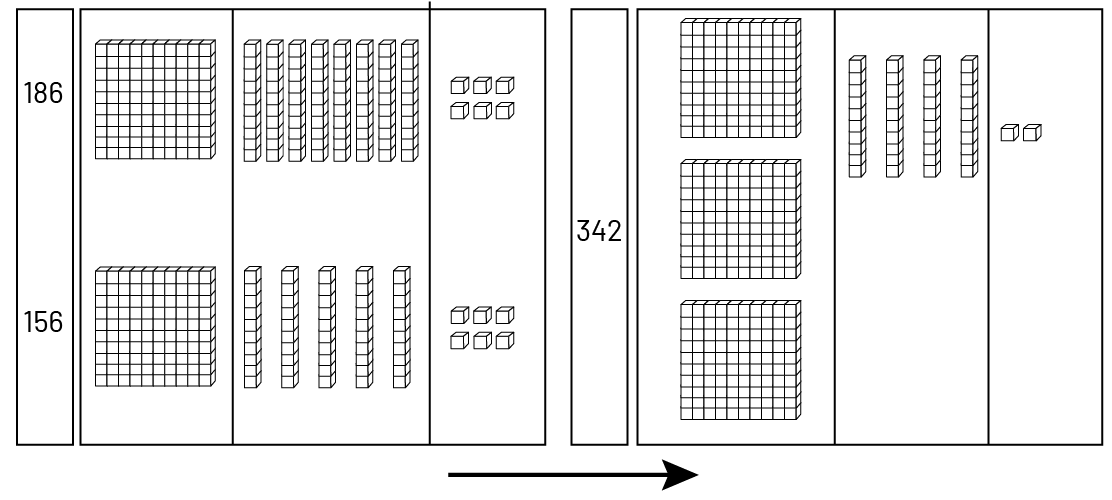
Base ten materials helps some students visualize the operation more clearly.

Here's how base ten materials can be used to represent addition.

Example

Students can also use a place value mat that organizes the material by the position of the digit in the number.

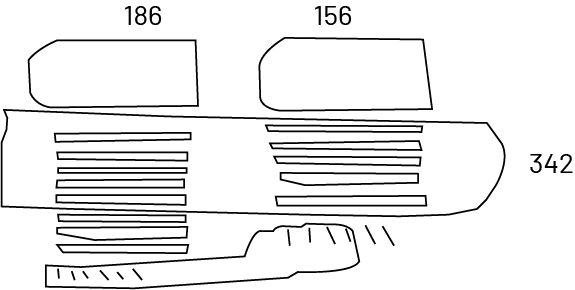
The same numeric expression (\(186 + 156\)) can be represented using drawings. In this way, students demonstrate a certain level of abstraction since a drawing is used to represent 100, 10 or 1.

Based on their experiences with numbers and algorithms, students can develop flexible algorithms. Some students may need to use pencil and paper to keep track of what they are doing, and this is acceptable. Examples of computational strategies for addition include:

Examples

\(378 + 123\)

• Add from left to right:

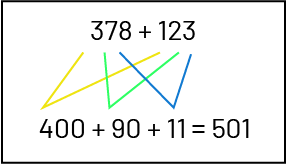
• Transform into friendlier numbers using compensation:

• Skip count using place value:

• Decompose one addend using place value and recompose it with the other:

• Rounding a number and compensating:

Subtraction

As with addition, students often use manipulatives to perform subtraction. This strategy helps them grasp the concept of separation, although it is not very effective when dealing with large numbers.

Base ten materials allow students to perform subtraction using separation.

Example

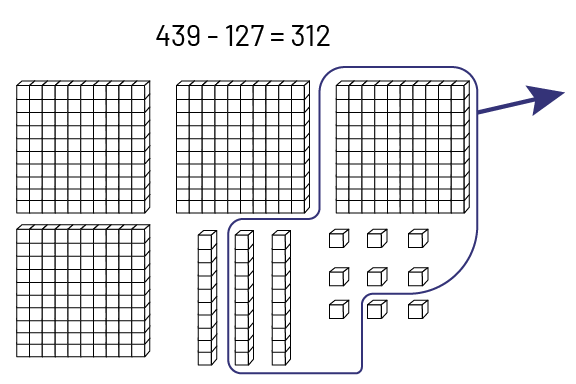
Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 121-128.

After experiencing various ways of representing operations, students have a better understanding of their respective uses. Examples of calculation strategies include:

Examples

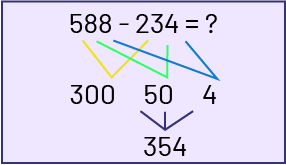
\(588 - 234\)

• Decompose numbers according to place value and perform partial subtractions:

• Rounding numbers, subtracting and compensating:

• Subtract beginning from the left:

• Decomposing and recomposing numbers:

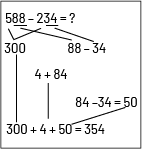
Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 130-131.

Estimation

Estimating the result of an operation means determining the approximate value of the operation in writing or mentally. Students often have difficulty with estimation because they have difficulty recognizing that more than one answer may be acceptable for a given situation. For example, to estimate, they may calculate the correct answer and then round it off.

Estimation is extremely useful in everyday situations. It may even be the only possible or desired answer. For example, when shopping, you want to know the total cost of your purchases to be able to stick to your budget. In this case, we want an approximate idea of the result, not the exact total cost.

Estimation is often used to provide a preview of the expected result or to check the reasonableness of the solution. Students need to develop the ability to make a quick mental estimation as soon as a calculation is to be performed in order to get a general idea of the result. Unfortunately, many students do not make the connection between the estimation and the correct result; the estimation is then seen as another calculation that must be performed and not as an informally performed strategy that confirms the reasonableness of the calculation.

Teachers should use a variety of instructional strategies to make students aware of the purpose of estimation. For example, students do not see the relevance of the estimation if the exact result always accompanies the estimation. Teachers should present situations where the solution of the problem is an estimation or problems that do not require a precise answer (for example, determining the share of the national debt for each citizen or making purchases of school materials in anticipation of next year).

Since on a daily basis, estimations are often the result of informal mental calculations, it is appropriate that students practice and learn to estimate in this context. Teachers should therefore ask them to estimate the result of an operation (without using paper and pencil) and to communicate this approximate result (for example, \(346 + 516\) is close to 850).

Because the result of an estimation represents an approximate rather than a precise quantity, it should not be communicated exclusively using a number (for example, instead of stating that it is 350, one can say that it is about 350). In addition, the result of an estimation can help indicate the order of magnitude or the scale of the answer (for example, it will be at least… , it will be more than…, the answer must be between…and…, or the answer will be greater than…).

The ability to estimate the result of an operation is a component of operational sense. It demonstrates an ability to use numbers and operations in a variety of ways. To estimate, students use a variety of strategies using their number and operational sense including rounding, benchmarks, applying properties of operations, decomposing, or compensating.

Source: translated from Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 92-94.

In Grade 3 , students may use the following estimation strategies:

• Clustering

Clustering is useful when numbers are easier to calculate. Clustering allows for repeated addition.

• Friendly or compatible Numbers

The compatible number strategy is to use numbers that are easy to work with. In addition and subtraction, students look for numbers whose sum or difference is near 10.

• Front-End Estimation

In this type of estimation, the operation is performed using the highest place value number, with an adjustment of the remaining values.

• Rounding

Rounding is a more complex estimation strategy than front-end estimation. It requires two steps: first rounding each number, then estimating.

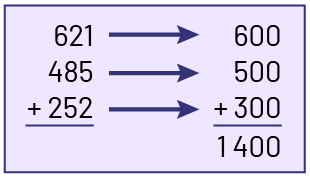
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6^e année, Fascicule 5, p. 69.