B2.6 Représenter la multiplication de nombres jusqu’à 10 × 10 et la division de nombres jusqu’à 100 ÷ 10, à l’aide d’une variété d’outils et de schémas, y compris des dispositions rectangulaires.
Habileté : représenter la multiplication et la division de nombres
L’élève qui arrive en 3e année a été exposé au concept de multiplication par le biais de l’addition répétée. Elle ou il sait intuitivement, par exemple, que 3 groupes de 2 pommes donnent 6 pommes. Cependant, elle ou il ne connaît ni le symbole ni le vocabulaire associé à ce type d’opération.
La multiplication consiste à combiner des ensembles égaux d’objets. Ceci permet d’établir une relation avec l’addition répétée. C’est par l’utilisation de matériel concret que l’élève arrive à découvrir et à comprendre le concept de multiplication. Par exemple, pour déterminer le nombre total d’éléments dans 3 ensembles comprenant 6 éléments chacun, l’élève représente la situation à l’aide de jetons et utilise diverses stratégies de dénombrement. Au début, elle ou il compte peut-être par 1 pour déterminer le total, mais avec un peu d’expérience, elle ou il apprend à utiliser des stratégies de dénombrement plus complexes telles que compter par intervalles ou utiliser l’addition répétée (par exemple, \(6 + 6 + 6\)). Finalement, elle ou il passe à la représentation symbolique de la multiplication en écrivant \(3 \times 6 = 18 \). Notons que même s’il importe que l’élève connaisse les tables de multiplication, ce n’est pas le but premier de l’apprentissage de la multiplication. Il est avant tout essentiel que l’élève saisisse le concept de multiplication avant d’apprendre les tables.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 185.
Au départ, la multiplication représente l’addition d’une même quantité répétée un certain nombre de fois. De façon abstraite, la multiplication est composée de 2 facteurs qui donnent un produit.
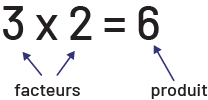
Pour bien assimiler la multiplication, les élèves doivent comprendre que les 2 facteurs ne jouent pas le même rôle. Fréquemment, une phrase mathématique comme \(3 \times 2 \) se lit « 3 fois 2 ». Dans cette interprétation, le facteur 3 représente 3 groupes, alors que le facteur 2 représente 2 éléments dans chaque groupe.
La même phrase mathématique \(3 \times 2 \) peut aussi être interprétée en utilisant les mots « multiplié par ». Alors \(3 \times 2 \) se lit « 3 multiplié par 2 », ce qui crée plutôt l’image de groupes de 3, 2 fois.
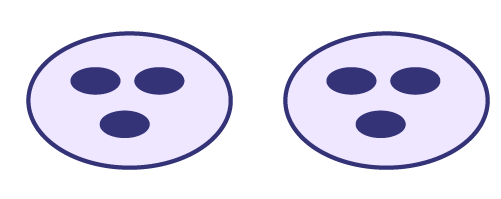
Ces 2 façons d’interpréter la phrase mathématique sont correctes. Le contexte d’où provient la phrase mathématique permettrait de préciser la représentation qui lui correspond.
Dans la division, une quantité est séparée en groupes égaux. Le dividende représente la quantité à partager alors que le diviseur et le quotient représentent respectivement le nombre de groupes et la taille des groupes si la division a le sens de partage ou l’inverse si la division a le sens de groupement.
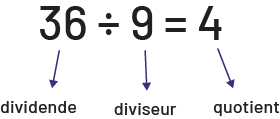
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 80-81.
La division a un sens de partage lorsque la quantité totale et le nombre de groupes sont connus (par exemple, 3 élèves veulent se partager équitablement 15 pommes et on cherche le nombre de pommes que chacun recevra).
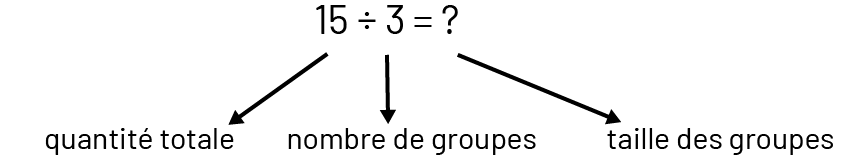
La division a un sens de groupement lorsque la quantité totale et le nombre d’éléments dans chaque groupe (taille des groupes) sont connus (par exemple, on a 15 pommes et on veut les placer dans des sacs, 3 pommes par sac; on cherche le nombre de sacs qu’il faut).
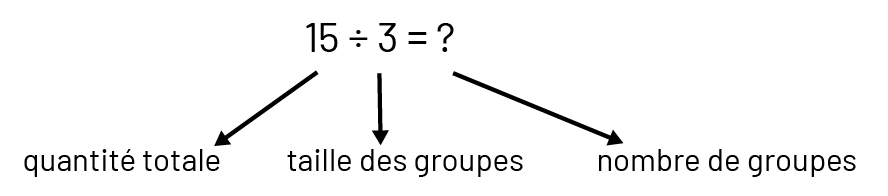
À mesure que les élèves progressent, il est important qu’ils y voient le concept de multiplication plutôt que celui d’addition et qu’elles et ils apprennent d’autres représentations. La disposition rectangulaire, un agencement de rangées et de colonnes, s’avère un modèle puissant dans l’apprentissage de la multiplication et de la division et permet de voir ces opérations sous un angle différent.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 85-86.
Le modèle de la disposition rectangulaire peut être présenté aux élèves de différentes façons. Dans le cadre d’un échange mathématique, par exemple, le personnel enseignant peut partir du travail d’une ou d’un élève et proposer une nouvelle organisation des objets en disposition rectangulaire.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 134.
Lorsqu’il s’agit d’une multiplication, on connaît le nombre de rangées et le nombre de colonnes. Pour la division, on connaît le nombre total ainsi que le nombre de rangées ou le nombre de colonnes. Pour organiser les objets dans une disposition rectangulaire, les objets sont placés dans des rangées ou des colonnes connues jusqu’à ce que tous les objets soient distribués de manière égale.
Source : adapté du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemples
- Il y a 4 gros biscuits sur chaque plateau. S’il y a 3 plateaux, combien y a-t-il de biscuits?
Image Trois fois quatre. « écrit en lettres » 3 multiplié par 4. Addition répétée. 4 plus 4 plus 4. Groupes égaux. 3 groupes de 4 éléments. Disposition rectangulaire. Une grille de 4 colonnes et 3 rangées.
- 12 biscuits ont été cuits. Si chaque plateau contient 4 biscuits, combien de plateaux faut-il?
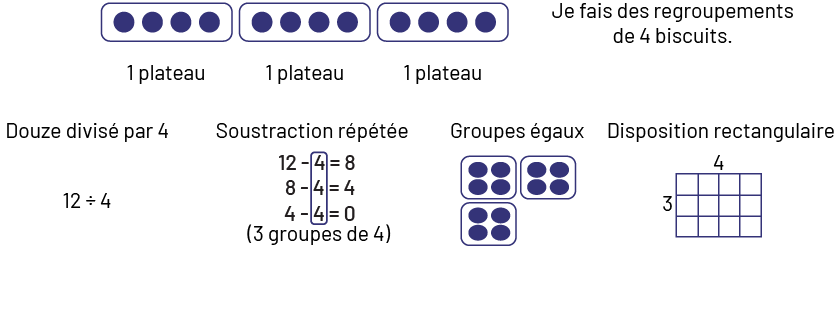Image Je fais des regroupements de 4 biscuits. 3 groupes de 4 biscuits. Chaque groupe représente un plateau. Douze divisé par 4 « écrit en lettres ». 12 divisé par 4. Soustraction répétée 12 moins 4 égale 8. 8 moins 4 égal 4. 4 moins 4 égale zéro (Parenthèse ouvrante) 3 groupes de 4 (parenthèse fermante). Groupes égaux. 3 groupes de 4 éléments. Disposition rectangulaire. 4 colonnes de 3 rangées.
- 12 biscuits ont été cuits. Si 3 plateaux étaient utilisés avec le même nombre de biscuits sur chaque plateau, combien y en avait-il sur chaque plateau?
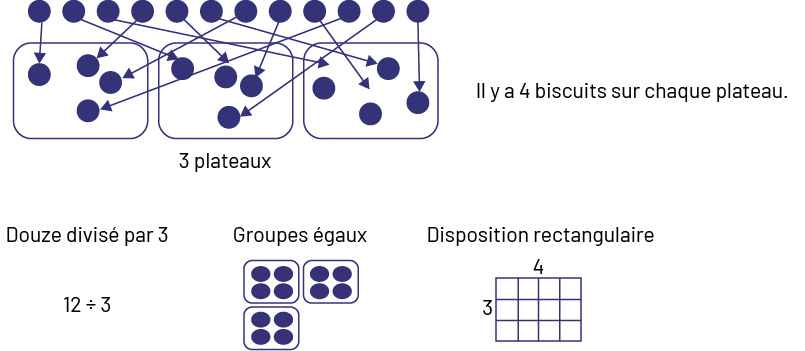Image 12 points représentent les 12 biscuits. Avec des flèches chaque biscuit est placé sur 3 plateaux. Il y a 4 biscuits sur chaque plateau. Douze divisé par 3 « écrit en lettre ». 12 divisé par 3. Groupes égaux. 3 groupes de 4 éléments. Disposition rectangulaire. 4 colonnes de 3 rangées.
Une disposition rectangulaire est un excellent modèle visuel pour représenter la commutativité de la multiplication.
Il est important de présenter ce modèle progressivement. Commencer par présenter des rangées et des colonnes d’objets familiers comme des fruits, des muffins, des chaises. Ensuite, illustrer avec des jetons. Poursuivre avec un tableau de rangées et colonnes pour finir par une disposition rectangulaire vide (sans ligne).
Voici un exemple qui illustre cette progression.
À la fruiterie, on vend des oranges à la caisse. Le marchand place 4 rangées de 7 oranges dans chaque caisse. Combien d’oranges y a-t-il dans chaque caisse?
Voici 3 façons d’illustrer ce problème en tenant compte de la progression pour illustrer les dispositions rectangulaires.
Image Un dessin d’une boite dans laquelle il y a 4 rangées de 7 oranges. Une illustration accompagne la phrase.Des jetons en 4 rangées de 7 jetons. Une illustration accompagne la phrase.Un tableau de 4 multiplié par 7 cases. Une illustration accompagne la phrase.
Réponse
Il y a 28 oranges dans chaque caisse.
En plaçant verticalement ces dispositions rectangulaires, le personnel enseignant peut amener les élèves à découvrir la propriété de la commutativité.
\(4 \times 7 = 7 \times 4 \)
On peut aussi faire ressortir la relation inverse de la multiplication et la division : \(28 \ \mathord{oranges} \div 4 \ \mathord{rangées} = 7 \) ou \(28 \ \mathord{oranges} \div 7 \ \mathord{rangées} = 4 \).
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Voici une discussion parmi des élèves par rapport à la disposition rectangulaire et la commutativité.
Image 3 élèves discutent autour d’une grille. Le premier élève dit : « Moi, je vois plutôt 3 rangées de 5, donc 3 multipliés par 5. » Le deuxième élève dit : « Je vois 5 rangées de 3, donc 5 multipliés par 3.» Le troisième élève dit : « Je vois 5 colles de 3 rangées qui peuvent aussi être représentées par 5 multipliées par 3.
»
La multiplication est distributive sur l’addition.
L’exemple suivant illustre comment on peut utiliser la distributivité pour calculer \(6 \times 8 \). Dans un cas, on décompose le facteur 8 pour obtenir \(5 + 3 \). On a alors \(6 \times (5 + 3) = (6 \times 5) + (6 \times 3) \). Dans l’autre cas, on décompose le facteur 6 pour obtenir \(3 + 3 \). On a alors \((3 + 3) \times 8 = (3 \times 8) + (3 \times 8) \).
Image Disposition rectangulaire de 6 multiplié par 8, il y a 6 rangées de 8 triangles. Disposition rectangulaire (parenthèse ouvrante) 6 multipliée par 5 (parenthèse fermante) plus (parenthèse ouvrante) 6
multiplié par 3 (parenthèse fermante). 6 rangées de 5 triangles et 6 rangées de 3 triangles. Disposition rectangulaire de (parenthèse ouvrante) 3 multiplié par 8 (parenthèse fermante) plus (parenthèse ouvrante)
3 multiplié par 8 (parenthèse fermante). 3 rangées de 8 triangles et 3 rangées de 8 triangles.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 104.
Il est possible de représenter la multiplication de diverses façons. Par exemple, \(5 \times 6 \) peut être représenté par 5 groupes de 6 jetons. Les jetons sont ensuite dénombrés afin de déterminer le résultat de l’opération.
La droite numérique est utile pour représenter par bonds le nombre de répétitions d’une quantité. Le nombre sur lequel s’arrête le dernier bond est le produit recherché. Par exemple, \(5 \times 6 \) :
Source : adapté du Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 132.
Le Rekenrek peut aussi être utilisé pour représenter \(5 \times 6 \). L’élève peut utiliser la propriété de la distributivité en décomposant le 6 en \(3 + 3 \), dont \((5 \times 3) + (5 \times 3) \) ou encore en utilisant la commutativité, soit \(6 \times 5 \) pour faire les doubles plus 1 groupe de 5, \((5 \times 5) + 5 \).
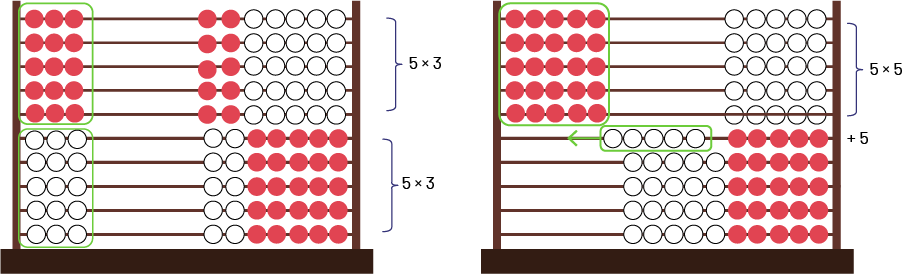Image Sur un Rekenrek : sur les dix tiges, les 3 premières boules sont placées sur la gauche. Les autres boules sont
sur la droite. Sur le côté du boulier, il y a une phrase mathématique qui accompagne les lignes du boulier : 5
multiplié par 3. Deuxième boulier chinois : pour les 5 premières lignes, les 5 premières boules sont placées sur la gauche. La phrase
mathématique suivante les accompagne : 5 multiplié par 5. Les 5 premières boules de la sixième ligne sont glissées vers la gauche : plus 5. Les boules des autres lignes sont
vers la droite du boulier.
Finalement, cette même multiplication peut aussi être représentée à l’aide d’une disposition rectangulaire. Par exemple, \(5 \times 6 \) est représenté par un rectangle de 5 rangées de 6 petits carrés. L’élève pourrait utiliser la propriété de la distributivité en décomposant le 6 en \(2 + 2 + 2 \), donc \((5 \times 2) + (5 \times 2) + (5 \times 2) \)
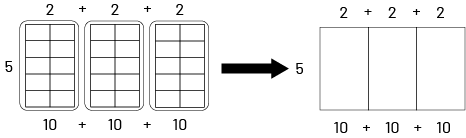Image 3 rectangles, divisés 10 parties égales, sur 2 colonnes et 5 rangées. Les phrases mathématiques suivantes accompagnent la représentation : 2 plus 2 plus 2. Dix plus dix plus dix. Une flèche pointe vers 3 autres rectangles vides. Les mêmes phrases mathématiques les accompagnent.
Connaissance : disposition rectangulaire
Les dispositions rectangulaires sont des outils très utiles pour développer le sens des opérations de multiplication et de division, et une compréhension de leurs propriétés. Il est possible de trouver divers exemples de dispositions rectangulaires (par exemple, calendrier, plateau de jeu de dames, carreaux du plancher) et de s’en servir en situation d’apprentissage.
Source : Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 2, Série 2, Activité 2 - Une visite au marché, p. 283.