B2.6 Represent multiplication of numbers up to 10 × 10 and division up to 100 ÷ 10, using a variety of tools and drawings, including arrays.
Skill: Representing Multiplication and Division
The student entering Grade 3 has been exposed to the concept of multiplication through repeated addition and equal groups. They know intuitively, for example, that 3 groups of 2 apples make 6 apples. However, they may not know the symbol or vocabulary associated with this type of operation.
Multiplication involves combining equal sets. This establishes a relationship with repeated addition. It is through the use of manipulatives that students come to discover and understand the concept of multiplication. For example, to determine the total number of elements in 3 sets of 6 elements each, the student represents the situation using counters and uses various counting strategies. At first, they may count by 1 to determine the total, but with some experience, they learn to use more complex counting strategies such as skip counting or using repeated addition (for example, \(6 + 6 + 6\)). Finally, the student moves on to the symbolic representation of multiplication by writing \(3 \times 6 = 18 \). Note that even if it is important for the student to know the multiplication tables, this is not the primary goal of learning multiplication. Above all, it is essential that the student grasp the concept of multiplication before learning the facts.
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 185.
Initially, multiplication represents the addition of the same quantity repeated a certain number of times. In an abstract way, multiplication is composed of two factors that give a product.
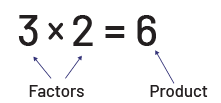
To properly assimilate multiplication, students must understand that the 2 factors do not play the same role. Frequently, a number sentence like \(3 \times 2 \) reads "3 times 2". In this interpretation, the factor 3 represents 3 groups, while the factor 2 represents 2 items in each group.

The same number sentence \(3 \times 2 \) can also be interpreted using the words "multiplied by". So \(3 \times 2 \) reads "3 multiplied by 2", which instead creates the image of groups of 3, twice.
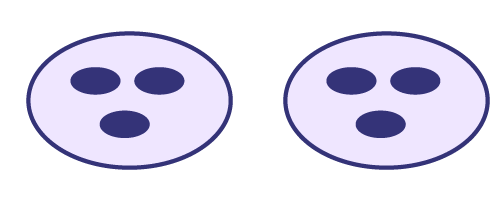
Both ways of interpreting the number sentence are correct. The context from which the number sentence comes should help to specify the representation that corresponds to it.
In division, a quantity is separated into equal groups. The dividend represents the quantity to be divided, while the divisor and quotient represent respectively the number of groups and the size of the groups if the division is partitive or, the opposite, if the division is quotative.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 80-81.
Division has a partitive meaning when the total quantity and the number of groups are known (for example, 3 students want to share 15 apples equally and we look for the number of apples each will receive).

Division has a quotative meaning when the total quantity and the size of groups are known (for example, we have 15 apples and we want to put them in bags, 3 apples per bag; we look for the number of bags needed).
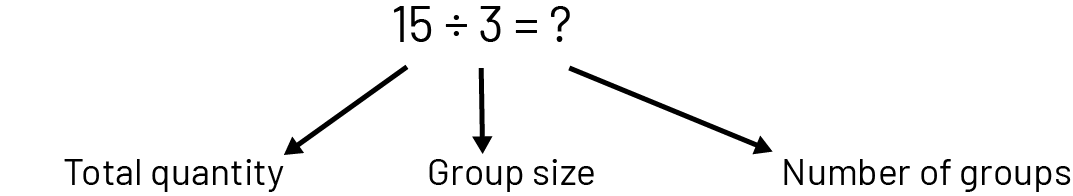
As students progress, it is important that they begin to see the concept of multiplication as more than repeated addition and learn other representations. The array is a powerful model for learning multiplication and division and provides a different perspective on these operations.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 85-86.
The array model can be introduced to students in a variety of ways. For example, during a math discussion, teachers can use a piece of student work as a starting point and propose organizing objects into an array.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 134.
For multiplication, the number of rows and the number of columns are known. In a division situation the total number of objects is known, as well as either the number of rows or the number of columns. To arrange the objects into an array, the objects are placed in known rows or columns until all objects are evenly distributed.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Examples
- There are 4 large cookies on each tray. If there are 3 trays, how many cookies are there?

- 12 cookies have been baked. If each tray contains 4 cookies, how many trays are needed?
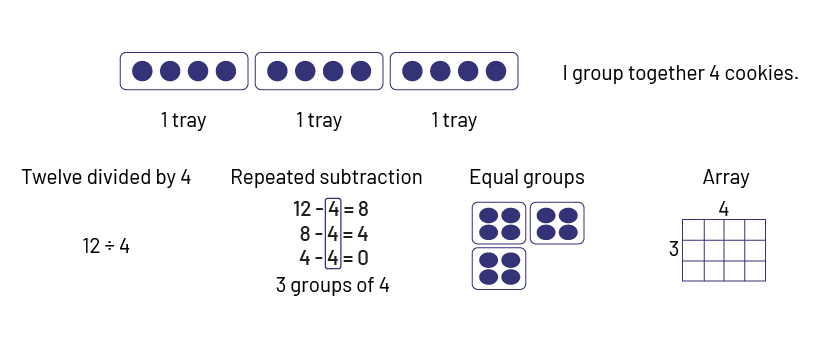
- 12 cookies were baked. If 3 trays were used with the same number of cookies on each tray, how many cookies were on each tray?

An array is an excellent visual model for representing the commutative property of multiplication.
It is important to introduce this model gradually. Begin by presenting rows and columns of familiar objects such as fruit, muffins, or chairs. Then illustrate with counters. Continue with an array of rows and columns and end with an open array as illustrated in the progression below.
At the fruit store, oranges are sold by the case. The merchant places 4 rows of 7 oranges in each case. How many oranges are in each case?
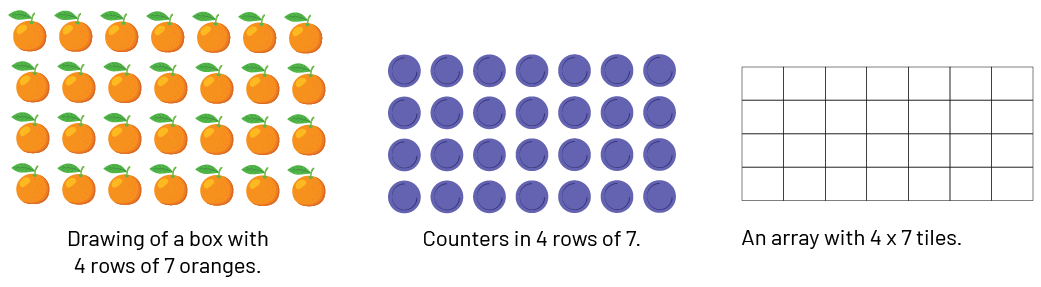
Answer
There are 28 oranges in each case.
By placing these arrays vertically, teachers can lead students to discover the commutative property.
\(4 \times 7 = 7 \times 4 \)
We can also highlight the inverse relationship of multiplication and division: \(28 \ \mathord{oranges} \div 4 \ \mathord{rows} = 7 \) or \(28 \ \mathord{oranges} \div 7 \ \mathord{rows} = 4 \).
Source: translated from L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Here is a discussion among students in relation to the array and commutative property.

Multiplication is distributive over addition.
The following example illustrates how the distributive property can be used to calculate \(6 \times 8 \). In one case, we decompose the factor 8 to obtain \(5 + 3 \). We then have \(6 \times (5 + 3) = (6 \times 5) + (6 \times 3) \). In the other case, we decompose the factor 6 to obtain \(3 + 3 \). We then have \((3 + 3) \times 8 = (3 \times 8) + (3 \times 8) \).

Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 104.
Multiplication can be represented in a variety of ways. For example, \(5 \times 6 \) can be represented by 5 groups of 6 counters. The counters are then counted to determine the result of the operation.
The number line is useful for representing the number of equal groups. The number at which the last jump ends is the total or product. For example, \(5 \times 6 \):

Source: adapted and translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 132.
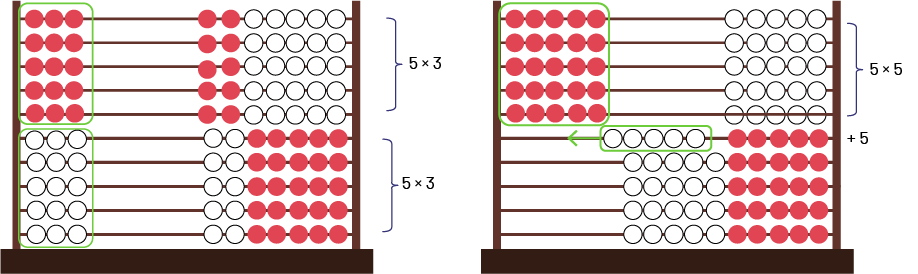
The Rekenrek can also be used to represent \(5 \times 6 \). The student can use the distributive property by decomposing the 6 into \(3 + 3 \), of which \((5 \times 3) + (5 \times 3) \) or by using the commutative property, that is \(6 \times 5 \) to make the doubles plus 1 group of 5, \((5 \times 5) + 5 \).
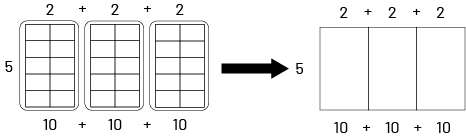
Finally, this same multiplication can also be represented using an array. For example, \(5 \times 6 \) is represented by a rectangle with 5 rows of 6 small squares. The student could use the distributive property by decomposing the 6 into \(2 + 2 + 2 \), so \((5 \times 2) + (5 \times 2) + (5 \times 2) \)
Knowledge: The Array
Arrays are very useful tools for developing a sense of multiplication and division and an understanding of their properties. Various examples of arrays (for example, calendar, checkerboards, floor tiles) can be found and used in learning situations.
Source: translated from Les mathématiques…un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 2, Série 2, Activité 2 - Une visite au marché, p. 283.
