B2.7 Représenter et résoudre des problèmes relatifs à la multiplication et à la division, y compris des problèmes comprenant des groupes d’un demi, d’un tiers et d’un quart, à l’aide d’outils et de schémas.
Habileté : représenter et résoudre des problèmes relatifs à la multiplication et à la division
L’apprentissage des opérations mathématiques s’effectue progressivement. Le point de départ devrait être l’exploration des opérations en situation de résolution de problèmes. Les élèves apprennent à associer des situations à des opérations particulières, ce qui leur permet de commencer à donner un sens aux opérations. De plus, les élèves doivent utiliser des stratégies basées sur leur compréhension du contexte, du problème et des opérations. Elles et ils prennent conscience qu’il existe plusieurs façons de résoudre un problème et même plusieurs façons d’effectuer la même opération. Par la suite, les élèves sont invités à résoudre une variété de problèmes afin de progresser vers l’utilisation de stratégies efficaces.
Contrairement à la démarche traditionnelle où les élèves apprennent surtout à appliquer les algorithmes usuels, l’apprentissage des opérations doit davantage être orienté vers la compréhension des opérations, l’exploration du calcul mental et l’utilisation de diverses stratégies pour effectuer les opérations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 75-76.
Effet des opérations
Chaque opération produit un effet sur les quantités en cause. Selon l’opération, certaines quantités augmentent ou diminuent. Elles peuvent augmenter ou diminuer de beaucoup ou de peu. Suivre l’effet des opérations sur les nombres permet aux élèves d’établir les liens entre les opérations et d’anticiper le résultat d’une opération. Par exemple, si on soustrait 8 de 160, on remarquera peu d’effet, car la différence entre 160 et 152 est relativement petite. Cependant, si on divise 160 par 8, l’effet produit est grand, car le quotient obtenu, soit 20, est beaucoup plus petit que 160.
Une mise en garde s’impose : il faut faire preuve de prudence lorsqu’on généralise, car les opérations sur les nombres décimaux ou les fractions peuvent avoir des effets différents que ceux sur les nombres naturels. Dans certains cas, l’effet peut même être l’inverse.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 90-91.
Dans la division, une quantité est séparée en groupes égaux. Le dividende représente la quantité à partager alors que le diviseur et le quotient représentent respectivement le nombre de groupes et la taille des groupes si la division a le sens de partage ou l’inverse si la division a le sens de groupement.
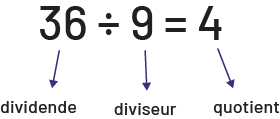
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 81.
Dans les problèmes présentés aux élèves, on associe trop souvent la division à un seul sens, soit le partage. Le sens de groupement est habituellement négligé. La division a un sens de partage lorsque la quantité totale et le nombre de groupes sont connus (par exemple, 3 élèves veulent se partager équitablement 15 pommes et on cherche le nombre de pommes que chacun recevra).
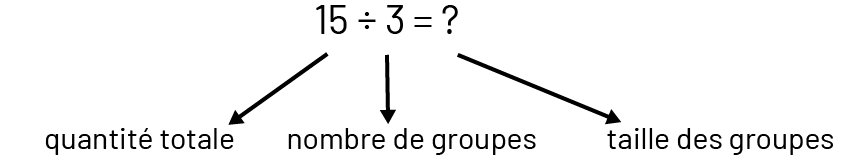
La division a un sens de groupement lorsque la quantité totale et le nombre d’éléments dans chaque groupe (taille des groupes) sont connus (par exemple, on a 15 pommes et on veut les placer dans des sacs, 3 pommes par sac; on cherche le nombre de sacs qu’il faut).
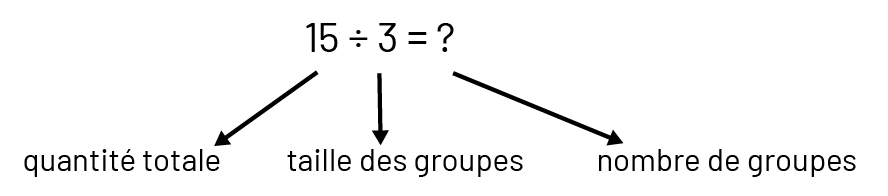
Il est essentiel de traiter des 2 types de problèmes, puisqu’ils sont la base de l’intégration d’autres concepts mathématiques. Il n’est pas nécessaire que les élèves sachent le nom des types de problèmes, mais il est essentiel qu’elles et ils aient l’occasion d’en résoudre de divers types, tout en employant une variété de stratégies.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 86.
Problèmes écrits relatifs à la multiplication et à la division
Les élèves acquièrent une bonne compréhension de la multiplication et de la division ainsi que des relations entre les nombres en résolvant des problèmes écrits. Les types de problèmes de groupes égaux présentés ci-après à l’aide d’exemples peuvent aider les élèves à percevoir les faits numériques de base relatifs à la multiplication et à la division de diverses façons. Le recours aux problèmes pour présenter les faits numériques de base oblige les élèves à raisonner pour trouver des solutions et permet ainsi de développer un meilleur sens des opérations.
Les exemples de problèmes écrits ci-dessous contiennent des nombres d’un chiffre. Les structures des 3 types de problèmes écrits se prêtent aussi aux nombres à plusieurs chiffres. Les problèmes sont représentés à l’aide de réglettes Cuisenaire.
Problèmes de groupes égaux
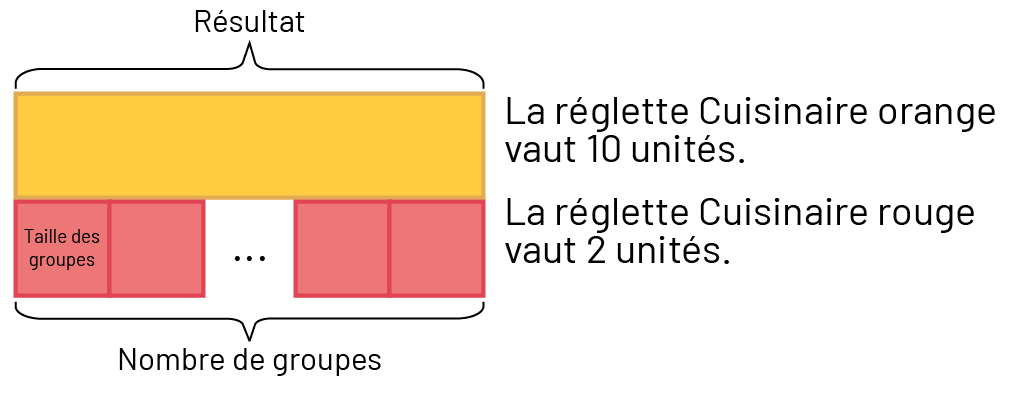 Image La réglette Cuisinaire orange vaut dix unités. La réglette Cuisinaire rouge vaut 2 unités.
Les phrases ci-dessus sont illustrées. Une réglette Cuisinaire orange représente le résultat. 4 réglettes Cuisinaire
rouges sont placées deux par deux aux
extrémités de la réglette orange, il y a un espace vide entre les groupes de deux. Sur la première réglette rouge, on
peut lire « taille des groupes ». Les réglettes rouges représentent le nombre de groupes.
Image La réglette Cuisinaire orange vaut dix unités. La réglette Cuisinaire rouge vaut 2 unités.
Les phrases ci-dessus sont illustrées. Une réglette Cuisinaire orange représente le résultat. 4 réglettes Cuisinaire
rouges sont placées deux par deux aux
extrémités de la réglette orange, il y a un espace vide entre les groupes de deux. Sur la première réglette rouge, on
peut lire « taille des groupes ». Les réglettes rouges représentent le nombre de groupes.
- Groupes égaux : tout inconnu (multiplication)
Julie a acheté 5 livres pour ses camarades. Chaque livre lui a coûté 2,00 $. Combien Julie a-t-elle dépensé pour tous ces livres?
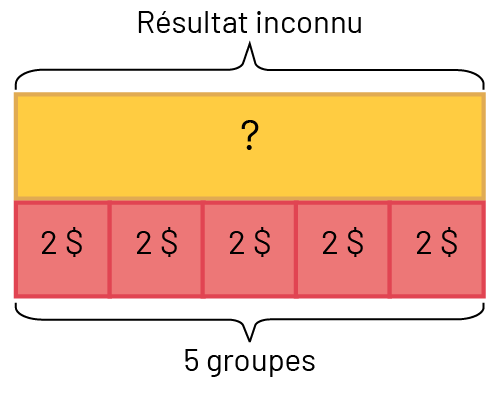 Image La réglette Cuisinaire orange a une valeur inconnue. « Résultat inconnu ». En dessous 5
réglettes rouges dont la valeur unitaire est de 2 dollars. « 5 groupes ».
Image La réglette Cuisinaire orange a une valeur inconnue. « Résultat inconnu ». En dessous 5
réglettes rouges dont la valeur unitaire est de 2 dollars. « 5 groupes ».
\(2 + 2 + 2 + 2 + 2 = \mathord{?} \) ou \(5 \times 2 = \mathord{?} \)
- Groupes égaux : nombre de groupes inconnu (répartition égale)
Julie a acheté 10 livres pour ses camarades et prépare des sacs-cadeaux. Elle met 2 livres dans chaque sac. Combien de sacs-cadeaux Julie a-t-elle utilisés?
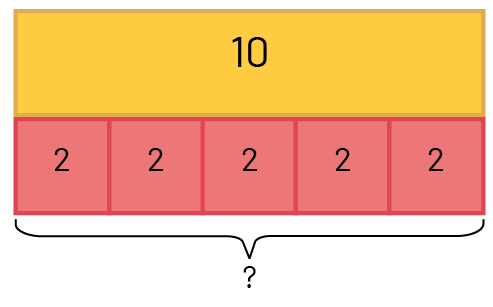
 Image Des additions sont alignées les unes au-dessus des autres. 2 plus 2 égal 4. 4 plus 2 égal
6. 6 plus 2 égal 8. 8 plus 2 égal dix. Tous les 2 sont encerclés pour créer un ensemble. Le commentaire suivant
accompagne les phrases mathématiques. «
J’ai additionné 2 à 5 reprises. J’ai additionné 2 à 5 reprises.
Image Des additions sont alignées les unes au-dessus des autres. 2 plus 2 égal 4. 4 plus 2 égal
6. 6 plus 2 égal 8. 8 plus 2 égal dix. Tous les 2 sont encerclés pour créer un ensemble. Le commentaire suivant
accompagne les phrases mathématiques. «
J’ai additionné 2 à 5 reprises. J’ai additionné 2 à 5 reprises.
ou \(10 \div 2 = \mathord{?} \) ou \(\mathord{?} \times 2 = 10 \)
- Groupes égaux : taille des groupes inconnue (partage)
Julie a 10 livres. Elle veut les donner à 5 de ses camarades. Combien de livres recevra chaque camarade?
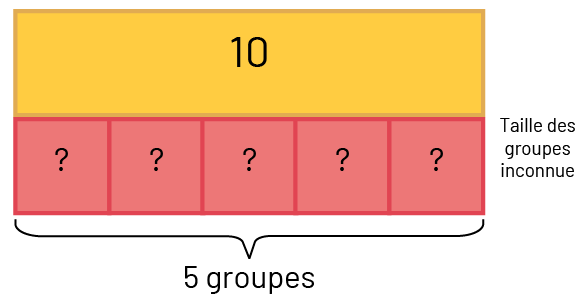
\(10 \div 5 = \mathord{?} \) ou \(5 \times \mathord{?} = 10 \)
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10-11.
La relation inverse de la division et de la multiplication
De façon analogue, les élèves peuvent développer leur compréhension du fait que la multiplication et la division sont des opérations inverses (par exemple, \(4 \times 5 = 20 \) et \(20 \div 5 = 4 \)). Les élèves peuvent faire diverses activités pour développer leur compréhension de la multiplication en tant qu’additions répétées (par exemple, \(3 \times 7 \) donne le même résultat que \(7 + 7 + 7\)) et de la division en tant que soustractions répétées ou additions répétées (par exemple, \(24 \div 6 \) peut être déterminé en observant qu’il est possible d’effectuer, à partir de 24, 4 soustractions successives de 6 ou qu’il est possible d’effectuer, à partir de 0, 4 additions successives de 6 pour arriver à 24).
Les élèves peuvent effectuer diverses activités pour découvrir les principales propriétés de chacune des opérations. Par exemple, elles et ils peuvent combiner 5 ensembles de 4 cubes et 4 ensembles de 5 cubes et constater que le résultat est le même (\(5 \times 4 = 4 \times 5 \); propriété de la commutativité de la multiplication). La compréhension de cette propriété peut faciliter, entre autres, l’apprentissage des faits numériques de base.
Au fur et à mesure que les élèves acquièrent une bonne compréhension des opérations arithmétiques de base, elles et ils sont en mesure d’utiliser les liens entre ces opérations pour résoudre des problèmes. Ainsi, pour diviser également 12 bonbons, elles et ils peuvent utiliser diverses stratégies basées sur l’une ou l’autre des opérations, par exemple :
- 2 ensembles de 6 bonbons puisque \(12 \div 6 = 2 \);
- 6 ensembles de 2 bonbons puisque \(6 \times 2 = 12 \);
- 3 ensembles de 4 bonbons puisqu’on peut retirer 4 bonbons 3 fois à partir de l’ensemble de 12 bonbons \((12 - 4 - 4 - 4)\) et qu’il ne restera aucun bonbon;
- 4 ensembles de 3 bonbons puisque \(3 + 3 + 3 + 3 = 12 \).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 62-63.
Multiplication — Stratégies
Voici une panoplie de stratégies qui peuvent être utilisées pour effectuer la multiplication. Elles répondent à des besoins variés et facilitent l’apprentissage des élèves.
Exemple 1
Le père d’Amélie lui annonce que sa cousine Milène, du Manitoba, vient en visite sous peu. Son père lui a dit qu’il reste 5 semaines avant son arrivée. Combien de jours reste-t-il avant que Milène arrive?
une semaine = 7 jours
\(7 \times 5 = \mathord{?} \)
Distributivité à l’aide de la disposition rectangulaire
Je décompose 7 en \(5 + 2 \), dont \((5 \times 5) + (5 \times 2)\).
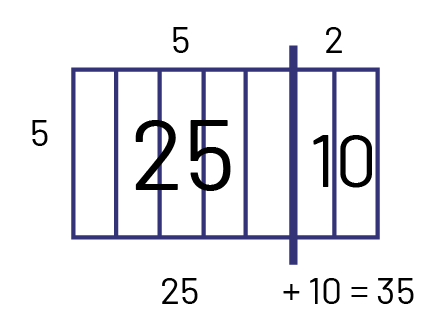 Image Une disposition rectangulaire qui décompose 7, donc 5 barres d’un bord et 2 de l’autre.
Chaque barre a une
valeur de 5 donc l’ensemble de 5 barres vaut 25 et l’ensemble de 2 barres vaut dix. 25 plus dix égal 35. Je peux donc
dire maintenant qu’il reste 35 jours avant que Milène arrive.
Image Une disposition rectangulaire qui décompose 7, donc 5 barres d’un bord et 2 de l’autre.
Chaque barre a une
valeur de 5 donc l’ensemble de 5 barres vaut 25 et l’ensemble de 2 barres vaut dix. 25 plus dix égal 35. Je peux donc
dire maintenant qu’il reste 35 jours avant que Milène arrive.
Exemple 2
Une planche à roulettes a 4 roues. Combien de roues ont 8 planches à roulettes?
\(8 \times 4 = \mathord{?} \)
Stratégie 1
Distributivité en décomposant à l’aide d’une droite numérique
Pour simplifier, je décompose le 8 en \(4 + 4 \). Alors je peux faire la multiplication suivante : \((4 \times 4) + (4 \times 4)\).
En 4 bonds de 4, j’arrive à 16.

Maintenant que je sais que \(4 \times 4 = 16 \), je répète l’opération 2 fois, soit : 16 + 16 = 32.
Alors, 8 planches à roulettes ont 32 roues.
Stratégie 2
Distributivité à l’aide du Rekenrek
Je vais faire la multiplication \(4 \times 8 \) avec le Rekenrek, car j’aurai le même résultat que \(8 \times 4 \). Je place donc 8 perles à la gauche du Rekenrek sur les 4 premières lignes. Je constate qu’il y a alors 4 tiges de 5 perles et 4 tiges de 3 perles. Je peux calculer plus facilement maintenant ces 2 multiplications, puisque 4 groupes de 5 perles font \(4 \times 5 = 20 \), et 4 groupes de 3 perles font \(4 \times 3 = 12 \).
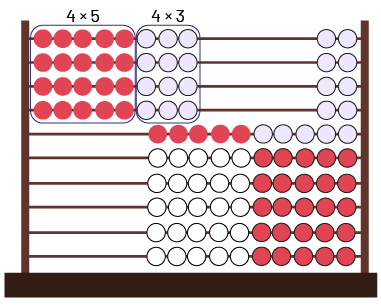 Image Sur un Rekenrek. Les 4 premières lignes de boules, ont 5 boules rouges et 3 boules blanches
de placées sur la gauche, les boules
rouges forment un ensemble : 4 multiplié par 5. Et les boules blanches forment un autre ensemble : 4 multiplié par 3.
Il me suffit enfin d’additionner 20 et 12. Je combine les dizaines \((20 + 10) + 2 = 32\). Il y a donc 32 roues sur
8 planches à roulettes.
Image Sur un Rekenrek. Les 4 premières lignes de boules, ont 5 boules rouges et 3 boules blanches
de placées sur la gauche, les boules
rouges forment un ensemble : 4 multiplié par 5. Et les boules blanches forment un autre ensemble : 4 multiplié par 3.
Il me suffit enfin d’additionner 20 et 12. Je combine les dizaines \((20 + 10) + 2 = 32\). Il y a donc 32 roues sur
8 planches à roulettes.
Source des problèmes : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Exemple 3
Sylvie achète 6 boîtes de biscuits. Un tiers des biscuits de chaque boîte est au beurre d’arachides. Combien de boîtes de biscuits sont au beurre d’arachides?
Source du problème : adapté du CFORP, Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 2, Série 2, Minileçon 4 - Des fractions en devinettes, p. 347.
Stratégie 1
Addition répétée à l’aide d’une droite numérique
Je sais que les biscuits au beurre d’arachides représentent \(\frac{1}{3} \) de chaque boîte et qu’il y a 6 boîtes en tout.
Je peux donc dire que cela correspond à l’addition répétée suivante :
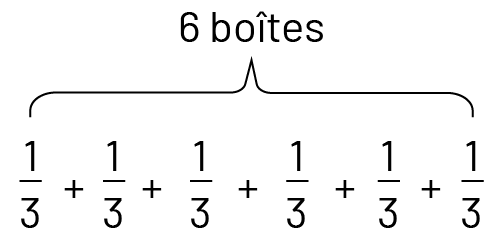
J’ai donc 6 groupes de \(\frac{1}{3} \), que je peux écrire \(6 \times \frac{1}{3} \).
Pour m’aider, je représente les 6 bonds de \(\frac{1}{3} \) sur une droite numérique.
\(\frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3}\)
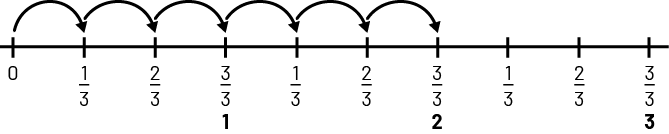
= 6 un tiers ou 2
Il y a donc \(6 \times \frac{1}{3} \) de biscuits au beurre d’arachides, ce qui correspond à 2 boîtes.
Stratégie 2
Addition répétée à l’aide d’un schéma
Pour compter le nombre de tiers, je vais représenter les 6 un tiers de chaque boîte dans un schéma et faire des regroupements de 3 un tiers de boîtes pour former des nombres entiers.
Les 3 premiers tiers de biscuits au beurre d’arachides forment 1 entier. Les 3 suivants forment un autre entier. Cela fait 2 boîtes de biscuits au beurre d’arachides des 6 boîtes de biscuits.
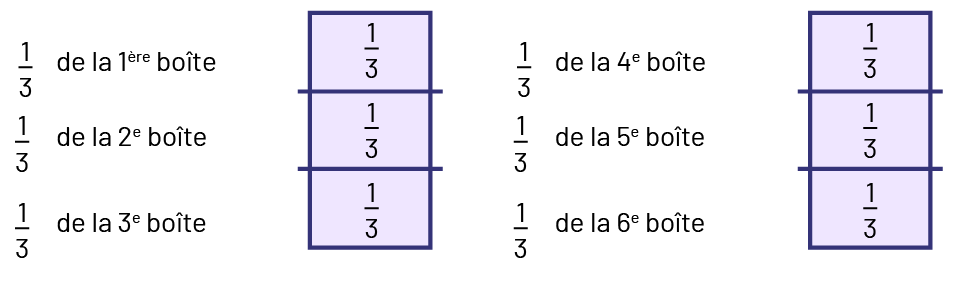 Image Un rectangle est divisé en 3 parties égales. Dans chaque partie on peut lire un tiers écrit
sous forme de
fraction. Un deuxième rectangle est semblable au premier. Un tiers de la première boite. Un tiers de la deuxième
boite. Un tiers de la troisième boite. Un tier de la quatrième boite. Un tiers de la cinquième boite. Un tiers de la
sixième boite.
Image Un rectangle est divisé en 3 parties égales. Dans chaque partie on peut lire un tiers écrit
sous forme de
fraction. Un deuxième rectangle est semblable au premier. Un tiers de la première boite. Un tiers de la deuxième
boite. Un tiers de la troisième boite. Un tier de la quatrième boite. Un tiers de la cinquième boite. Un tiers de la
sixième boite.
Source : adapté du En avant, les maths!, 3e année, CM, Nombres, p. 5-6.
Division (stratégies)
Exemple 1
C’est le temps de l’inscription pour les cours de natation. 72 enfants se sont inscrits. Les groupes sont formés de 8 enfants. Combien de groupes y aura-t-il?
Stratégie 1
Soustraction répétée à l’aide de la grille de 100
Je sais qu’il y a au total 72 enfants et que les groupes sont formés de 8 enfants. Je vais effectuer des soustractions répétées en représentant mes groupes dans une grille de 100.
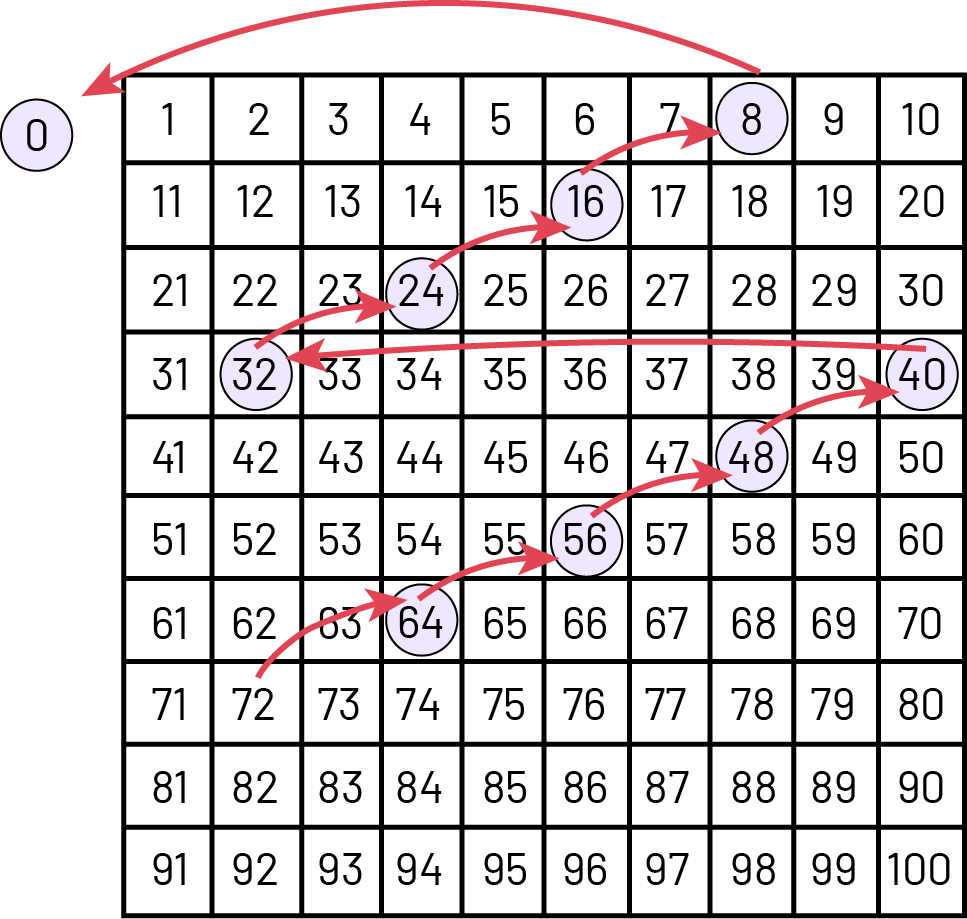 Image Soustractions répétées, illustrées avec une grille de cent. Les résultats des
soustractions sont encerclés dans la grille et une flèche rouge représente « pour chaque
soustraction » le bond en arrière de moins 8. 72 moins 8 égal 64. 64 moins 8 égal 56. 56 moins 8 égal 48. 48 moins 8
égal 40. 40 moins 8 égal 32. 32 moins 8 égal 24. 24 moins 8 égal 16. 16 moins 8 égal 8. 8 moins 8 égal zéro.
Image Soustractions répétées, illustrées avec une grille de cent. Les résultats des
soustractions sont encerclés dans la grille et une flèche rouge représente « pour chaque
soustraction » le bond en arrière de moins 8. 72 moins 8 égal 64. 64 moins 8 égal 56. 56 moins 8 égal 48. 48 moins 8
égal 40. 40 moins 8 égal 32. 32 moins 8 égal 24. 24 moins 8 égal 16. 16 moins 8 égal 8. 8 moins 8 égal zéro.
\(72 - 8 = 64\)
\(64 - 8 = 56\)
\(56 - 8 = 48\)
\(48 - 8 = 40\)
\(40 - 8 = 32\)
\(32 - 8 = 24\)
\(24 - 8 = 16\)
\(16 - 8 = 8\)
\(8 - 8 = 0\)
Maintenant que j’ai effectué mes soustractions répétées dans la grille de 100, il me suffit de compter la quantité de nombres entourés qui représentent le nombre de groupes d’enfants.
Je constate qu’il y a 9 nombres entourés dans la grille de 100. Il y a donc 9 groupes de 8 enfants.
Stratégie 2
Division à l’aide d’une disposition rectangulaire
Je fais ma disposition rectangulaire en faisant des rangées de 8. Je sais que \(5 \times 8 = 40 \), alors je fais 5 rangées. Je soustrais 40 de 72, ce qui me donne 32. Je sais que \(4 \times 8 = 32 \), alors j’ajoute 4 autres rangées de 8.
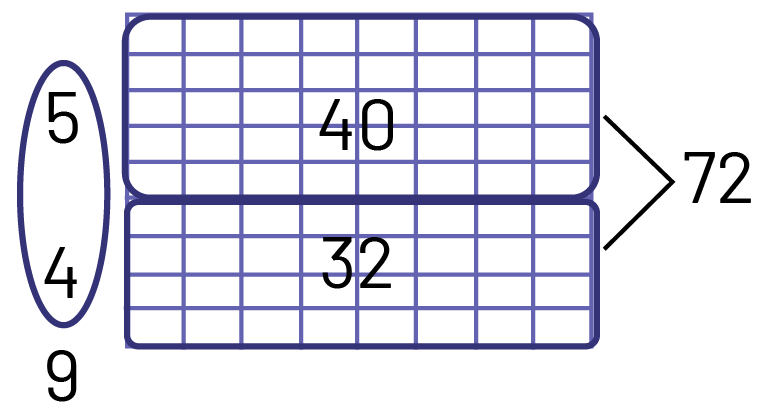 Image Disposition rectangulaire. De 5 rangées de 8 éléments pour un total de 40 éléments, ainsi
que 4 rangées de 8 éléments pour un total de 32
éléments. En additionnant tous les éléments, on en obtient 72.
Image Disposition rectangulaire. De 5 rangées de 8 éléments pour un total de 40 éléments, ainsi
que 4 rangées de 8 éléments pour un total de 32
éléments. En additionnant tous les éléments, on en obtient 72.
J’additionne le nombre de rangées, soit \(5 + 4 = 9 \). Il y a donc 9 groupes de 8 enfants.
Stratégie 3
Division à l’aide de la droite numérique double
J’ai placé 7 réglettes Cuisenaire orange (70) et une réglette rouge (2) au-dessus de la droite numérique double. Ceci représente les 72 enfants.
Ensuite, j’ai placé des réglettes brunes qui valent 8 unités chacune, jusqu’à ce que je me rende à 72. J’ai placé 9 réglettes brunes.
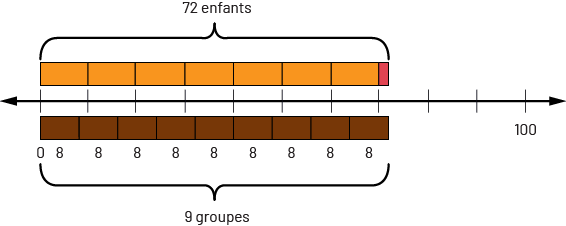 Image Une droite numérique de zéro à 100, par intervalles réguliers de 8. Sept réglettes Cuisinaire orange sont
placées au-dessus de la droite, elles représentent 70. Au bout, des réglettes orange, est placée une réglette rouge
qui représente 2. Il y a un total de 72 enfants. En dessous de la droite sont placées 9 réglettes brunes. Ceci
représente 9 groupes. Il y a donc 9 groupes de 8 enfants.
Image Une droite numérique de zéro à 100, par intervalles réguliers de 8. Sept réglettes Cuisinaire orange sont
placées au-dessus de la droite, elles représentent 70. Au bout, des réglettes orange, est placée une réglette rouge
qui représente 2. Il y a un total de 72 enfants. En dessous de la droite sont placées 9 réglettes brunes. Ceci
représente 9 groupes. Il y a donc 9 groupes de 8 enfants.
Exemple 2
Le personnel enseignant remet \(\frac{1}{4} \) d’une feuille de papier à 15 élèves dans sa classe afin qu’elles et ils écrivent une petite devinette. Combien de feuilles de papier le personnel enseignant a-t-il utilisées?
Stratégie
Division à l’aide d’une disposition rectangulaire et du regroupement
J’ai utilisé la disposition rectangulaire pour représenter les 15 élèves.
Je sais qu’il y a quatre \(\frac{1}{4} \) dans une feuille de papier. J’encercle quatre \(\frac{1}{4} \), ce qui me donne une pleine feuille de papier.
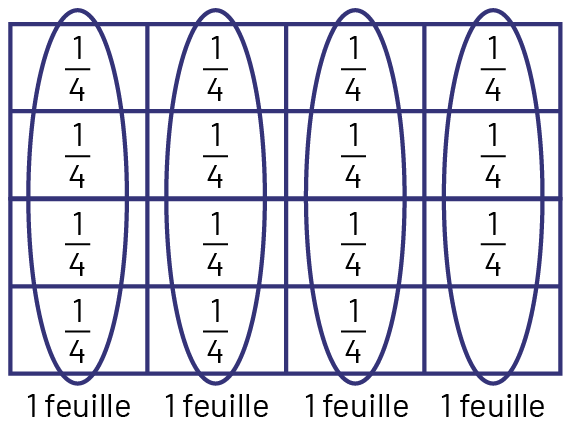 Image Exemple de disposition rectangulaire pour représenter 15 élèves. 4 feuilles de papier sont
divisées en 4 parties égales. Sur 15 parties on peut lire la fraction : un quart. Elles
sont encerclées 4 par 4.
Image Exemple de disposition rectangulaire pour représenter 15 élèves. 4 feuilles de papier sont
divisées en 4 parties égales. Sur 15 parties on peut lire la fraction : un quart. Elles
sont encerclées 4 par 4.
Le personnel enseignant a besoin de 4 feuilles de papier. Cependant, il va lui rester \(\frac{1}{4} \) de la dernière feuille.
Connaissance : problèmes de groupes égaux
Ce sont des problèmes qui impliquent des ensembles de quantité égale. Avec ces problèmes, il y a un groupe d’une taille donnée, qui est répété un certain nombre de fois pour arriver à un résultat. Parfois, la taille de chaque groupe est inconnue, parfois le nombre de groupes est inconnu et parfois le résultat est inconnu.
