B2.7 Represent and solve problems involving multiplication and division, including problems that involve groups of one half, one fourth, and one third, using tools and drawings.
Skill: Representing and Solving Problems Involving Multiplication and Division
The learning of mathematical operations takes place gradually. The starting point should be the exploration of operations in problem-solving situations. Students learn to associate situations with particular operations, which allows them to begin to make sense of the operations. In addition, students need to use strategies based on their understanding of the context, the problem and the operations. They become aware that there are many ways to solve a problem and even many ways to perform the same operation. Subsequently, students are asked to solve a variety of problems in order to progress towards using effective strategies.
In contrast to the traditional approach where students learn primarily to apply standard algorithms, operations learning should be more oriented toward understanding operations, exploring mental calculations, and using various strategies to perform operations.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 75-76.
Effect of Operations
Each operation has an effect on the quantities involved. Depending on the operation, certain quantities increase or decrease. They may increase or decrease by a lot or a little. Tracking the effect of operations on numbers allows students to make connections between operations and to anticipate the result of an operation. If, for example, 8 is subtracted from 160, little effect will be noticed because the difference between 160 and 152 is relatively small. However, if we divide 160 by 8, the effect is large, because the resulting quotient, 20, is much smaller than 160.
One caveat is that care must be taken when generalizing, because operations on decimal numbers or fractions may have different effects than operations on whole numbers. In some cases, the effect may even be the opposite.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 90-91.
In division, a quantity is separated into equal groups. The dividend represents the quantity to be divided, while the divisor and quotient represent respectively the number of groups and the size of the groups if the division is partitive or, the opposite, if the division is quotative.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 81.
In problems presented to students, division is too often associated with only one of its meanings, namely equal sharing (partitive division). The equal grouping meaning (quotative division) is usually neglected. Division has a partitive meaning when the total quantity and the number of groups are known (for example, 3 students want to share 15 apples equally and we are looking for the number of apples each person will receive).
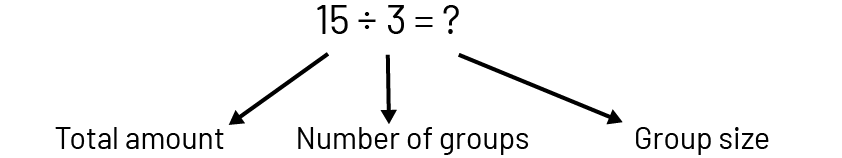
Division has a quotative meaning when the total quantity and the size of groups are known (for example, we have 15 apples and we want to put them in bags, 3 apples per bag; we look for the number of bags needed).
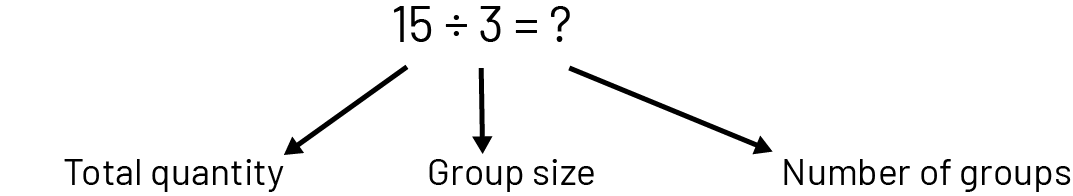
It is essential that both types of problems be addressed, as they are the basis for the integration of other mathematical concepts. It is not necessary for students to know the names of the problem types, but it is essential that they have the opportunity to solve problems of the various types, while employing a variety of strategies.
Source: translated from Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, Numération et sens du nombre, Fascicule 1, Nombres naturels, p. 86.
Written Problems Involving Multiplication and Division
Students develop an understanding of multiplication and division and the relationships between numbers by solving written problems. The types of problems with examples presented below can help students see basic number facts about multiplication and division in a variety of ways. Using problems to introduce basic number facts encourages students to reason their way to solutions and thus develops a better sense of operations.
The written problem examples below contain single-digit numbers. The structures of both types of written problems also lend themselves to multi-digit numbers. The problems are represented using relational rods.
Equal Group Problems
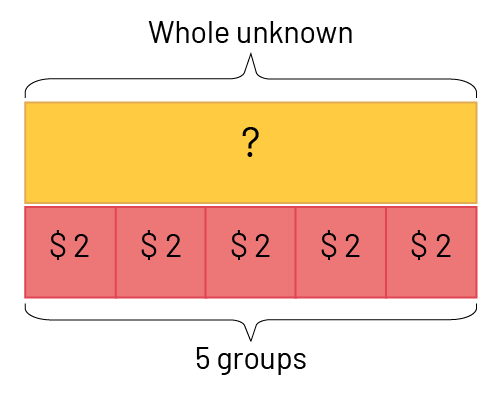
- Equal Groups: Whole Unknown (Multiplication)
Julie bought 5 books for her classmates. Each book cost her $2.00. How much did Julie spend on all these books?
\(2 + 2 + 2 + 2 + 2 = \mathord{?} \) or \(5 \times 2 = \mathord{?} \)
- Equal groups: Number of Groups Unknown (measurement of quotative division)
Julie has bought 10 books for her classmates and is making gift bags. She puts 2 books in each bag. How many gift bags did Julie use?
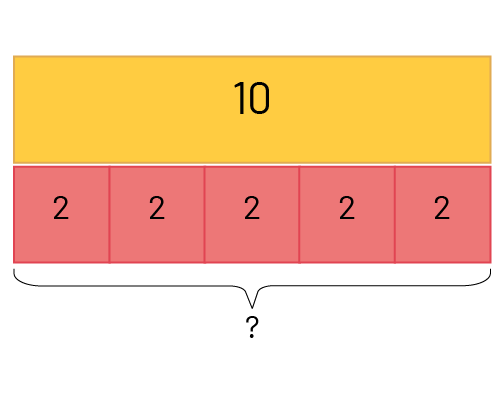

I added 2, 5 times.
or \(10 \div 2 = \mathord{?} \) or \(\mathord{?} \times 2 = 10 \)
- Equal Groups: Group Size Unknown (partitive division)
Julie has 10 books. She wants to give them to 5 of her classmates. How many books will each classmate receive?

\(10 \div 5 = \mathord{?} \) or \(5 \times \mathord{?} = 10 \)
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 6e année, Fascicule 5, p. 10-11.
Inverse Relationship of Division and Multiplication
Similarly, students can develop their understanding that multiplication and division are inverse operations (for example, \(4 \times 5 = 20 \) and \(20 \div 5 = 4 \)). Students can do a variety of activities to develop their understanding of multiplication as repeated addition (for example, \(3 \times 7 \) gives the same result as \(7 + 7 + 7\)) and division as repeated subtractions or repeated additions (for example, \(24 \div 6 \) can be determined by observing that it is possible to perform, from 24, 4 successive subtractions of 6 or that it is possible to carry out, starting from 0, 4 successive additions of 6 to arrive at 24).
Students should engage in various activities to discover the main properties of each of the operations. For example, they can combine 5 sets of 4 cubes and 4 sets of 5 cubes and find that the result is the same (\(5 \times 4 = 4 \times 5 \); commutative property of multiplication). Understanding this property can make it easier to learn basic number facts, among other things.
As students develop an understanding of basic mathematical operations, they are able to use the relationships between these operations to solve problems. For example, to divide 12 pieces of candy equally, they can use a variety of strategies based on any of the operations, such as:
- 2 sets of 6 candies since \(12 \div 6 = 2 \);
- 6 sets of 2 candies since \(6 \times 2 = 12 \);
- 3 sets of 4 candies since 4 candies can be separated 3 times from the set of 12 candies \((12 - 4 - 4 - 4)\) and there will be no candies left;
- 4 sets of 3 candies since \(3 + 3 + 3 + 3 = 12 \).
Source: translated from Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, Numération et sens du nombre, p. 62-63.
Multiplication Strategies
The following is a variety of strategies that can be used to perform multiplication. They meet a variety of needs and facilitate student learning.
Example 1
Amélie's father tells her that her cousin Milène, from Manitoba, is coming to visit soon. Her father has told her that there are 5 weeks left before she arrives. How many days are left until Milène arrives?
one week = 7 days
\(7 \times 5 = \mathord{?} \)
Using the Array Model (Distributive Property)
I decomposed 7 into \(5 + 2 \), and used my (\(5 \times 5\)) + (\(5 \times 2\) ) facts.
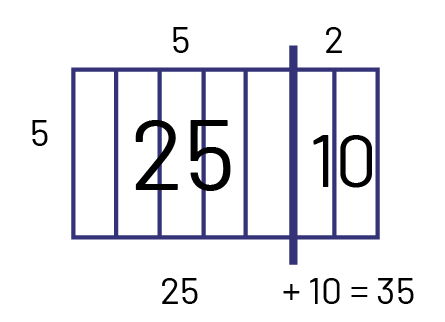
So I can say now that there are 35 days left before Milène arrives.
Example 2
A skateboard has 4 wheels. How many wheels do 8 skateboards have?
\(8 \times 4 = \mathord{?} \)
Strategy 1
Distributive Property by decomposing with a number line
To simplify, I decompose the 8 into \(4 + 4 \). Then I can do the following multiplication: \((4 \times 4) + (4 \times 4)\).
In 4 jumps of 4, I reach 16.

Now that I know that \(4 \times 4 = 16 \), I repeat the operation twice, that is: 16 + 16 = 32.
So, 8 skateboards have 32 wheels.
Strategy 2
Using the Rekenrek (Distributive Property)
I am going to do the multiplication \(4 \times 8 \) with the Rekenrek, because I will have the same result as \(8 \times 4 \). So I will place 8 beads to the left of the Rekenrek on the first 4 rows. I see that there are 4 rods of 5 red beads and 4 rods of 3 white beads. I can calculate these two multiplications more easily now, since 4 groups of 5 beads is \(4 \times 5 = 20 \), and 4 groups of 3 beads is \(4 \times 3 = 12 \).
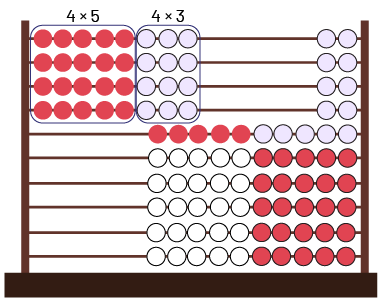
Finally, I just need to add 20 and 12. I combine the tens and then add on the ones \((20 + 10) + 2 = 32\). So there are 32 wheels on 8 skateboards.
Source: L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Example 3
Sylvie buys 6 boxes of cookies. One third of the cookies in each box are peanut butter. How many boxes of cookies are peanut butter?
Problem source: adapted from CFORP, Les mathématiques… un peu, beaucoup, à la folie, Guide pédagogique, Édition révisée, Numération et sens du nombre,3e année, Module 2, Série 2, Minileçon 4 - Des fractions en devinettes, p. 347.
Strategy 1
Repeated Addition Using a Number Line
I know the peanut butter cookies are \(\frac{1}{3}\) of each box and there are 6 boxes in all. So I used repeated addition.
To help me, I represent the 6 leaps of \(\frac{1}{3} \) on a number line.
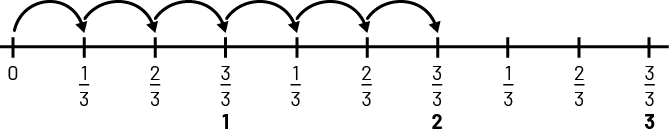
= 6 one thirds or 2 wholes
Strategy 2
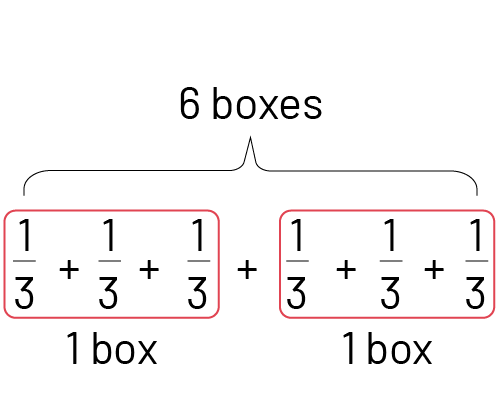
Repeated Addition Using a Diagram
To count the number of thirds, I will represent the 6 one thirds of each box in a diagram.
The first 3 one thirds of peanut butter cookies form 1 whole box. The next 3 one thirds form another whole box. This makes 2 boxes of peanut butter cookies from the 6 boxes of cookies.
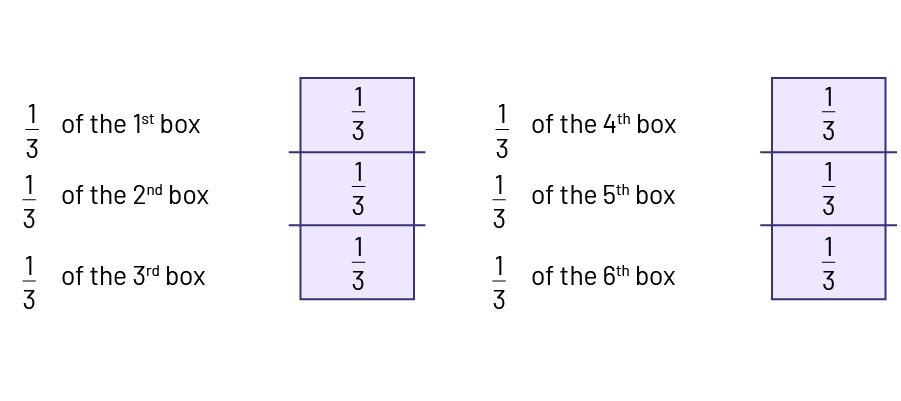
Source: adapted and translated from En avant les maths! 3e, CM, Nombres, p. 5.
Division Strategies
Example 1
It's registration time for swimming lessons. 72 children have registered. The groups are made up of 8 children. How many groups will there be?
Strategy 1
Repeated Subtraction Using the Hundreds Chart
I know that there are a total of 72 children and that the groups are made up of 8 children. I will perform repeated subtractions by representing my groups in a hundreds chart, by putting a circle whenever I make a group of 8.

\(72 - 8 = 64\)
\(64 - 8 = 56\)
\(56 - 8 = 48\)
\(48 - 8 = 40\)
\(40 - 8 = 32\)
\(32 - 8 = 24\)
\(24 - 8 = 16\)
\(16 - 8 = 8\)
\(8 - 8 = 0\)
Now that I've done my repeated subtractions in the hundreds chart, I just need to count the amount of circled numbers that represent the number of groups of children.
I see that there are 9 numbers circled in the hundred chart. There are therefore 9 groups of 8 children.
Strategy 2
Division Using an Array
I made my array by making rows of 8 to represent the groups of children. I know that \(5 \times 8 = 40\), so I made 5 rows. I subtracted 40 from 72, which gave me 32. I know that \(4 \times 8 = 32\), so I add 4 more rows of 8 to get my 72.
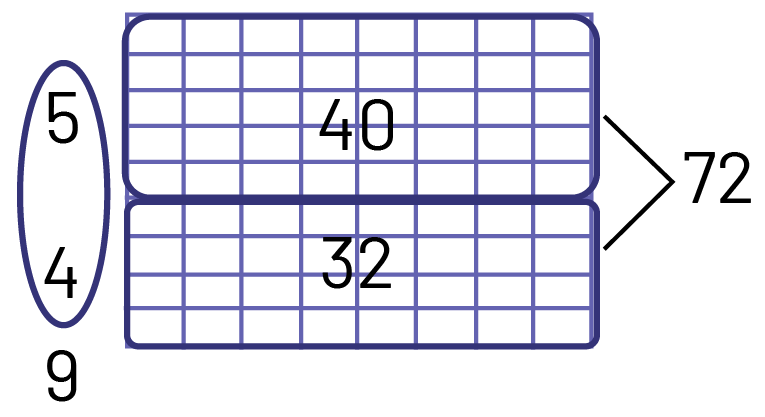
I added the number of rows \(5 + 4 = 9 \). There are 9 groups of 8 children.
Strategy 3
Division Using a Double Number Line
I placed 7 orange relational rods (70) and one red rod (2) above the double number line. This represents the 72 children.
Then I used the brown rods (8) below the line to represent the groups of 8 children. I needed 9 brown rods to reach the total of 72 children.
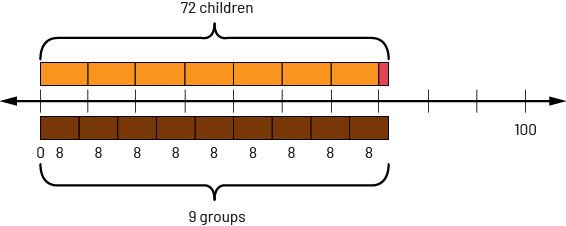
There are 9 groups of 8 children.
Example 2
The teacher hands out one fourth of a sheet of paper to 15 students in her classroom to write a short riddle. How many full sheets of paper did the teacher use?
Strategy
Division using an array and combination
I used the array to represent the 15 students.
I know there are four \(\frac{1}{4} \) in a sheet of paper. I circle four \(\frac{1}{4} \), which gives me a full sheet of paper.

The teacher needs 4 sheets of paper. However, \(\frac{1}{4} \) will remain from the last sheet.
Knowledge: Equal Group Problems
These are problems that involve sets of equal quantity. With these problems, there is a group of a given size, which is repeated a certain number of times to arrive at a result. Sometimes the size of each group is unknown, sometimes the number of groups is unknown, and sometimes the result is unknown.
