B1. Sens du nombre :
Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne.
Situation d’apprentissage 1 : échanges jusqu’à 1 000 (dénombrement)
Durée totale : environ 2 h 30 min
| Attente | Contenus d'apprentissage |
|---|---|
| B1. Sens du nombre démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire, représenter, composer et décomposer les nombres naturels de 0 jusqu’à 1 000, à l’aide d’une variété d’outils et de stratégies, et décrire de quelles façons ils sont utilisés dans la vie quotidienne. B1.4 Compter jusqu’à 1 000, y compris par intervalles de 50, 100 et 200, à l’aide d’une variété d’outils et de stratégies. B1.5 Utiliser la valeur de position pour décrire et représenter des nombres de différentes façons, y compris à l’aide de matériel de base 10. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :
- de compter jusqu’à 1 000 par intervalles de 50, de 100 et de 200 à partir d’un nombre égal ou inférieur à 1 000;
- d’utiliser le concept de valeur de position pour effectuer des regroupements entre les unités, les dizaines et les centaines.
| Contexte pédagogique | Préalables |
|---|---|
| Les activités de dénombrement permettent à l’élève d’approfondir sa compréhension des régularités numériques et des relations entre les nombres. À la fin de la 2e année, l’élève maîtrise les habiletés de base du dénombrement et peut compter jusqu’à 200 par 1 et par intervalles de 2, de 5, de 10, de 20, de 25 et de 50 à partir de divers nombres. En 3e année, l’élève apprend à compter jusqu’à 1 000 par 1 et par intervalles de 50, de 100 et de 200 à partir de divers nombres. Elle ou il doit aussi perfectionner le compte à rebours par intervalles de 2, de 5, de 10 et de 100 à partir d’un nombre égal ou inférieur à 1 000. L’acquisition de stratégies de regroupement par 10 et par 100 lui permet de manier les grands nombres plus facilement. Avec l’utilisation répétée du matériel de base 10, de grilles de nombres et de droites numériques, l’élève devient plus apte à discerner les régularités lors du dénombrement et à percevoir les relations qui existent entre les nombres. | Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Vocabulaire mathématique
compter, compter par intervalles, dizaine, centaine, millier, regrouper, représenter, valeur de position
Matériel
Activité principale
- annexe 3D.1 (Tapis de valeur de position)
- annexe 3D.2 (Échanges jusqu’à 500) (2 copies)
- annexe 3D.3 (Échanges jusqu’à 1 000) (1 copie par équipe de 2)
- matériel de base 10 (2 ensembles)
- dés (4)
- calculatrices (si nécessaire)
Activité supplémentaire
- annexe 3D.1 (Tapis de valeur de position) (1 copie par élève)
- annexe 3D.5 (Objectif 1 000) (1 copie par équipe de 2 ou 4)
- jetons de couleur différente (4 par équipe de 2 ou 4)
- dés (1 par équipe de 2 ou 4)
- cartes de nombre de 1 à 9 (1 jeu par équipe de 2 ou 4)
- matériel de base 10 (1 ensemble par équipe de 2 ou 4)
Avant l’apprentissage (mise en train)
Durée : environ 50 minutes
Échanges jusqu’à 500
Diviser la classe en 2 équipes : A et B.
Remettre à chaque équipe une copie des annexes 3D.1 et 3D.2, du matériel de base 10 et 2 dés numérotés de 1 à 6.
Préciser que le but du jeu est d’être la 1re équipe à atteindre 500, sans dépasser ce nombre et que chaque équipe commence à compter à partir de son nombre de départ par 1 ou par intervalles de 10, de 100.
Leur demander de déterminer le nombre de départ en lançant les 2 dés. Les nombres obtenus composent le nombre de départ. À titre d’exemple, si une équipe a obtenu un 2 et un 4 en lançant les dés, elle peut choisir 24 ou 42 comme nombre de départ.
Inviter un membre de l’équipe à utiliser le matériel de base 10 pour représenter le nombre de départ sur le tapis de valeur de position. Par exemple, si le nombre choisi est 42, l’élève dépose 4 languettes dans la colonne des dizaines et 2 cubes d’unité dans la colonne des unités.
Expliquer les règles du jeu :
- Un membre de l’équipe A lance un dé. Le nombre obtenu correspond au nombre de fois que l’équipe peut compter lorsque c’est à son tour de jouer. L’équipe décide aussi, après chaque lancer du dé, si elle compte par 1 ou par intervalles de 10 ou de 100. Par exemple, si le nombre de départ de l’équipe est 23 et qu’elle a obtenu le nombre 3, l’équipe peut compter 3 fois à partir de 23 selon l’intervalle qu’elle a choisi : par 1 (24, 25, 26), par intervalles de 10 (33, 43, 53) ou par intervalles de 100 (123, 223, 323).
- Pendant que l’équipe A compte à partir de son point de départ, un ou une élève ajoute du matériel de base 10 sur le tapis de valeur de position.
- Pendant le jeu, les élèves effectuent les échanges en remplaçant 10 cubes d’unité par une languette ou 10 languettes par une planchette.
- À chaque tour, l’équipe note ses résultats sur la copie de l’annexe 3D.2.
Exemples
Pour effectuer 3 bonds par intervalles de 100 à partir de 23, les élèves noteraient ce qui suit :

Pour effectuer 4 bonds par intervalles de 10 à partir de 323, les élèves noteraient ce qui suit :
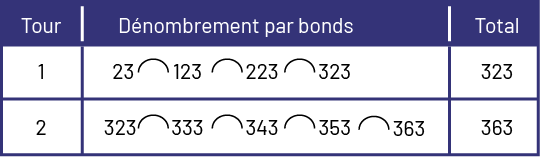 Image Tableau qui permet de noter le numéro du tour, le dénombrement par bonds et le total. Pour le tour un, 23, un bond, 123, un bond, 223, un bond, 323, total 323. Pour le tour 2, 323, un bond, 333, un bond, 343, un bond, 353, un bond, 363, total 363.
Image Tableau qui permet de noter le numéro du tour, le dénombrement par bonds et le total. Pour le tour un, 23, un bond, 123, un bond, 223, un bond, 323, total 323. Pour le tour 2, 323, un bond, 333, un bond, 343, un bond, 353, un bond, 363, total 363.
Le jeu se poursuit ainsi, chaque équipe comptant à partir du nombre indiqué sur le tapis de valeur de position. Lorsqu’elles se rapprochent du nombre 500, les équipes peuvent passer leur tour si le nombre indiqué par le dé est trop élevé. Par exemple, l’équipe qui a atteint le nombre 496 et qui obtient le nombre 6 en lançant le dé a avantage à passer son tour, car elle dépasserait 500.
S’assurer que tous les membres de l’équipe participent au jeu en alternant les rôles chaque fois que le dé est lancé (par exemple, le 1er élève lance le dé, le 2e ajoute du matériel de base 10 sur le tapis de valeur de position, le 3e inscrit les résultats, le 4e lance le dé, le 5e place le matériel de base 10 et ainsi de suite).
Rassembler les équipes une fois le jeu terminé et poser les questions suivantes :
- Quelles stratégies de regroupement avez-vous utilisées au cours de ce jeu?
- Quand est-il préférable de compter par 1? par intervalles de 10? de 100?
- En quoi le matériel de base 10 est-il utile pour jouer à ce jeu?
- Quelles régularités avez-vous constatées pendant que vous comptiez par intervalles de 10? de 100?
Pendant l’apprentissage (exploration)
Durée : environ 50 minutes
Jouer au jeu des échanges jusqu’à 1 000 et appliquer les mêmes règles que celles du jeu précédent, mais les équipes cherchent à atteindre 1 000 et à « gagner » le cube de millier.
Grouper les élèves en équipes de 4. Elles et ils joueront 2 contre 2.
Distribuer 2 copies de l’annexe 3D.3 (Échanges jusqu’à 1 000) à chaque équipe et demander d’y inscrire leurs résultats.
Circuler pendant le jeu. Écouter les élèves et observer les stratégies qu’elles et ils utilisent.
Poser des questions pour les amener à verbaliser leur démarche telles que :
- Pourquoi avez-vous décidé de compter par intervalles de 100 cette fois-ci?
- Qu’est-ce qui serait arrivé si vous aviez compté par intervalles de 200?
- Quelle stratégie de regroupement utilisez-vous?
- Pourquoi avez-vous besoin de faire un échange de matériel de base 10 à ce moment-ci?
Après l’apprentissage (objectivation/transfert de connaissances)
Durée : environ 50 minutes
Rassembler les élèves et poser les questions suivantes :
- Qu’est-ce qui était difficile dans ce jeu?
- Quelles stratégies de regroupement avez-vous utilisées pendant le jeu?
- Qu’avez-vous remarqué en comptant par intervalles de 100 et de 200?
- Qu’avez-vous remarqué en utilisant du matériel de base 10?
- Que remarquez-vous lorsque vous effectuez les différents bonds?
- Quelles régularités avez-vous observées?
Demander aux élèves de noter, individuellement ou en équipe de 2, leurs réflexions dans leur journal de mathématiques. Proposer quelques exemples de phrases à compléter pour faciliter le travail.
Exemples
- Le matériel de base 10 m’a été utile aujourd’hui parce que…
- Pendant le jeu, j’ai…
- Si j’avais un conseil pratique à donner à une personne qui joue pour la 1re fois, je lui dirais…
- J’ai repéré les régularités suivantes lorsque je comptais par intervalles de 100 et de 200 :… (par exemple, le chiffre des centaines augmente toujours de 1 ou de 2; le chiffre des dizaines et celui des unités demeurent toujours les mêmes)
- Quand j’ajoute 100 à un nombre comme 230 ou 340, je remarque que…
- Quand j’ajoute 200 à un nombre comme 364 ou 287, je remarque que…
Exemples de critères d’évaluation
L’élève :
- compte par intervalles de 50 à partir de n’importe quel point de départ.
- compte par intervalles de 100 à partir de n’importe quel point de départ.
- compte par intervalles de 200 à partir de n’importe quel point de départ.
- décrit les régularités lorsque l’élève compte par intervalles de 50, de 100 et de 200.
- échange des unités contre des dizaines au moment opportun.
- échange des dizaines contre des unités ou des centaines au moment opportun.
- échange des centaines contre des dizaines ou des milliers au moment opportun.
Activité supplémentaire
Objectif 1 000
Grouper les élèves par 2 ou 4.
Remettre une copie de l’annexe 3D.1 à chaque élève.
Distribuer une copie de l’annexe 3D.5, 4 jetons de couleur différente, 1 dé, 1 jeu de cartes de nombre de 1 à 9 et du matériel de base 10 à chaque équipe.
Demander aux élèves de se choisir un jeton et de le placer sur la case de départ.
Expliquer les règles du jeu :
- L’élève A lance le dé ou tire une carte pour déterminer sur combien de cases l’élève peut déplacer son jeton.
- L’élève fait le total des nombres sur lesquels son jeton s’est déplacé. Par exemple, si l’élève obtient 5 en lançant le dé, en partant de la case de départ, l’élève déplace son jeton sur 5 cases, soit les cases 20, 40, 50, 90 et 60. L’élève additionne ces nombres, soit \(20 + 40 + 50 + 90 + 60 = 260\).
- L’élève représente le total des points sur le tapis de valeur de position (annexe 3D.1) à l’aide du matériel de base 10.
- Les autres élèves répètent les mêmes étapes à tour de rôle.
- L’élève qui atteint 1 000 le 1er ou la 1re gagne.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 177-184.
Situation d’apprentissage 2 : estimation du nombre (quantité)
Durée totale : environ 2 heures
| Attente | Contenus d'apprentissage |
|---|---|
| B1. Sens du nombre démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire, représenter, composer et décomposer les nombres naturels de 0 jusqu’à 1 000, à l’aide d’une variété d’outils et de stratégies, et décrire de quelles façons ils sont utilisés dans la vie quotidienne. B1.3 Arrondir les nombres naturels à la dizaine et à la centaine près, dans divers contextes. B1.4 Compter jusqu’à 1 000, y compris par intervalles de 50, 100 et 200, à l’aide d’une variété d’outils et de stratégies. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :
- d’estimer des nombres de plus en plus grands;
- de se donner des stratégies d’estimation;
- d’utiliser l’estimation pour résoudre des problèmes de la vie courante.
| Contexte pédagogique | Préalables |
|---|---|
|
L’estimation est un des aspects importants du sens du nombre. Dans la vie de tous les jours, qu’il s’agisse d’évaluer la valeur de quelques achats à l’épicerie, la masse d’un objet ou une distance à parcourir, on utilise plus fréquemment des réponses approximatives que des réponses exactes. C’est pour cette raison que l’on doit continuer à développer le concept de quantité chez l’élève et à améliorer la précision de ses estimations. En 3e année, l’élève peut estimer de grandes quantités, mais en l’absence de points de repère, ses estimations risquent de ne pas être vraisemblables. Un point de repère est une quantité connue et comprise. Connaître la quantité que représente un point de repère permet d’explorer ou d’estimer une quantité plus grande. Par exemple, si on sait qu’une poignée contient environ 10 bonbons, on peut estimer qu’un pot de bonbons contient environ 6 poignées, soit 60 bonbons. C’est par le biais d’activités répétées de ce genre que l’élève parvient à comprendre que l’utilisation de points de repère, ainsi que le raisonnement lié au concept de proportionnalité, permet d’obtenir une estimation juste. |
Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Vocabulaire mathématique
estimer, estimation, arrondir, point de repère, stratégie, nombre réel, vraisemblable, plus que, moins que, près de, un plus grand nombre, un moins grand nombre
Matériel
- annexe 3Q.1 (a) (Estime la quantité) (1 copie par élève)
- annexe 3Q.1 (b) (Estime la quantité) (1 copie par élève)
- annexe 3Q.2 (Qu’est-ce qu’on mange?) (1 copie par élève)
- récipients transparents contenant de petits objets (1 par équipe de 3 ou 4)
- calculatrices (au besoin)
- grande feuille de papier ou tableau interactif
Avant l’apprentissage (mise en train)
Durée : environ 40 minutes
Plusieurs activités d’estimation de quantité exigent qu’après l’estimation, les élèves déterminent le nombre réel en dénombrant.
En général en 3e année, elles et ils ne veulent plus estimer une réponse puisqu’elles et ils doivent de toute façon vérifier leurs solutions. Par conséquent, il faut leur démontrer l’importance d’estimer, c’est-à-dire d’être capable de voir si une réponse est vraisemblable ou non.
Amorcer une discussion pour amener les élèves à réfléchir aux nombres à l’aide des questions suivantes :
- Pour vous, qu’est-ce qu’un grand nombre?
Note : Tout nombre difficile à estimer peut être considéré comme étant un grand nombre (par exemple, 50).
- Où avez-vous vu de grands nombres? Que représentaient-ils? (par exemple, prix des autos chez un concessionnaire)
- Quels objets trouve-t-on en grande quantité? (par exemple, produits en vrac)
- Comment peut-on dénombrer les objets qu’on trouve en grande quantité?
Inscrire les idées des élèves au tableau interactif ou sur une grande feuille de papier.
Placer sur une table plusieurs récipients contenant au moins 200 petits objets (par exemple, jetons, cubes emboîtables, macaronis, attaches de sacs à pain, billes).
Présenter le problème suivant :
« J’ai trouvé ces récipients dans une armoire de la classe et j’aimerais savoir combien d’objets chacun contient. J’ai besoin de votre aide pour estimer la quantité d’objets dans chaque récipient. »
Former des équipes de 3 ou 4 et remettre un récipient à chacune.
Demander aux élèves d’estimer le nombre d’objets contenus dans le récipient.
Spécifier que chaque équipe doit choisir une stratégie qui l’aidera à faire l’estimation la plus juste possible.
Souligner que dénombrer tous les objets ne peut pas être considéré comme une stratégie d’estimation.
Accorder suffisamment de temps pour que les élèves aient la possibilité de réfléchir à la question et de discuter de la meilleure stratégie à utiliser.
Demander aux équipes de noter leur estimation, d’appliquer leur stratégie et de dénombrer ensuite tous les objets pour vérifier dans quelle mesure la quantité estimée se rapproche de la quantité réelle.
Observer les élèves au travail et vérifier si leurs stratégies d’estimation et de dénombrement sont efficaces.
Rassembler les élèves pour la mise en commun. Inviter les équipes à venir, à tour de rôle, montrer leur récipient d’objets et à demander aux autres élèves d’en estimer la quantité.
Demander à un membre de l’équipe d’expliquer la stratégie d’estimation utilisée (par exemple, avoir un point de repère, arrondir, grouper les objets), de révéler l’estimation et de dévoiler le nombre réel d’objets dans le récipient.
Vérifier, à main levée, combien d’élèves étaient à 5, à 10, à 20, à 30,… du nombre réel.
Demander aux élèves d’identifier les stratégies d’estimation qui semblent donner les meilleurs résultats et d’expliquer pourquoi.
Discuter de l’utilisation de points de repère et du fait qu’ils permettent de faire des estimations plus justes.
Mettre l’accent sur le fait que faire une estimation ne signifie pas « déterminer la quantité exacte », mais « déterminer la quantité la plus près possible de la quantité réelle ».
Pendant l’apprentissage (exploration)
Durée : environ 50 minutes
Discuter de situations où il convient de faire une estimation à l’aide des questions suivantes :
- Quand et pourquoi fait-on des estimations dans la vie de tous les jours?
- Parlez-moi d’une situation où vous avez fait une estimation.
- Que se passerait-il si on sous-estimait ou surestimait les quantités d’aliments à acheter pour le pique-nique de l’école?
Lire les livres suivants et discuter des stratégies d’estimation utilisées : Célébrons de 100 façons, Cinq à la fois, Plus ou moins vingt, coll. « Chenelière mathématiques ».
Grouper les élèves en équipes de 2 ou 3.
Remettre une copie de l’annexe 3Q.1 (a) et 1 (b) à chaque élève et leur demander de résoudre les problèmes.
Rappeler l’importance de se donner des points de repère comme stratégie afin de faire des estimations justes.
Après l’apprentissage (objectivation/transfert de connaissances)
Durée : environ 30 minutes
Inviter chaque équipe à présenter un problème et à expliquer la stratégie utilisée pour le résoudre.
Inscrire toutes les stratégies au tableau interactif ou sur une grande feuille de papier.
Voici quelques stratégies possibles :
- utilisation d’un point de repère (par exemple, comme dans Célébrons de 100 façons);
- utilisation de « beaux » nombres, c’est-à-dire de nombres faciles à manier (par exemple, utiliser 20 au lieu de 23);
- addition répétée ou dénombrement (par exemple, comme dans Cinq à la fois);
- arrondissement à la dizaine ou à la centaine près;
- utilisation de matériel de manipulation (par exemple, comme dans Plus ou moins vingt);
- multiplication.
Poser des questions pour permettre aux élèves de réfléchir à leur démarche :
- Quelle autre stratégie d’estimation auriez-vous pu utiliser?
- Est-ce que vos estimations étaient vraisemblables?
- Est-ce que le nombre 10 (1 000, 256) aurait pu être une estimation acceptable? Pourquoi?
Exemples de critères d’évaluation
L’élève :
- explique la différence entre estimer et dénombrer;
- justifie les raisons pour lesquelles son estimation est près ou éloignée du nombre exact;
- établit un point de repère et l’utilise pour faire son estimation;
- applique des stratégies efficaces d’estimation;
- justifie la vraisemblance d’une estimation.
Différenciation pédagogique
La situation d’apprentissage peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
| Commencer par faire estimer des quantités inférieures à 100 objets. |
|
Suivi à la maison
Qu’est-ce qu’on mange?
À la maison, l’élève peut estimer par exemple :
- le nombre de petites ou de grosses guimauves qu’il y a dans 6 tasses;
- le nombre de macaronis que contiennent 2 tasses;
- la quantité d’ingrédients nécessaires pour cuisiner un plat (par exemple, la quantité de spaghettis requise pour un repas familial) en ayant comme point de repère la quantité que mange une personne;
- le nombre de biscuits ou de crêpes que l’élève peut faire à partir d’un bol de pâte.
Distribuer une copie de l’annexe 3Q.2 à chaque élève pour que l’élève puisse faire l’activité sous la surveillance d’un membre de sa famille.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 193 à 198.
